Bar Magnet
Main Idea
Permanent magnets are objects made of a material which produces its own persistent magnetic field. A bar magnet is a type of permanent magnet which is in the shape of a rectangular prism having two magnetic poles, one on either side. In a bar magnet, the magnetic dipole moment vector points from the South pole to the North pole, while the magnitude of the vector depends on the strength of the magnet. The magnetic field of a bar magnet is exactly that of any other dipole, where the lines of magnetic field curl around from the North pole to the South pole. Unlike electric dipoles, the individual magnetic monopoles of a magnetic dipole cannot be separated. If you were to cut a bar magnet in half, you would simply have 2 smaller bar magnets. A magnetic monopole has never been observed.
A magnetograph can be created by placing a piece of paper over a magnet and sprinkling the paper with iron filings. We can use this to visualize the magnetic field induced by a bar magnet. The particles align themselves with the lines of the magnetic field produced by the magnet. The lines show where the magnetic field exits the material at one pole and re-enters the material at the other pole. It should be noted that the magnetic lines exist in three dimensions, but are only seen in two dimensions in the image.

The main idea for this topic is to explore the physical properties of bar magnets and how they interact with the environment. The magnetic field produced by a bar magnet, as explained above, is strongest inside the magnet itself. The external location where the field is the strongest is just outside the poles, on axis. A practical way to observe this phenomenon (shown mathematically below) is using a compass, which being magnetized itself, will point it's North end towards the South pole of any permanent magnet (including the Earth itself! The 'North' pole of the Earth is actually a type S pole), therefore, moving a compass around a bar magnet will accurately illustrate the direction of the net magnetic field vector at any point. Subtracting Earth's magnetic field (varying from 2.5E-5 T to 6.5E-5 T on Earth's surface) will give the direction of the magnetic field of the bar magnet.
There are two different types of Bar Magnets:
- 1. Alnico Bar Magnets
- The primary components of Alnico magnets are aluminum, nickel, cobalt, and iron. These magnets produce a strong magnetic field and retain their magnetic property even under extreme heat.
- 2. Neodymium Bar Magnets
- Neodymium bar magnets are made with a mixture of neodymium, boron, and iron. These are both extremely powerful and very brittle magnets.
Both of these magnets are magnetized by a phenomenon called ferromagnetism. Unfortunately, ferromagnetism requires quantum mechanics to explain fully, but can be simply explained as the tendency of ferromagnetic materials to align the tiny magnetic dipoles produced by atomic particles, summing to produce a much stronger magnetic dipole moment in the material as a whole.
Mathematical Model
In physics, it is important to keep track of your frame of reference. Treat an effect as if it is arising at the source location and ending at the observation location. The source location marks the beginning point for an effect. The result of the effect is gauged at the observation location.
Due to the fact that an observation location can either be on the axis of the magnet, or off the axis of the magnet, we have two different equations. Given a bar magnet with magnetic dipole moment [math]\displaystyle{ \mu }[/math]:
- If the observation location is on the same axis as the magnet, assuming that the distance from the observation location to the magnet is much greater than the separation distance of the two poles [math]\displaystyle{ (r \gt \gt s) }[/math], we find that:
- [math]\displaystyle{ B = \frac{\mu _{0}}{4\pi }\frac{2\mu }{r^{3}} }[/math]
- If the observation location is on the perpendicular axis of the bar magnet, and assuming that the distance from the observation location to the magnet is much greater than the separation distance of the two poles [math]\displaystyle{ (r \gt \gt s) }[/math], we conclude that:
- [math]\displaystyle{ B = \frac{\mu _{0}}{4\pi } \frac{\mu }{r^{3}} }[/math]
Computational Model

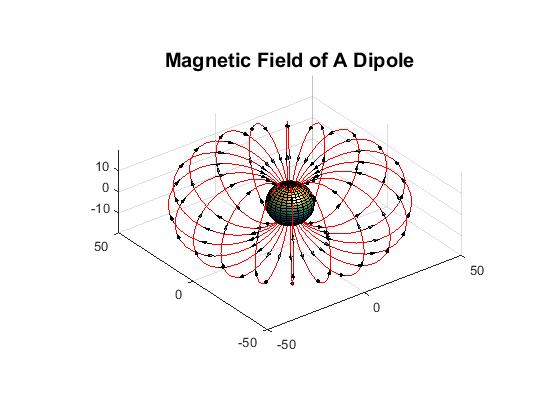
As you can see in this picture, the magnetic field of a bar magnet takes the exact same form as the electric field of a dipole. The magnetic field lines flow out of the North pole of the magnet, and into the South pole of the magnet, in a curving fashion. However, the 'poles' are merely just conventions. They do not represent anything, and are terms assigned to each end. However, it is true that the magnetic field will always flow out of the 'North' end.
Computationally, creating a magnetic dipole is challenging because we cannot use the Law of Superposition to represent it. Instead we must use a ring of current, which produces a dipole field to approximate it. The following code snippet is part of a program which creates a 3D model of a magnetic dipole's field:
function hh=lforce3d(n,clr)
% Lforce3D
d2r = pi/180; r2d=1/d2r;
tht=d2r*(0:5:360)';
phi=d2r*(0:ceil(180/n):180);
hh=phi*r2d;
A=50;
r=A*sin(tht).^2;
rho=r.*sin(tht);
x=rho*cos(phi);
y=rho*sin(phi);
[nR,nC]=size(x);
u=ones(1,nC);
z=r.*cos(tht)*u;
% Draw Line of Force
h = figure;
plot3(x,y,z,'r');
hold on;
axis equal
% Draw The Earth's Spheroid
[u,v,w]=sphere(25);
surf(10*u,10*v,9*w);
colormap('default');
camlight right;
lighting phong;
Examples
Simple
A bar magnet is located at the origin of the xy-plane, with its North end aligned with the positive x-axis.
- a) What are the directions of the magnetic field at the following observation locations? Above the magnet, Below the magnet, To the Left of the magnet, To the Right of the magnet, and In a Plane Above the magnet [math]\displaystyle{ (+z) }[/math].
- We know the magnet field of a bar magnet flows from the North Pole to the South Pole in curves.
- Above:
- Below:
- Left:
- Right:
- Plane Above:
Middling
A bar magnet with a magnetic dipole moment [math]\displaystyle{ \mu = 0.58 \text{ A} \cdot \text{m}^2 }[/math] lies on the [math]\displaystyle{ -x }[/math] axis. A compass is located at the origin. Magnetic North is in the [math]\displaystyle{ -z }[/math] direction. Between the bar magnet and the compass is a coil of wire of radius [math]\displaystyle{ R = 3.5 \text{ cm} }[/math]. The distance from the center of the coil to the center of the compass is [math]\displaystyle{ d_{cc} = 9.6 \text{ cm} }[/math]. The distance from the center of the bar magnet to the center of the compass is [math]\displaystyle{ d_{bc} = 23.0 \text{ cm} }[/math]. A steady current of [math]\displaystyle{ 0.96 \text{ A} }[/math] runs through the coil. The conventional current runs clockwise in the coil when viewed from the location of the compass (the origin). Despite the presence of the magnet and coil, the compass still points north.
- a) Which pole of the bar magnet is closer to the compass?
- b) How many turns of wire are in the coil?
Difficult
We already know that the field of a bar magnet flows out of the North end and into the South end in a curving fashion. So, using the diagram above, it is easy to see that to the right of the magnet, the direction of the magnetic field points in the +X direction. At a position to the left of the magnet, the field is flowing back into the south end of the magnet, so the direction of the magnetic field at this location is also in the +X direction.
The field above and below the magnet is flowing from the right to the left at both locations, so the direction of the magnetic field above and below the magnet is in the -X direction.
At a different plane (z ≠ 0), there is no magnetic field, because we can assume that bar magnet acts as a 2-D dipole.
Example 2:
Part A: Because the conventional current runs clockwise in the coil, you can use right hand rule to determine what direction the magnetic field is due to the coil. This tells us that the magnetic field due to the coil is in the -X direction. In order for the compass to stay still, the magnet needs to directly oppose the magnetic field of the coil, meaning its magnetic field has to point in the +X direction, meaning the north pole would have to be nearer the compass.
Part B: Because the magnetic field created by the coil is equal to the magnetic field created by the magnet, we can set their two fields equal to each other: [math]\displaystyle{ \frac{\mu _{0}}{4 \pi } \cdot \frac{2\mu }{r^{3}} = \frac{\mu _{0}}{4 \pi } \cdot \frac{2NI\pi R^{2}}{(z^{2}+R^{2})^{3/2}} }[/math]
Rearranging to solve this equation for N, we get: [math]\displaystyle{ N = \frac{\mu (z^{2}+R^{2})^{3/2}}{I\pi R^{2} d^{3}} }[/math]
Plugging in .58 A∙m2 (the magnetic dipole moment, μ), .096 meters for z, .035 meters for R, .96 Amps for I, and .23 meters for d, we get that the number of loops in the coil is 14.
Connectedness
[[File:Series L0.JPG|thumb|left|An experimental MAGLEV train created by Japanese engineers.

One very interesting applications of magnets is their ability to levitate objects. This is the main driving force in the case of MAGLEV trains. Magnetic levitation, or MAGLEV trains, hover above a long series of magnets where the magnets on the bottom of the train repel the magnets on the tracks below it. Sending an electric current through the coils on the bottom of the track allows the train to levitate a few inches off the ground, and propelling the current through the guided coils on the bottom of the track propels the train forward at unbelievable speeds (up to 250 MPH)!
Making the train levitate is a useful tool because it reduces the amount of friction between the wheels and the track, allowing for much more efficiency overall.
Magnetism is also used in medical technology. Medical Resonance Imaging (MRI) machines use magnetic fields and radio waves to create images of the body.
History

The first magnets were not invented, but rather discovered. The ancient Greeks and ancient Chinese stumbled upon a naturally occurring material, called magnetite, by mistake. People were so astounded by it that tales were told of magical islands where magnetic nature was everywhere. The Chinese actually developed a compass around 4500 years ago using this magnetite!
Despite not being the first people to study magnetism, Hans Christian Oersted did prove that electricity and magnetism were related by bringing a current carrying wire close to a compass needle. However, it wasn't until Maxwell published his findings in 1862 that led to the relationships between electricity and magnetism (Maxwell's Equations; see other Wikipedia page).
Bar magnets have been used for years to show magnetic fields and magnetic lines of force. An example of this is to pour metal filings onto a piece of paper that is suspended above a magnet. As time goes on, the shavings will align themselves into arcs that go outward from the magnet’s south and north poles. A second example would be that it involves trying to touch the north poles of two different weak magnets together to show how the poles repel against each other. Splitting a bar magnet in half will obviously create two magnets. Each of those two different magnets will have a north and south pole. However, we must be careful. Excessive force or heat from cutting can demagnetize the bar.
See also
External links
- MAGLEV Trains: http://www.scienceclarified.com/everyday/Real-Life-Physics-Vol-3-Biology-Vol-1/Magnetism-Real-life-applications.html
- More information on Bar Magnets: http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/elemag.html