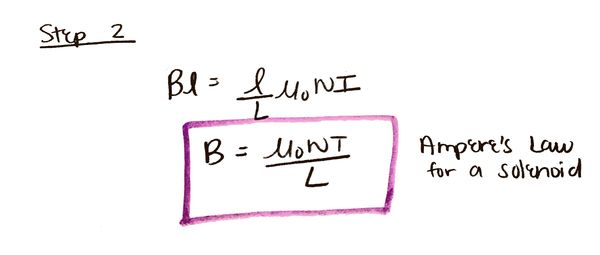Magnetic Field of a Solenoid Using Ampere's Law

Improved by Miranda Harmon Spring 2018

This page explains how to use Ampere's Law to solve for the magnetic field of a solenoid, and the derivation of the formula of the magnetic field of a solenoid.

The Main Idea

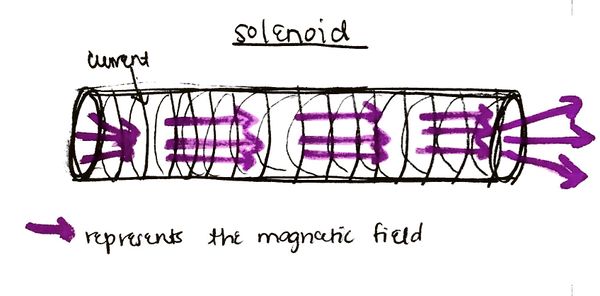
A solenoid is a cylindrical coil of wire that produces a uniform magnetic field when it is carrying an electric current. This is similar to the magnetic field generated by a bar magnet. A solenoid is a form of an electromagnet that can create strong controlled magnetic fields throughout the coil except at the ends.The magnetic field of solenoid can be solved by using Ampere's Law equation which relates the magnetic field surrounding the solenoid and the electric current. The magnetic field inside of the solenoid is directly proportional to the number of turns in the coil, as well as the applied current running through the wire.

Looking at the model, in the middle of the solenoid the field is constant throughout the entirety of the interior and is parallel to the axis. At the ends of a solenoid the magnetic field starts to point outward at varying angles. The greater the current and the more turns in the coil per unit, the greater the field inside the solenoid. Ideally, a perfect solenoid would have have a uniform magnetic field on the inside, and zero magnetic field on the outside.

Equation

Ampere's Law gives us the form:

[math]\displaystyle{ {\oint\,\vec{B}•d\vec{l} = μ_{0}∑I_{inside path}} }[/math]

If there are [math]\displaystyle{ N }[/math] loops of wire that compose a solenoid of length [math]\displaystyle{ L }[/math], we can begin by replacing [math]\displaystyle{ d\vec{l} }[/math] with [math]\displaystyle{ L }[/math] because that is the length of the solenoid.

We can then solve for [math]\displaystyle{ B }[/math]:

[math]\displaystyle{ {B = \frac{μ_{0}NI}{L}} }[/math]

It is important to note the reason we are multiplying by N. When we solve for the magnetic field of a solenoid, we are only solving for the magnetic field of one of the coils. When we multiply by N, which is the number of coils in the solenoid, we are now able to state the total magnetic field of the solenoid.

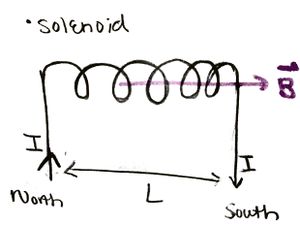
The Right-Hand Rule can be used to find the direction of the magnetic field. Begin by taking your right hand and curling it around the coil in the direction of the current. Stick your thumb straight out, and it should be pointed in the direction of the magnetic field due to the coil. Keep in mind that the direction of the magnetic field will lie on the same axis as the length of the solenoid.

The Right-Hand Rule can also be used when we are given the magnetic field for the coil, and we need to find the current. To find the current, point your thumb in the direction of the magnetic field. The direction that your fingers wrap around is the direction that conventional current is moving around the coil. This idea can be seen demonstrated below.

Derivation of Equation

Looking at the equation of a solenoid, it could be difficult to understand how this equation was derived. Listed below are the steps that are taken to derive the equation and an image depicting what each symbol represents.

Steps to Derive Equation:

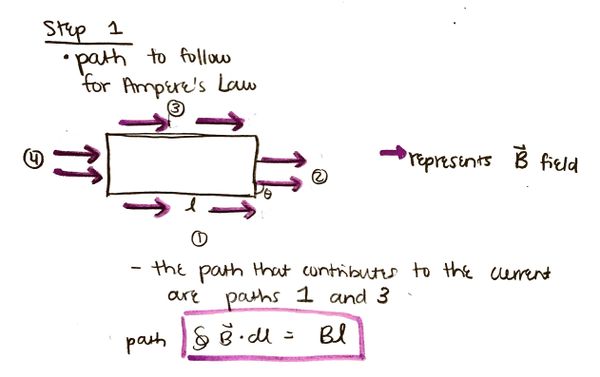
1. Apply Ampere's law by finding the formula for relating the path of the current and magnetic field: [math]\displaystyle{ {\oint\,\vec{B}•d\vec{l}} }[/math].

2. Find that Ampere's law is proportional to the path and solenoid's length proportionality times the number of turns in the solenoid and the electric current: [math]\displaystyle{ {Bl = \frac{μ_{0}NIl}{L}} }[/math].

3.Cancel out the length of the path on each side of the equal sign to get the equation we use: [math]\displaystyle{ {B = \frac{μ_{0}NI}{L}} }[/math]

Drawing of the solenoid

Ampere's law is proportional to the path and solenoid's length proportionality times the number of turns in the solenoid and the electric current. It is important to note that after step 1, we canceled out the dot product between the magnetic field and current.The dot product is used in order to use the portion of the magnetic field that is in the direction of [math]\displaystyle{ d\vec{l} }[/math]. However, we should notice that since our magnetic field is following the path of the circle, magnetic field and the length of the field are parallel. Thus, the dot product is not needed due to the fact that the two components are already moving in the same direction.

Cancel out the length of the path on each side of the equal sign to get the equation we use

Symbols:

l:the length of the rectangular path decided to take to the length apply Ampere's Law

L:the length of the solenoid

B: the magnetic field of the solenoid

N: the number of turns in the solenoid

μ_0: a constant

I: conventional current flowing through the solenoid

Examples

Solving for the Magnetic Field

Find the magnetic field produced by a 20 cm long solenoid if the number of loops is 200 and current passing through it is 8 A.

For this example all of the variables are given so it is just a simple math calculation using Ampere's Law, as given above, but for reiteration.

[math]\displaystyle{ {\oint\,\vec{B}•d\vec{l} = μ_{0}∑I_{inside path}} }[/math]

[math]\displaystyle{ {B = \frac{200*8}{.2}} }[/math] [math]\displaystyle{ {B = 8,000} }[/math]

Once you have solved for [math]\displaystyle{ B }[/math] all you have to do is find the direction of the magnetic field using the Right Hand Rule.

Must convert 20 cm to .2 m

For more practice of calculating the magnetic field of a solenoid, it is best to practice homework and practice problems, as well as looking over examples from class notes.

Solving for the Current

A solenoid has a magnetic field of 6x10^-4 T, 2000 turns, and is 10 cm long. What is the current through the solenoid? For this example you are solving for I. Very similar to the above question, just rearranging the calculation of Ampere's Law.

[math]\displaystyle{ {I = \frac{LB}{μ_{0}N}} }[/math]

[math]\displaystyle{ {I = \frac{.1*6E-4}{2000}} }[/math] [math]\displaystyle{ {I = 3E-8 A} }[/math]

Must change 10 cm to .1 for the cm to m conversion

Connectedness

Solenoids are important because they can create controlled magnetic fields making them useful for a variety of applications.
As a mechanical engineering major solenoids are relevant to my major because mechanical engineers use solenoid components, and solenoid valves on a daily basis. An example of solenoids is a transformer which consists of a solenoid with different induced electric currents and number of turns which can perform step down or step up functionalities.
Solenoids can be used to make a small current that can switch a much larger current. For example, the starter in a washer or dryer is flipped on by the small current of a solenoid.

History

Andre - Marie Ampere developed the Ampere Law equation by experimenting with bar magnets. He found that If he passed an electric current through a wire, a magnetic field is created. Ampere found that sometimes a magnet attracted another magnet, but at other times, they repelled each other. Then he found that this attraction or repulsion depends on the direction that current is flowing in the wire and in what orientation the magnets are being held. By trying different experiments and different equations, he gradually found that this equation(Ampere's Law) could be used to calculate the results he found in this experiment. Ampere was also the founder of creating the solenoid, and therefore used Ampere's Law to define the relationship between the solenoid's magnetic field to the current in the solenoid.

Magnetic Field of a Solenoid Using Ampere's Law

Contents

The Main Idea

Equation

Derivation of Equation

Examples

Solving for the Magnetic Field

Solving for the Current

Connectedness

History

See Also

Further Reading

External Links

References

Navigation menu