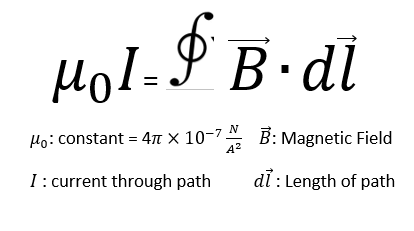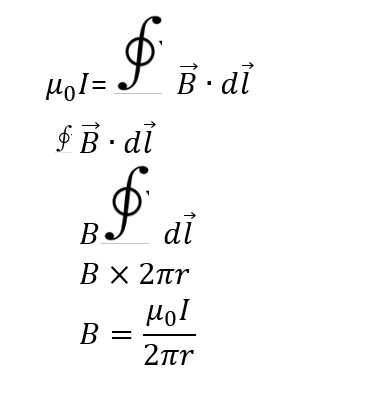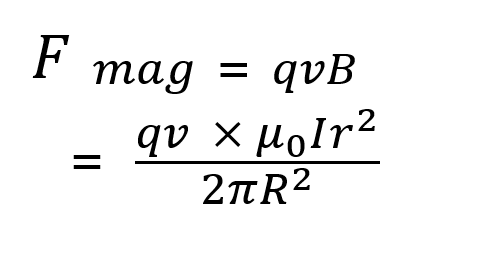Magnetic Field of a Long Thick Wire Using Ampere's Law

Claimed by Rahmel Bailey (Fall 2018)

The Main Idea

This page will explain and show how to use Ampere's Law to find the magnetic field of a long thick wire at a specified distance. It is much easier to calculate the magnetic field using Ampere's Law as opposed to Biot-Savart Law.

Analytical Model of Ampere's Law

Ampere's Law is a the relationship that exists between the pattern of the magnetic field along a path that is closed and the current that passing through that path.A path is any material that that a current can closed through that is connected and continuous, much like a wire loop.

For the Examples below, the path will be a circular loop. It is important to note that Ampere's law can only be used to calculate constant current.

 Ampere's Law Equation:

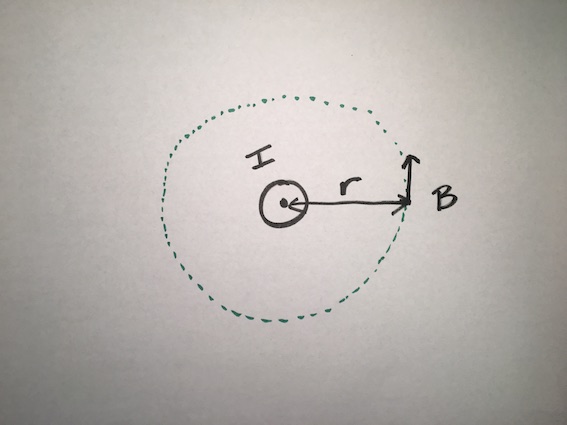
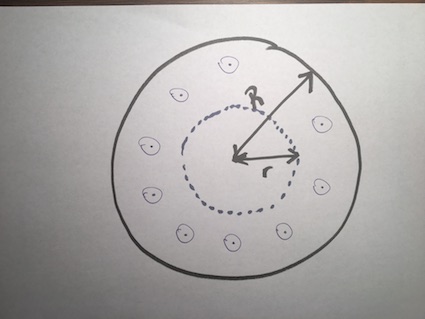
The following pictures display how to use Ampere's Law when trying to calculate the magnetic field of a current flowing out of the page at distance r away from the wire.

The diagram above shows a current-carrying wire with its current flowing out of the page. Using the right-hand rule, we can determine the direction of the magnetic field to be as shown. The dotted circle represents the Amperian loop of radius r.

The workings below, shows how Ampere's Law is used to calculate the magnetic field of the current-carrying wire at a distance r. Note that on the third line of working, the dot product disappears. This occurs because the direction of the magnetic field is the same as the direction of dl. More specifically, the angle between dl and the magnetic field B is 0. Remember the equation of the dot product is |a| x |b| x cos (theta). So in this case, a = B, b = dl and theta = 0. So if theta = 0 we know that cos (0) = 1. In the next line of working B is pulled out of the closed integral, this occurs because all along the Amperian loop the magnetic field is the same, it does not change in magnitude. In the next line of working, once we added up all the dl 's on the Amperian loop, that will give us the circumference of the Amperian loop. From there we make B the subject of the equation.

Explanation:

We will see how one can use Ampere's Law to calculate the magnetic field of a long thick wire in examples below.

Examples

Middling

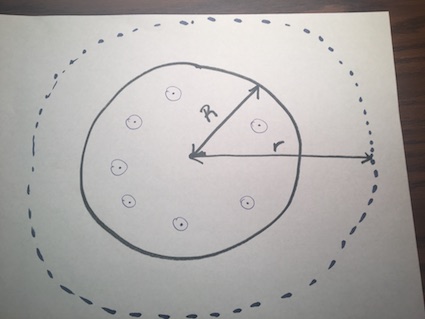
A long thick wire of radius R = 0.1 m has constant current I = 0.15 A flowing out of the page. An Amperian loop outside of the wire has radius r = 0.17 m. Calculate the magnetic field through the Amperian loop.

Explanation of the solution:

1) Write out Ampere's Law. The AL written as a subscript is short for Amperian Loop.

2) For the current, you can not calculate a ratio similar to the one calculated in the Simple question. Because the Amperian Loop is outside of the wire, the current you need is the current I flowing in the wire.

3) Remove the dot product on the right hand side of the equation because the direction of the magnetic field on the Amperian loop is the same as the direction of dl

4) Pull B out of the closed integral because it is the same all along the Amperian loop.

5) Complete the integral to give you the circumference of the Amperian loop. Keep in mind that the radius of the Amperian loop is not r (the radius of the wire), but it is R (the radius of the Amperian loop)

7) Substitute in the given values to give you 1.76e-7 T

Hard

A long thick wire has radius r = 0.1 m and a constant current of I = 0.15 A. The Amperian loop within the wire has radius r = 0.05 m. Calculate the magnetic force due to the Amperian loop, exerted on an electron moving at 4e7 m/s.

Explanation:

1) Refer to Simple question to calculate the magnetic field.

2) Once you've calculated the magnetic field, substitute this value into the equation for magnetic force.

3) Substitute in the given values to give you 4.8e-20 N.

Connectedness

Ampere's Law is particularly interesting because of how it is used as an alternative to the Biot-Savart Law. When studying this, I realized how that the relationships and laws in physics can be used to explain a multitude of things no matter how specific they may seem. Calculating the magnetic field of a long wire is connected to Mechanical Engineering because mechanical engineers need to know what the interacting forces are doing within a motor for example. Using parts of Ampere's Law, the magnetic field of wires within motors can be calculated. Magnetic fields and calculating their magnitudes is important in the motor industry, especially in the case of alternating current generators. For large-scale power alternating current generators, bigger magnetic fields are needed. These are produced from permanent magnets or coils of long wires.

History

In 1826, it was Hans Christian Oersted (in Denmark) who had discovered the connection between magnetism and electricity when he found that the needle of a compass he was holding was deflected when he moved it close to a current carrying wire during one of his lectures. It was this discovery that prompted the French physicist, Andre-Marie Ampere, to start his own research. Ampere was conducting experiments to learn more about the magnetic fields created by currents. Ampere found that when he placed two wires next to each other with current running in the same direction, the wires were attracted to each other and when the current was running in opposite directions, the wires repelled each other! Experiments like this and more gave way to the creation of Ampere's Law that helps people calculate the strength of magnetic fields and currents in particular situations.

Magnetic Field of a Long Thick Wire Using Ampere's Law

Contents

The Main Idea

Analytical Model of Ampere's Law

Examples

Middling

Hard

Connectedness

History

See also

Further reading

External links

References

Navigation menu