Heisenberg Uncertainty Principle

Claimed by Nicholas Maldonado 11/27/22

Heisenberg Uncertainty Principle

The Heisenberg uncertainty principle is a concept that describes uncertainty relationships between a particle's different properties, those being position and momentum, as well as energy and time.The biggest takeaway from this concept is that there is always some measure of uncertainty in at least one of any given particle's properties.

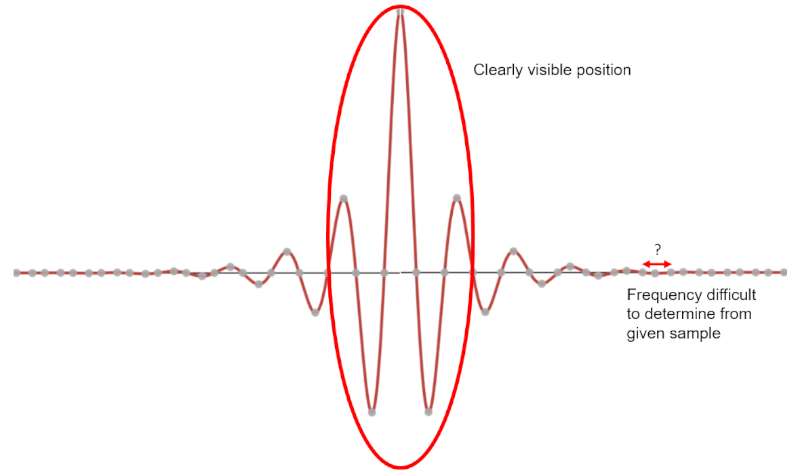
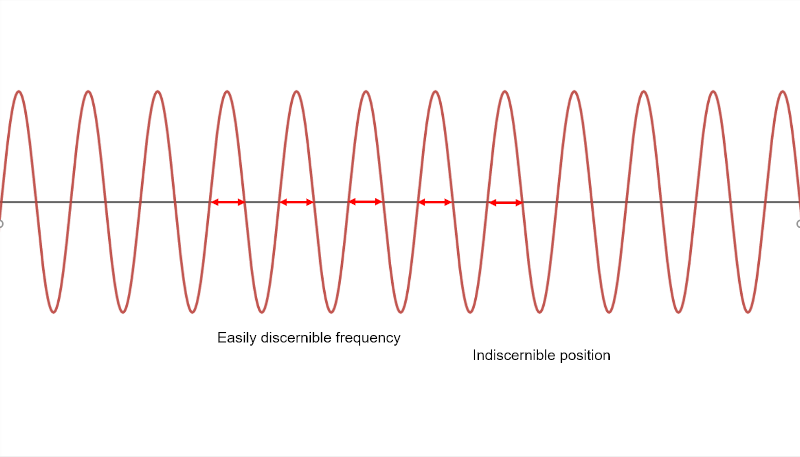
Generally speaking, uncertainty relationships are not unique to modern physics. This is a concept that occurs in classical physics as well. Consider a wave, described by some combination of sines and cosines. Any wave has an amount of uncertainty between its frequency and its position. For example, a wave with a single period would give you a lot of information about its position, but not much information about its frequency. Conversely, a wave of many periods would allow you to precisely determine its frequency, but the position of the wave would be less certain.

However, why would a particle obey this principle that appears to apply only to waves? Notice that objects at the quantum scale actually exhibit Wave-Particle Duality. Anything with a mass, including objects classically thought as discrete particles, have an associated wavelength. What this wave is exactly relates to the particle's position, which is innately probabilistic. The Uncertainty Principle naturally follows the result that this wavelength is dependent on a particle's momentum.

A Mathematical Model

An adequately rigorous derivation of the Heisenberg Uncertainty Principle requires knowledge in the mathematics governing quantum mechanical systems, namely linear algebra with abstract vector spaces. A high-level overview of the mathematics is instead given:

A quantum system, which in this case can be a single particle, is represented by a "state vector". The components of this vector contain information on the probabilities associated with measurements. Each "dimension" of this vector corresponds to a possible outcome, and the magnitudes of the vector along each dimension indicates the likelihood the particle will be found in the corresponding state.

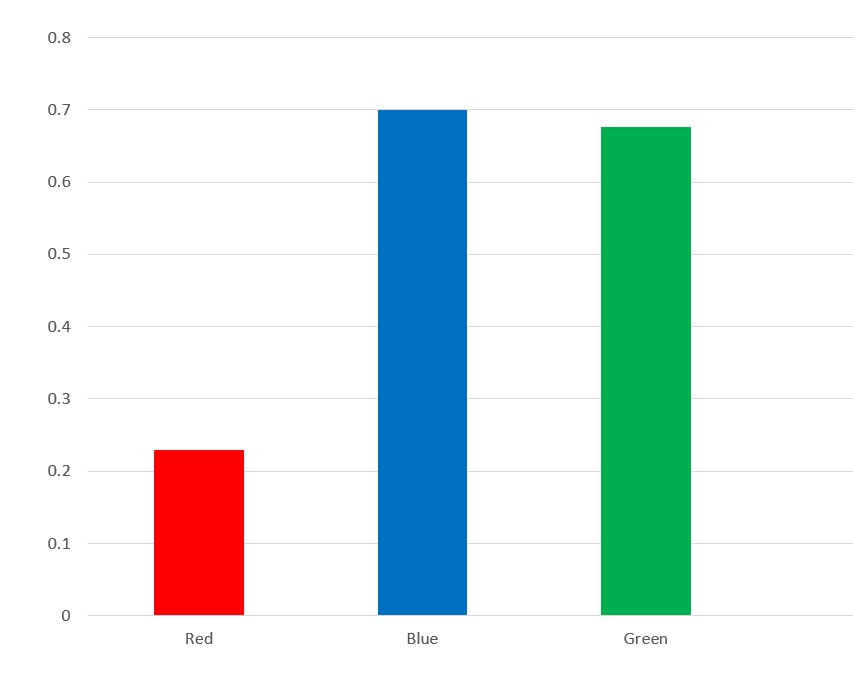
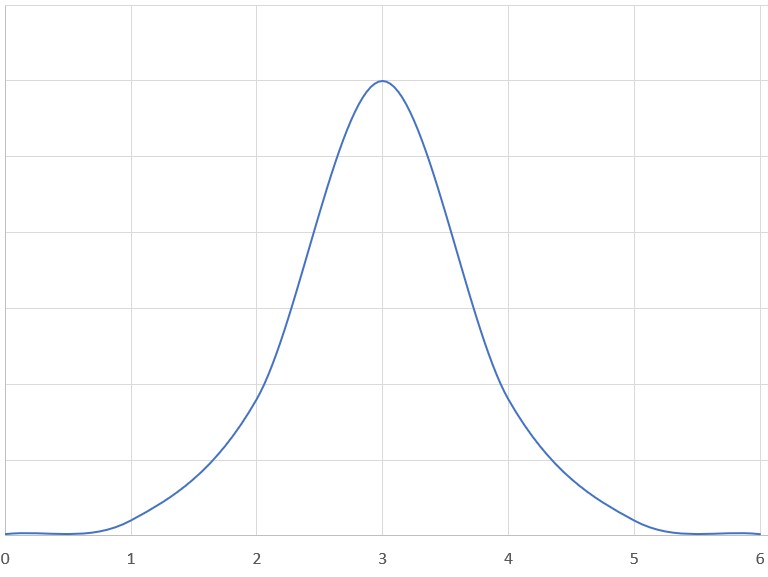
Above is a graph depicting the components of a quantum state vector. Each component corresponds to an outcome of a measurement, which in this case is the fictitious property "color". It is evident that it is more likely the particle will be found to be "blue" rather than "red" or "green". Below is a graph depicting the components of a state vector for a continuous property, like position. Every point on the curve corresponds to a component of the vector (it has an infinite number of dimensions). For example, the value at the x-value 3.32 gives us information on the likelihood the particle will be found around x=3.32.

An actual quantum state vector actually takes complex values for its components. It would be more accurate to add another dimension to both of the above graphs, indicating the imaginary part of each component. This has been omitted for simplicity. See The Born Rule for a more rigorous treatment of quantum state vectors.

The measurement of some property amounts to acting on this vector with an "operator". Every measurable quantity, like position, momentum, energy, and even angular momentum can be paired with a corresponding operator. What is important is the fact operators can alter the components of the vector, and thus the particle itself. It is not physically possible to measure two entirely distinct quantities at once, so measuring position and momentum means applying one operator and then another (or vice versa). It is then easy to see that the order of application matters. The way two operators can alter (or preserve) a particle's state is summarized by a mathematical object called the commutator. For two objects [math]\displaystyle{ {\hat{A}} }[/math] and [math]\displaystyle{ {\hat{B}} }[/math], the commutator is given by

[math]\displaystyle{ {\hat{A}\hat{B}-\hat{B}\hat{A}} }[/math].

Notice that this is not zero, as the order of the operators matter! From this the minimum uncertainty introduced in one property by the measurement of another property can be found.

The total uncertainty between a particle's position and momentum is given as [math]\displaystyle{ {\Delta p \Delta x} }[/math]. The minimum uncertainty a particle can have is [math]\displaystyle{ {\frac{{\hbar}}{2}} }[/math]. Therefore, we can establish the relationship of:

[math]\displaystyle{ {\Delta p \Delta x \geq \frac{{\hbar}}{2}} }[/math]

Oftentimes, it is also good enough to simply approximate their general relationship as:

[math]\displaystyle{ {\Delta p \Delta x} }[/math] ~ [math]\displaystyle{ {\hbar} }[/math]

NOTE: [math]\displaystyle{ {\hbar = \frac{{h}}{2\pi}} }[/math] where [math]\displaystyle{ {h} }[/math] is Planck's constant.

This principle can also be extended to a relationship between energy and time, where:

[math]\displaystyle{ {\Delta E \Delta t \geq \frac{{\hbar}}{2}} }[/math]

and

[math]\displaystyle{ {\Delta E \Delta t} }[/math] ~ [math]\displaystyle{ {\hbar} }[/math]

A Computational Model

TODO: ADD COMPUTATIONAL MODEL

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Examples

Simple

A particle is confined to a box 0.1 nm wide. Estimate the minimum uncertainty of its momentum.

Solution: The minimum uncertainties are related by [math]\displaystyle{ {\Delta x \Delta p \geq \hbar/2} }[/math]. Taking the uncertainty of the particle's position to be the width of the box, the uncertainty of the momentum is then

[math]\displaystyle{ {\Delta p \geq \frac{\hbar}{2\Delta x}\approx 5.27\times 10^{-25}} }[/math] kg m/s.

Middling

A muon ([math]\displaystyle{ {1.883531609\times 10^{-28}} }[/math] kg) from space was detected traveling 0.2c. What is the uncertainty of its position at the time of measurement, assuming momentum can be known to a certainty of [math]\displaystyle{ {\pm 10\%} }[/math] of its value?

Solution: The position uncertainty is related to its momentum uncertainty, which in turn is related to the particle's velocity. As the muon is traveling a significant fraction of the speed of light, the relativistic expression for momentum must be used,

[math]\displaystyle{ {p=mv\gamma} }[/math],

where [math]\displaystyle{ {\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}} }[/math] (see Lorentz Transformations). So the muon's momentum is [math]\displaystyle{ {1.15\times 10^{-20}} }[/math] kg m/s. Taking [math]\displaystyle{ {10\% p=\Delta p=1.15\times 10^{-21}} }[/math] kg m/s, the minimum uncertainty in position is

[math]\displaystyle{ {\Delta x \geq \frac{\hbar}{2\Delta p}=4.585 \times 10^{-14}} }[/math] meters.

Difficult

An emitted photon's wavelength has been determined to be 530 nm within a range of 2 nm. What is the uncertainty of the time of emission?

Solution: A photon's wavelength is related to its energy by [math]\displaystyle{ {E=c/\lambda} }[/math]. Uncertainty in energy and time are related by the Uncertainty principle, [math]\displaystyle{ {\Delta E \Delta t \geq \frac{\hbar}{2}} }[/math]. Uncertainties are relatively small quantities, making them analogous to differentials. So another relationship between wavelength and energy can be found:

[math]\displaystyle{ {dE=-hc/\lambda^2} }[/math], [math]\displaystyle{ {\Delta E =\frac{hc}{\lambda^2}\Delta \lambda} }[/math].

Now, equating the uncertainties in energy:

[math]\displaystyle{ {\frac{hc}{\lambda^2}\Delta \lambda \Delta t \geq \hbar/2 } }[/math], [math]\displaystyle{ {\Delta t\geq \frac{\hbar\lambda^2}{2\Delta \lambda hc}=3.728\times 10^{-14}} }[/math] seconds.

Connectedness

The Heisenberg uncertainty principle later plays into quantum tunneling, where this inherent uncertainty in a particle may sometimes allow it to overcome a potential energy barrier it otherwise would not be able to overcome classically (see Quantum Tunneling through Potential Barriers).
As a consequence of Heisenberg uncertainty principle, microelectronics are limited in size because electrons are able to tunnel through transistors that are small enough for uncertainty principle to have an effect.
Hydrogen nuclei are positively charged, so bringing two of them close enough together to fuse requires passing an Electric Potential. This takes a large amount of kinetic energy, corresponding to a temperature much higher than the cores of most stars. Tunneling allows particles with much lower kinetic energies to fuse. In other words, without tunneling, stars including our sun would produce no energy at all!

History

Quantum theory was first developed in the mid 1920s, with an emphasis on the observable properties of quantum systems. Heisenberg was guided by experimental results suggesting that the product of certain uncertainties around [math]\displaystyle{ {\hbar} }[/math]. He linked this to the mathematical formalism of linear operators. Namely, he and his contemporaries found the commutator of certain operators to be [math]\displaystyle{ {i\hbar} }[/math]. He reasoned that since simple measurements of wavelength, time, and position can only be done through interaction, the magnitude of such interactions must affect future measurements. For example, observing an electron amounts to sending or receiving a photon from it. However, doing this alters the electron.

Single-slit Diffraction Experiments

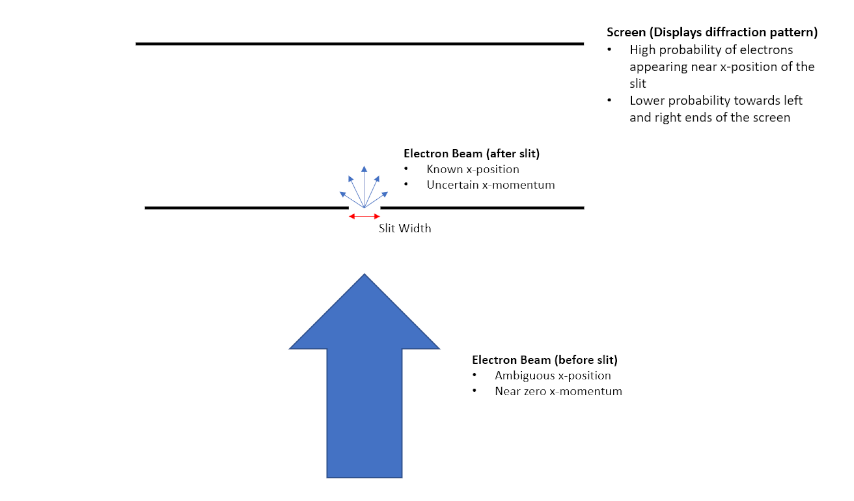
Heisenberg uncertainty relationships were first physically demonstrated through single-slit diffraction experiments. The experiment is conducted by launching beam of electrons through a narrow slit. Initially, the electrons have zero momentum in the x-direction. After passing through the slit, information about an electron's x position is acquired, resulting in an increased uncertainty in the particle's x momentum. Making the slit narrower therefore increases the uncertainty of the particle's x momentum while decreasing the uncertainty of its x position, while making the slit wider has the opposite effect. This effectively demonstrates the relationship between the uncertainty of a particle's position and momentum.

The Uncertainty Principle. Uncertainty principle. (n.d.). Retrieved April 20, 2022, from hyperphysics.phy-astr.gsu.edu

Libretexts. (2021, April 23). Heisenberg's Uncertainty Principle. Chemistry LibreTexts. Retrieved April 20, 2022, from chem.libretexts.org

Hilgevoord, Jan and Jos Uffink, "The Uncertainty Principle", The Stanford Encyclopedia of Philosophy (Winter 2016 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/win2016/entries/qt-uncertainty/>.

Heisenberg Uncertainty Principle

Contents