Head-on Collision of Equal Masses

Work in progress by mtikhonovsky3

Main Idea

A collision is a brief interaction between large forces. A head-on collision could be between two carts rolling or sliding on a track with low friction, billiard balls, hockey pucks, or vehicles hitting each other head-on.

In terms of the two carts of equal masses example, the two carts are the system. The Momentum Principle tells us that after the collision the total final momentum [math]\displaystyle{ p_{1xf} + p_{2xf} }[/math] must equal the initial total momentum [math]\displaystyle{ p_{1xi} }[/math]. Before the collision, nonzero energy terms included the kinetic energy of cart 1, [math]\displaystyle{ K_{1i} }[/math], and the internal energies of both carts. After the collision there is an increase in the internal energy of both carts and kinetic energy of both carts, [math]\displaystyle{ K_{1f} + K_{2f} }[/math].

A Mathematical Model

Head-on Collisions of Equal Masses can be based off the Fundamental Principle of Momentum:

[math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net}{Δt} }[/math]

where p is the momentum of the system, F is the net force from the surroundings, Δt is the change in time for the process. Energy Principle:

[math]\displaystyle{ {E}={Q}+{W} }[/math] where E is the total energy, Q is the heat given off, and W is the work done.

Based off of the Momentum Principle and the Energy Principle, we will explore Head-on Collisions of Equal Masses in two different scenarios: elastic and maximally inelastic (objects become stuck together).

1. Elastic Head-on Collisions of Equal Masses

Momentum Principle:

[math]\displaystyle{ {p_{xf}}={p_{xi}}+{F_{net,x}}{Δt} }[/math]

[math]\displaystyle{ {p_{1xf}}+{p_{2xf}}={p_{1xi}}+{0} }[/math]

Energy Principle:

[math]\displaystyle{ {E_f}={E_i}+{W}+{Q} }[/math]

[math]\displaystyle{ ({K_{1f}}+{E_{int1f}})+({K_{1f}}+{E_{int2f}})=({K_{1i}}+{E_{int1i}})+({K_{2i}}+{E_{int2i}})+{0}+{0} }[/math]

[math]\displaystyle{ {K_{1f}}+{K_{2f}}={K_{1i}}+{0} }[/math]

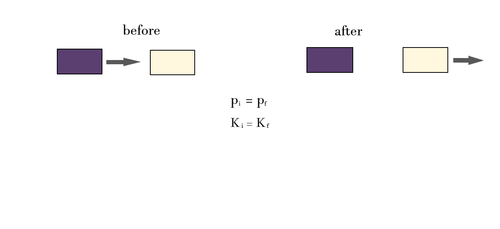
Since K=p²/2m, we can combine the momentum and energy equations:

[math]\displaystyle{ {\frac{p^{2}_{1xf}}{2m}}+{\frac{p^{2}_{2xf}}{2m}}= {\frac{(p_{1xf}+{p}_{2xf})^2}{2m}} }[/math]

[math]\displaystyle{ {p^2_{1xf}}+{p^2_{2xf}}={p^2_{1xf}}+{2p_{1xf}p_{2xf}}+{p^2_{2xf}} }[/math]

[math]\displaystyle{ {2p_{1xf}p_{2xf}}={0} }[/math]

There are two possible solutions: p_1xf =0 or p_2xf =0. If p_1xf =0, then object 1 came to a full stop. Based on the momentum equation p_1xf + p_2xf = p_2xf = p_1xi, then object 2 now has the same momentum that object 1 used to have. There is a complete transfer of momentum from object 1 to object 2, and so there is also a complete transfer of kinetic energy from object 1 to object 2. If p_2xf =0, then p_1xf + p_2xf = p_1xf = p_1xi, and so object 1 keeps going, missing object 2. This won't happen if the carts are on the same track. It is not possible for both final momenta to be zero, since the total final momentum of the system must equal the nonzero total initial momentum of the system.

2. Maximally Inelastic Collision of Equal Masses

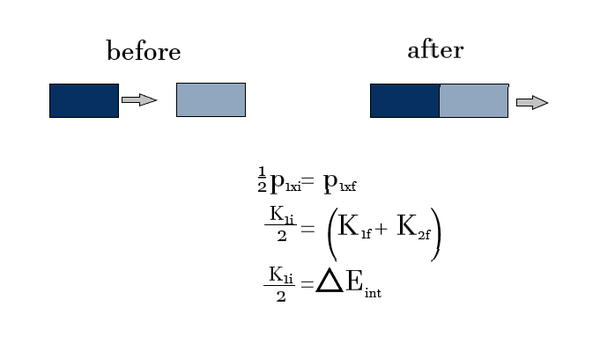
Momentum Principle:

[math]\displaystyle{ {p_{1xf}}+{p_{2xf}}={p_{1xi}} }[/math]

[math]\displaystyle{ {2p_{1xf}}={p_{1xi}} }[/math]

[math]\displaystyle{ {p_{1xf}}={\frac{1}{2}}{p_{1xi}} }[/math]

The final speed of the stuck-together carts is half the initial speed:

[math]\displaystyle{ {v_{f}}={\frac{1}{2}}{v_{i}} }[/math]

Final translational kinetic energy:

[math]\displaystyle{ ({K_{1f}}+{K_{2f}})={2}({\frac{1}{2}}{m}{v^2_{f}}) }[/math]

[math]\displaystyle{ ({K_{1f}}+{K_{2f}})={2}({\frac{1}{2}}{m}({\frac{1}{2}}{v_{i}})^2)={\frac{1}{4}}{m}{v^2_{i}} }[/math]

[math]\displaystyle{ ({K_{1f}}+{K_{2f}})={\frac{K_{1i}}{2}} }[/math]

Energy Principle:

[math]\displaystyle{ {K_{1f}}+{K_{2f}}+{E_{int,f}}={K_{1i}}+{E_{int,i}} }[/math]

[math]\displaystyle{ {E_{int,f}}-{E_{int,i}}={K_{1i}}-({K_{1f}}+{K_{2f}}) }[/math]

[math]\displaystyle{ {ΔE_{int}}={K_{1i}}-{\frac{K_{1i}}{2}} }[/math]

[math]\displaystyle{ {ΔE_{int}}={\frac{K_{1i}}{2}} }[/math]

The Momentum Principle is still valid even though the collision is inelastic, and fundamental principles apply in all situations. The final kinetic energy of the system is only half of the original kinetic energy, which mean that the other half of the original kinetic energy has been dissipated into increased internal energy of the two carts.

From both examples, we know:

1. If the collision is elastic, object 1 stops and object 2 moves with the speed object 1 used to have.

2. If the collision is maximally inelastic, the carts stick together and move with half the original speed. Half of the original kinetic energy is dissipated into increased internal energy.

A Computational Model

This simulation shows the head on collision of two balls of equal mass.

Examples

Simple

Question

A 8 kg mass traveling at speed 18 m/s strikes a stationary 8 kg mass head-on, and the two masses stick together. What are the final speeds?

Answer

[math]\displaystyle{ {m}{v_{1i}}+{m}{v_{2i}}={m}{v_{f}}+{m}{v_{f}} }[/math]

[math]\displaystyle{ {m}{v_{1i}}+{m}({0})={2m}{v_{f}} }[/math]

[math]\displaystyle{ {8 kg}({18m/s})={2}({8kg}){v_{f}} }[/math]

[math]\displaystyle{ {144kg}{m/s}={16 kg}{v_{f}} }[/math]

[math]\displaystyle{ {v_{f}}={9m/s} }[/math]

Middling

Question

Toyota is testing the crash-safety of their new car. They crash two cars in a head on collision, one moving 30 miles per hour and one moving 45 miles per hour. The cars are they same model, so they both weigh 3,500 pounds. Assuming the cars stick together, what is their speed immediately after the collision?

Answer

This is a Maximally Inelastic Collision since the cars stick together. Therefore, we can use conservation of momentum to calculate the final speed.

First, it is useful to convert all given measurements into the metric system. This isn't a totally necessary step, but I find it makes the problem easier and saves time in the end. It is necessary, however, to convert the given weight measurement to a mass measurement.

[math]\displaystyle{ {30 mph} * \frac{1609.34 meters}{1 mile} * \frac{1 hour}{3600 seconds} = 13.41 m/s }[/math]

[math]\displaystyle{ {45 mph} * \frac{1609.34 meters}{1 mile} * \frac{1 hour}{3600 seconds} = 20.12 m/s }[/math]

[math]\displaystyle{ {3500 pounds} * \frac{4.448 newtons}{1 pound} = 15568.78 N }[/math]

[math]\displaystyle{ {15568.78 newtons} * \frac{1}{9.81 m/s} = 1,587 kg }[/math]

[math]\displaystyle{ {m}{v_{1i}}+{m}{v_{2i}}={m}{v_{f}} }[/math]

[math]\displaystyle{ (1587)(13.41)+(1587)(20.12)=(3174)(v_{f}) }[/math]

[math]\displaystyle{ {21281.67}+{31930.44}={3174}{v_{f}} }[/math]

[math]\displaystyle{ {53212.11}={3174}{v_{f}} }[/math]

[math]\displaystyle{ {v_{f}}={16.77m/s} }[/math]

The cars move at a speed of 16.77 meters per second immediately after the crash. Note that this does not take into account the energy lost in the form of heat or deformation of the car.

Difficult

Question

You're playing pool and hit the 1 ball with the cue ball at a velocity of 4 meters per second. The 1 ball then bounces off the side of the table and unfortunately then knocks the 8 ball in a pocket. The 8 ball takes 2.5 seconds to roll into the pocket. How far away was the 8 ball from the pocket? Assume that all the balls have a mass of .17 kg and that friction is negligible.

Answer

This question requires a lot of information to keep straight. Let's work backwards from the final question to find the information we need.

We can use the kinematic equation [math]\displaystyle{ d = \frac{v_0+v_f}{2}t }[/math] to find the distance to the pocket. We have [math]\displaystyle{ t = 2.5 }[/math] and [math]\displaystyle{ v_f = v_0 }[/math] since friction is negligible. Now we have to find [math]\displaystyle{ v_0 }[/math] by starting with the first collision.

Since this is a head-on collision of equal mass, we can say that all of the cue ball's momentum was transferred to the 1 ball such that it continues with a velocity of 4 meters per second.

We can use [math]\displaystyle{ m_{1,0}v_{1,0} + m_{table,0}v_{table,0} = m_{1,f}v_{1,f} + m_{table,f}v_{table,f} }[/math] to find the velocity of the ball after the collision.

[math]\displaystyle{ (.17)(4) + m_{table,0}(0) = (.17)v_{1,f} + m_{table,f}(0) }[/math]

[math]\displaystyle{ v_{1,f} = 4 }[/math]

Since friction is negligible, we can say that the 1 ball also hits the 8 ball with a velocity of 4 meters per second. Here, we can say the same thing we said about the collision between the cue ball and the 1 ball. Since it is a head-on collision of equal mass, the velocity of the 8 ball must be 4 meters per second.

Now, we can finally return to the kinematics equation [math]\displaystyle{ d = \frac{v_0+v_f}{2}t }[/math].

[math]\displaystyle{ d = \frac{4+4}{2}(2.5) = 1.6 meters }[/math]

The 8 ball was 1.6 meters away from the pocket, a real skill shot.

Connectedness

A real world application of head-on collisions of equal mass are billiard balls (playing pool). All the balls have equal mass, and one ball is shot towards another, which is stationary. When the two collide, the ball that is hit will move at a 180 degree angle from the direction the striking ball comes from. Keeping this mind and with a little practice one's level of playing billiards should increase.

Another fun application of collisions of equal mass is bumper cars. While the tracks are not typically low enough friction to discount it, the cars approximately all have the same mass and collide frequently. Changes in momentum with collisions are easy to exemplify with bumper cars. For example, it is easy to observe how two bumper cars going the same speed collide and bounce backwards; while one fast car hitting a stationary one causes a larger transfer of energy.

History

The idea of inelastic collisions is rooted in the conservation of linear momentum, which is implied by Newton's Laws. Newton published his book, the Philosophiae Naturalis Principia Mathematica, in 1687. This book, commonly known as Principia, described Newton’s findings on collisions and laid a foundation for the different types of collisions we study today.

The history of collisions in modern physics starts with Rutherford’s Gold Foil experiment. He found that while they did not touch, the alpha particles and the gold nucleus collided elastically. It is essential that the collision was elastic, in that it gives us the famous scatting pattern and led to the discovery of the positively charged nucleus.

Head-on Collision of Equal Masses

Contents

Main Idea

A Mathematical Model

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu