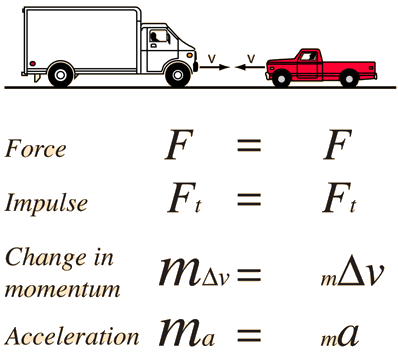
Head-on Collision of Unequal Masses
claimed by gdweck3
Main Idea
A collision is any incident in which there is little interaction before and after a short time interval, during which there is a large interaction. The two main types of collisions are Elastic Collisions and Inelastic Collisions, but these are very broad as there are many much more specific types of collisions under these umbrella terms. One specific type of collisions is head-on collisions of unequal masses. This is exactly what it sounds like - two objects of different masses collide with each other head-on, causing changes in kinetic energy and momentum. To make this easier to visualize, imagine a ping-pong ball colliding with a bowling ball. You would observe the ping-pong ball bounce straight back with very little change in speed, and much less obviously, you will see the bowling ball's speed will also be altered.
It is generally true that when a low-mass projectile collides elastically with a stationary large mass, the low-mass projectile will bounce off with little change in speed or kinetic energy, but a large change in momentum. The large mass, on the other hand, will gain lots of momentum with very little change in speed or kinetic energy.
A Mathematical Model
Most commonly, head-on collisions of unequal masses are studied as elastic collisions, in which case, kinetic energy is conserved. What this means is that the total final kinetic energy of the system is equal to the total initial kinetic energy of the system. In equations, it looks like this: [math]\displaystyle{ {1 \over 2}m_1v_{1i}^2 + {1 \over 2}m_2v_{2i}^2 = {1 \over 2}m_1v_{1f}^2+ {1 \over 2}m_2v_{2f}^2 }[/math].
As you can see the from the equations above, the momentum principle can be applied to derive each of the equations yielding solutions for final momentum and velocity of both objects.
If the equation is inelastic, the idea of conservation of momentum can be used because momentum is always conserved in collisions. The equation for the conservation of momentum is: [math]\displaystyle{ m_1v_{1,i}^2 + m_2v_{2,i}^2 = m_1v_{1,f}^2 + m_2v_{2,f}^2 }[/math]
As referenced to before, the ping-pong and bowling ball example clearly demonstrates what occurs in a head on collision of unequal masses. Say the system consisting of the ping-pong and bowling balls is in outer space. The ping-pong ball of mass m is traveling in the +x direction with initial momentum [math]\displaystyle{ p_{1,i} }[/math], and hits a stationary bowling ball of mass M head on.
Since the bowling ball is at rest when the ping pong ball hits it, the final momentum of the bowling ball is twice the initial momentum of the ping pong ball. This can be seen by using the conservation of momentum principle: [math]\displaystyle{ m_1v_{1,i}^2 + m_2v_{2,i}^2 = m_1v_{1,f}^2 + m_2v_{2,f}^2 }[/math] where p=mv.
Assume the speed of the ping-pong ball doesn't change significantly, so if [math]\displaystyle{ p_{1f} ≈ -p_{1i} }[/math], then: [math]\displaystyle{ -p_{1,i} + p_{2,f} = p_{1,i} }[/math] and [math]\displaystyle{ p_{2,f} = 2p_{1,i} }[/math]
Knowing the speed of the ping pong ball remains about the same, the new equation is [math]\displaystyle{ -p_{1,i} + p_{2,f} = p_{1,i} }[/math] which gives [math]\displaystyle{ p_{2,f} = 2p_{1,i} }[/math] showing that the final momentum of the bowling ball is twice the initial momentum of the ping pong ball. Although this is a very specific circumstance, different variables of the equation can be solved for by using the conservation of momentum principle.
In summary, when the ping-pong ball hits the stationary bowling ball, head-on and elastically:
- The ping-pong ball bounces back with nearly the same speed, but has a large change in momentum [math]\displaystyle{ -2p_{1i} }[/math].
- The bowling ball also has a large change of momentum [math]\displaystyle{ +2p_{1i} }[/math], even though its final speed is very small due to a large mass.
- The bowling ball's final kinetic energy is very small due to a low speed.
This is just an example of applying the conservation of momentum principle and being able to make many deductions. This example proves the introductory claim that generally when low mass projectiles collide elastically with stationary large masses, the low-mass projectile will bounce off with little change in speed.
A Computational Model
Glowscript model of a head-on collision of unequal masses
Examples
Simple
Question
You just got a 100 on your last physics test and are so psyched you throw your .15 kilogram calculator down on your bed. It hits your bed at a velocity of 6 meters per second and bounces off at a velocity of 1.5 meters per second. How much momentum and kinetic energy did your calculator lose from the collision?
Answer
Momentum [math]\displaystyle{ = m_{calc,i}v_{calc,i} }[/math] before the collision and momentum [math]\displaystyle{ = m_{calc,f}v_{calc,f} }[/math] after the collision.
Therefore, change in momentum [math]\displaystyle{ = |m_{calc,f}v_{calc,f} - m_{calc,i}v_{calc,i}| }[/math].
Substituting the given information in, we get [math]\displaystyle{ = |(.15)(1.5) - (.15)(6)| = 0.675 kgm/s }[/math].
We can use a similar method to solve for the change in kinetic energy using the formula [math]\displaystyle{ K = \frac{1}{2}mv^2 }[/math], so that change in kinetic energy is [math]\displaystyle{ = |\frac{1}{2}m_{calc}v_{calc,f}^2 - \frac{1}{2}m_{calc}v_{calc,i}^2| }[/math].
Substituting the given information in again, we get [math]\displaystyle{ = |\frac{1}{2}(.15)(1.5^2) - \frac{1}{2}(.15)(6^2)| = 2.53 J }[/math]
Middling
Difficult
Question
In an orbiting spacecraft a ping-pong ball of mass m (object 1) traveling in the +x direction with initial momentum [math]\displaystyle{ p_{1i} }[/math] hits a stationary bowling ball of mass M (object 2) head on. What are the a) momentum, b) speed, and c) kinetic energy of each object after the collision? Assume little change in the speed of the ping-pong ball, and assume that the collision is elastic.
Answer
1. [math]\displaystyle{ -p_{1,i} + p_{2,f} = p_{1,i} }[/math] [math]\displaystyle{ p_{2,f} = 2p_{1,i} }[/math]
Because momentum is conserved, it can be seen that the final momentum of the bowling ball is twice the initial momentum of the ping-pong ball.
2. [math]\displaystyle{ V_{2,f} = {P_{2,f} \over M} = {2P_{1,i} \over M} = {2mv_{1,i} \over M} = 2{m \over M}V_{1,i} }[/math]
This will be a very small speed, considering m<<M.
3. [math]\displaystyle{ K_{2,f} = {(2p_{1,i})^2 \over 2M} }[/math] and [math]\displaystyle{ K_{1,f} = {(p_{1,i})^2 \over 2m} }[/math]
Because the mass of the bowling ball (M) is much larger than the mass of the ping-pong ball, the kinetic energy of the bowling ball is much smaller than the kinetic energy of the ping-pong ball.
Connectedness
Collisions in general have a multitude of applications in everyday life and in other fields. We encounter collisions almost all the time, especially collisions of unequal mass. It is more common outside of a lab setting to encounter collisions between objects of different masses. For example; a drumstick hitting a drum, a baseball hitting a bat, or a foot stepping on the ground.
Collisions of unequal masses are also vital in other branches of science and engineering. For example, in astronomy, these collisions are useful in studying asteroid interactions. If an asteroid is massive enough or has a great enough velocity, it can cause a noticeable change in momentum or energy in a more massive object. For example, one theory of the Moon's creation is that a very massive asteroid collided with a relatively young Earth and split into two large chunks, which were smoothed and condensed by gravity to become the Earth and the Moon.
In mechanical engineering, it is important to consider collisions of unequal mass to design for any intended or unintended impacts. Preparing for collisions with objects of different masses helps to create a safer and more durable product. This is also a consideration in marketing and for safety engineers.
History
The idea of inelastic collisions is rooted in the conservation of linear momentum, which is implied by Newton's Laws. Newton published his book, the Philosophiae Naturalis Principia Mathematica, in 1687. This book, commonly known as Principia, described Newton’s findings on collisions and laid a foundation for the different types of collisions we study today.
The history of collisions in modern physics starts with Rutherford’s Gold Foil experiment. He found that while they did not touch, the alpha particles and the gold nucleus collided elastically. It is essential that the collision was elastic, in that it gives us the famous scatting pattern and led to the discovery of the positively charged nucleus.
See also
Further reading
Matter and Interactions By Ruth W. Chabay, Bruce A. Sherwood - Chapter 10
External links
Tennis Ball and Bowling Ball Collision
Head-on Collision of Unequal Masses