Static Friction: Difference between revisions
| Line 53: | Line 53: | ||
===2. (Middling)=== | ===2. (Middling)=== | ||
A box of mass <math>m</math> sits on an inclined plane. The coefficient of static friction between the box and the inclined plane is <math>\mu_s</math>. What is the steepest the inclined plane can be without the box slipping down the ramp? | |||
[[File: | [[File:staticfrictionboxonramp.png]] | ||
Solution: | Solution: | ||
Let us call the angle that the box makes with the horizontal <math>\theta</math>. This makes the gravitational force down the ramp <math>mg\sin\theta</math> and the normal force between the box and the ramp <math>mg\cos\theta</math>. | |||
[[File: | [[File:staticfrictionboxonrampforcediagram.png]] | ||
When the ramp is as steep as it can be without slipping, the gravitational force down the ramp is balanced by the maximum possible static friction force up the ramp, so the following equation is true: | |||
<math>mg\sin\theta = F_{s, max}</math> | |||
<math>mg\sin\theta = \mu_s * N</math> | |||
<math>mg\sin\theta = \mu_s * mg\cos\theta</math> | |||
dividing both sides by <math>mg\cos\theta</math> yields | |||
<math>\tan\theta = \mu_s</math> | |||
<math>theta = \tan^-1\mu_s</math> | |||
===3. (Difficult)=== | ===3. (Difficult)=== | ||
Revision as of 13:38, 5 July 2019
This page defines and describes static friction. Some of the information presented on this page is also present on the Friction page.
The Main Idea
Static friction is a type of Friction between two touching objects that are not moving with respect to each other at their point of contact. When two objects touch each other and there is no sliding between their surfaces of contact, they exert static friction forces on each other. The static friction force acting on each object opposes any force that would cause it to slide relative to the other object. For example, consider a heavy dresser at rest on the floor. If a child pushes against the side of the dresser in an attempt to slide it, that exerts a force on the dresser, but the ground would exert on it an equal and opposite static friction force that balances the force exerted by the child, so the dresser stays at rest. The static friction force can take on whatever direction and magnitude necessary to balance an external net force that threatens to cause sliding motion between two surfaces. However, the magnitude of the static friction force is limited by a maximum value. If the external force becomes strong enough, the static friction force can be overcome and the surfaces can begin to slide, at which point the friction between the objects becomes Kinetic Friction. For example, now consider an adult pushing against the same heavy dresser. The adult can exert a stronger force than the child, and if it exceeds the maximum possible static friction force, the dresser can be set into motion and slid across the floor.
Rolling Friction
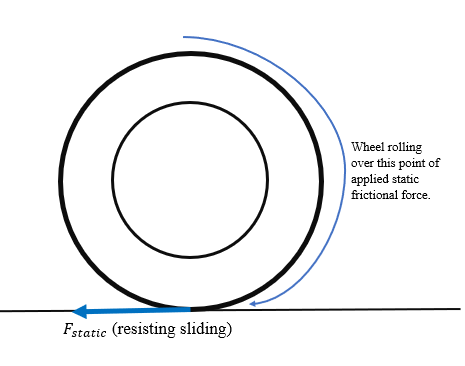
Friction is responsible for the rolling of round objects. When this rolling happens without slipping, the friction is static. Consider a wheel rolling without slipping across the ground. At a glance, it may seem like the friction between the wheel and the ground should be kinetic because the center of the wheel moves relative to the ground. However, to determine the type of friction acting between the wheel and the ground, one must look at the point of contact between them. The point of contact between the wheel and the ground occurs on the edge of the wheel on its lowest point, which is not moving relative to the ground. The point of contact between the wheel and the ground constantly changes but does not slide.
For an object rolling at a constant speed, the magnitude of the static friction force is 0 because there are no forces threatening to cause the wheel to slip. For an accelerating rolling object, however, such as a disk rolling down a ramp, the friction force has a nonzero magnitude to prevent the disk from slipping. Without this friction force, a disk placed on a ramp would simply slide down without rotating. It is important to ask oneself whether the static friction force acting on an accelerating rolling object is capable of doing work. The answer depends on whether the rolling object is modeled as a Point Particle System or a Real System. If the system is treated as a point particle, the static friction force is treated as though it acts on the particle's center of mass. It is therefore exerted over a distance and does work, affecting the object's total kinetic energy. If the system is treated as a real object, the static friction force is recognized as acting on the object's stationary edge, and therefore does no work. For the real system, the object's total kinetic energy would be the same even if the static friction force at its edge were absent. The only difference is that now some of its kinetic energy is rotational rather than translational. Point particles cannot have rotational kinetic energy, so the static friction force is treated as though it does work to account for the difference in total kinetic energy.
A Mathematical Model
As described above, the magnitude of the static friction force ([math]\displaystyle{ F_s }[/math]) between two objects is bounded by a maximum value. This maximum static friction force is given by
[math]\displaystyle{ F_{s, max} = \mu_s * N }[/math]
where [math]\displaystyle{ \mu_s }[/math] is the coefficient of static friction of the objects and [math]\displaystyle{ N }[/math] is the normal force between the objects. [math]\displaystyle{ \mu_s }[/math] is a property of the materials of the surfaces in contact and is usually less than 1. [math]\displaystyle{ \mu_s }[/math] has no units because it is a ratio of one force to another.
Often for problems involving rolling friction, the static friction never reaches its maximum allowed by the formula above. In fact, you may not be told the value the coefficient of static friction, only that it is high enough to prevent the object from slipping. For such problems, you may be asked to find some unknown quantity, such as the acceleration of a disk rolling down a ramp, which may seem difficult if the value of the friction force is unknown. To solve such a problem, a system of equations should be devised, where one equation relates the friction force to the translational acceleration of the disk and another equation relates the friction force to the rotational acceleration of the disk. For more information, see Rolling Motion.
A Computational Model
This is a VPython simulation of a box held in place by static friction. A steadily increasing external force, shown by the green arrow, is balanced by an equal and opposite static friction force, until the magnitude of the external force exceeds [math]\displaystyle{ \mu_s * N }[/math]. At this time, the box begins to move and the friction becomes kinetic.
Click "View this program" on the top left corner to view the VPython code.
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
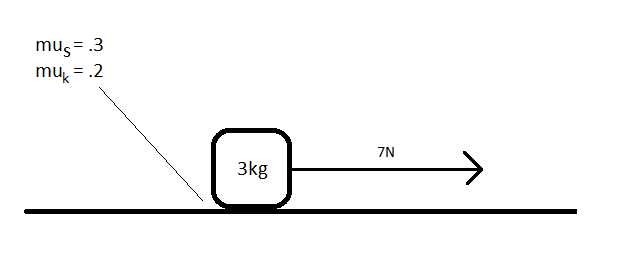
1. (Simple)
A box sits at rest on a table. The box has a mass of 3kg, the coefficient of static friction between the box and the table is .3, and the coefficient of kinetic friction between the table is .2. A horizontal external force of 7N is applied to the box. Does the box remain at rest?
Solution:
The maximum static friction force [math]\displaystyle{ F_{s, max} }[/math] is given by the equation
[math]\displaystyle{ F_{s, max} = \mu_s * N }[/math]
Since the table is a horizontal surface and the box is not accelerating vertically, the normal force must be equal in magnitude to the block's weight, or [math]\displaystyle{ 3 * 9.8 = 29.4 }[/math] N.
[math]\displaystyle{ F_{s, max} = .3 * 29.4 = 8.82 }[/math]N
The external force is only 7 N, and the static friction force can be up to 8.82N, so the static friction force is able to balance the external force and keep the block at rest.
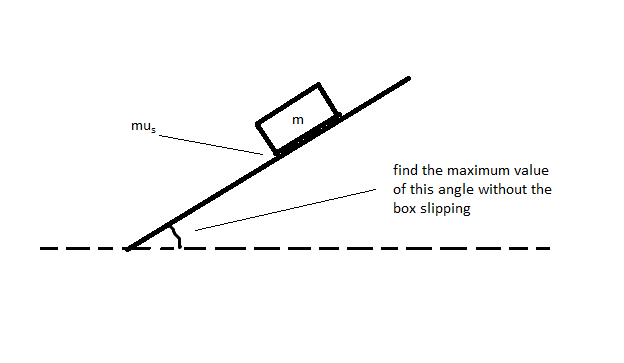
2. (Middling)
A box of mass [math]\displaystyle{ m }[/math] sits on an inclined plane. The coefficient of static friction between the box and the inclined plane is [math]\displaystyle{ \mu_s }[/math]. What is the steepest the inclined plane can be without the box slipping down the ramp?
Solution:
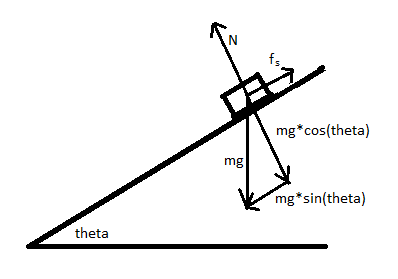
Let us call the angle that the box makes with the horizontal [math]\displaystyle{ \theta }[/math]. This makes the gravitational force down the ramp [math]\displaystyle{ mg\sin\theta }[/math] and the normal force between the box and the ramp [math]\displaystyle{ mg\cos\theta }[/math].
When the ramp is as steep as it can be without slipping, the gravitational force down the ramp is balanced by the maximum possible static friction force up the ramp, so the following equation is true:
[math]\displaystyle{ mg\sin\theta = F_{s, max} }[/math]
[math]\displaystyle{ mg\sin\theta = \mu_s * N }[/math]
[math]\displaystyle{ mg\sin\theta = \mu_s * mg\cos\theta }[/math]
dividing both sides by [math]\displaystyle{ mg\cos\theta }[/math] yields
[math]\displaystyle{ \tan\theta = \mu_s }[/math]
[math]\displaystyle{ theta = \tan^-1\mu_s }[/math]
3. (Difficult)
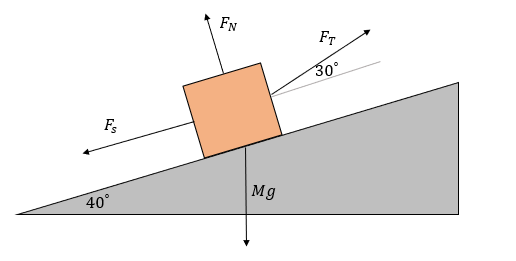
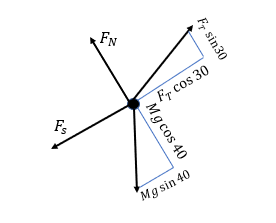
There is a crate of mass 20 kg sitting on a 40-degree inclined ramp that must be pulled to the top of the ramp to be loaded on a truck for delivery. A worker begins applying a force [math]\displaystyle{ {F}_{T} }[/math] to the crate by pulling on a rope attached to the crate at a 30-degree angle above the incline. If the coefficient of static friction [math]\displaystyle{ {μ}_{s} }[/math] is 0.27, what tension force must the worker apply to the crate in order to begin moving the crate up the ramp?
To begin solving this problem, we must draw a free body diagram in order to easily set up our force equations in order to solve for the tension force. We are going to set the x axis as the hypotenus of the incline and the y axis as the perpendicular to the incline hypotenuse. This should make it easier to break forces up into components. So, the FBD should look something like this:
Now, these forces can be further broken up into x and y components for two separate force equations:
With this new diagram, we can set up the equations for the forces in the x direction and the y direction. We can set both of these equations equal to zero because the crate still isn't moving, so acceleration is zero based on the equation [math]\displaystyle{ {F} = {M}{a} }[/math].
Forces in the x direction:
- [math]\displaystyle{ {F}_{T}{cos(30)} - {F}_{s} - {Mgsin(40)} = {0} }[/math]
Forces in the y direction:
- [math]\displaystyle{ {F}_{N} + {F}_{T}{sin(30)} - {Mgcos(40)} = {0} }[/math]
In order to solve for the applied tension force, we must get [math]\displaystyle{ {F}_{s} }[/math] in terms of known values. Therefore, we must use the coefficient of static friction to solve for this static frictional force in terms of mass, g, coefficient of friction, and the angles given. To do this, we can use the equation of the forces in the y direction to plug in a term for [math]\displaystyle{ {F}_{N} }[/math]:
- [math]\displaystyle{ {F}_{s} = {μ}_{s}({Mgcos(40)} - {F}_{T}{sin(30)}) }[/math]
This can then be plugged back into the equation for the forces in the x direction:
- [math]\displaystyle{ {F}_{T}{cos(30)} - {μ}_{s}({Mgcos(40)} - {F}_{T}{sin(30)}) - {Mgsin(40)} = {0} }[/math]
Then just isolate [math]\displaystyle{ {F}_{T} }[/math] in terms of the values given in the problem:
- [math]\displaystyle{ {F}_{T} = \frac{{μ}_{s}{Mgcos(40) + Mgsin(40)}}{cos(30) + {μ}_{s}{sin(30)}} }[/math]
Just plug in the values and solve for [math]\displaystyle{ {F}_{T} }[/math]:
- [math]\displaystyle{ {F}_{T} = \frac{(0.27)(20)(9.8)cos(40) + (20)(9.8)sin(40)}{cos(30) + (0.27)sin(30)} = {166.36 N} }[/math]
So, the crate must be pulled with a tension force of 166.36 N in order to overcome static friction and begin pulling the crate up the ramp to the truck.
Real Life Application
Static friction is a much more important Physics concept than most people think because this static friction plays such a big roll in so many different systems. For example, wheels are able to rotate solely due to static friction because it prevents the wheel from "slipping" with the surface that it makes contact with. The ground applies a static frictional force to the wheel at the point of contact so that the wheel will "roll" over that point without truly spinning.
Static friction can also be seen elsewhere such as walking and running which is achieved through the static friction between our shoe and the ground. The friction itself allows us to push forward using the static friction between our shoe and the ground as a pivot.
Overall, static friction is a relatively basic Physic's concept that plays a big role in our everyday life without us truly noticing. Try keeping your eyes open for different systems of motion and how static friction might play a role on the movement in that system.
Different types of friction
When getting into world application, friction in general can be seen in many different systems as discussed before. To be specific, some of the most common systems of friction are skin friction for contact between fluids and the skin, internal friction for deformation of bodies, belt friction for pulley systems with belts wrapping around them, fluid friction for viscosity, and even radiation friction for movement of matter.
It is sometimes difficult to recognize the presence of friction for complex concepts like fluids and motion of matter, but these are all forms of this static friction at a molecular level where atoms come in contact with each other and prevent one another from passing by or moving.
Regardless, friction almost always converts energy of a system to thermal energy. Since conservation of energy states energy cannot be created nor destroyed, friction can't just "destroy" energy when acting on an object, but instead causes the system to lose energy by converting energy to thermal energy which is then lost to the surroundings. This thermal energy loss can even be calculated by taking the integral of the frictional force over a distance in which the friction acts on an object:
- [math]\displaystyle{ {E}_{thermal} = \int{{F}_{static}{(x)dx}} }[/math]
And this can then be simplified to
- [math]\displaystyle{ {E}_{thermal} = \int{{F}_{normal}{μ}{(x)dx}} }[/math]
See also
Look below
Further reading
External links
- A couple of animations[3]
References
The book we used in class was a reference utilized in the creation of this page:
Matter and Interactions 4th edition. Full Citation: Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print.