Relative Velocity: Difference between revisions
| Line 45: | Line 45: | ||
Let us call east and north the +x and +y directions respectively. | Let us call east and north the +x and +y directions respectively. | ||
In this problem, there are two frames of reference: the water and the riverbank. Using trigonometry, we can find the velocity of the rowboat relative to the water: <math>\left \langle {-1.5\sin\theta,1.5\cos\theta} \right \rangle</math> | In this problem, there are two frames of reference: the water and the riverbank. Using trigonometry, we can find the velocity of the rowboat relative to the water: <math>\left \langle {-1.5\sin\theta,1.5\cos\theta} \right \rangle</math>. | ||
Now, by the formula | |||
== See also == | == See also == | ||
Revision as of 15:48, 9 August 2019
This page defines and describes relative velocity.
The Main Idea
Velocity is a relative property, meaning that its value depends on the frame of reference from which it is observed and has no absolute "true" or "correct" value. This is because the position and therefore velocity of an object can only be defined relative to some coordinate system determined by the frame of reference chosen to model the situation. If two frames of reference are not moving with respect to each other, they will observe the same velocity for a given particle (even if their origins lie in different places), but if two frames of reference are moving with respect to each other, they will observe different velocity values for the same particle.
Consider a car driving down the highway. Suppose you want to determine the velocity of its driver. To do this, you must choose a frame of reference. You might choose the road, in which case the driver might have a velocity of 60mph in the northerly direction. However, you might also choose the car itself, in which case the driver would be at rest. The driver's position within the car does not change over time, so the velocity of the driver relative to the car is 0. You might even choose the center of the earth as a frame of reference, in which case the velocity of the driver would be more than 1000mph in the easterly direction due to the rotation of the earth (plus 60mph in the northerly direction because of the car's movement along the highway). The universe does not have a "natural" or "true" reference frame, so no choice of reference frame or observed velocity is more objectively correct than any other. That said, depending on why you want to know the driver's velocity, one choice of reference frame might be more useful to you than others for your specific situation. For example, if you are trying to determine how much danger the driver would be in in the event of a collision with a tree, you would want to know their velocity relative to that tree (which would be the same as their velocity relative to the road because the tree and the road are not moving with respect to each other). However, if you are trying to determine how much danger the driver would be in in the event of a collision with another car, you would want to know their velocity relative to that other car, which might be very low if the other car is traveling in the same direction or very high if the other car is traveling in the opposite direction.
A Mathematical Model
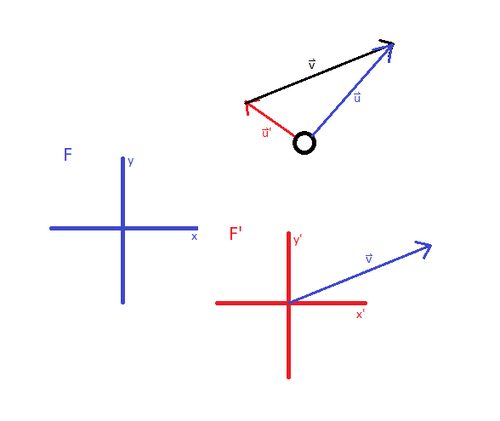
Observers in different reference frames may observe different velocities for the same particle, but that doesn't mean the two observations are unrelated to each other or cannot be compared. An equation exists that describes the relationship between velocities measured in different frames. That way, a velocity measured in one frame can be transformed to what it would be in another frame.
Consider two frames of reference: [math]\displaystyle{ F }[/math] and [math]\displaystyle{ F' }[/math]. Frame [math]\displaystyle{ F' }[/math] is moving with a constant velocity [math]\displaystyle{ \vec{v} }[/math] relative to [math]\displaystyle{ F }[/math] (meaning [math]\displaystyle{ F }[/math] is moving with a constant velocity [math]\displaystyle{ -\vec{v} }[/math] relative to [math]\displaystyle{ F' }[/math]). A particle has a velocity [math]\displaystyle{ \vec{u} }[/math] in frame [math]\displaystyle{ F }[/math] and a velocity [math]\displaystyle{ \vec{u}' }[/math] in frame [math]\displaystyle{ F' }[/math]. The following relationship exists between [math]\displaystyle{ \vec{u} }[/math] and [math]\displaystyle{ \vec{u}' }[/math]:
[math]\displaystyle{ \vec{u} = \vec{u}' + \vec{v} }[/math].
This equation is the result of the Galilean Transformation Equations, a set of equations that gives the relationship between position vectors in different frames of reference. It should make some amount of intuitive sense. Consider the example mentioned in the "main idea" section: A driver in a car driving north on a highway at 60mph. Let us say frame [math]\displaystyle{ F }[/math] is the road and [math]\displaystyle{ F' }[/math] is the car. [math]\displaystyle{ \vec{v} }[/math], the velocity of [math]\displaystyle{ F' }[/math] relative to [math]\displaystyle{ F }[/math], is therefore 60mph north. It makes geometric sense that the velocity of the driver relative to the road is 60mph north plus the velocity of the driver relative to the car (which for this particular example would be 0 if we assume safe driving habits).
Examples
1. (Simple)
An airplane is flying with a velocity of [math]\displaystyle{ \left \langle {150,20,0} \right \rangle }[/math] km/h relative to the air. It is a windy day, so the air is moving with a velocity of [math]\displaystyle{ \left \langle {-25,0,-10} \right \rangle }[/math] km/h relative to the ground. What is the velocity of the plane relative to the ground?
Solution:
There are two frames of reference in this problem: the air and the ground. We are given the velocity of the plane relative to the air and are asked to find it relative to the ground. Since we are given that the air is moving with velocity [math]\displaystyle{ \left \langle {-25,0,-10} \right \rangle }[/math] km/h relative to the ground, let us call the air [math]\displaystyle{ F' }[/math], making [math]\displaystyle{ \vec{v} }[/math] [math]\displaystyle{ \left \langle {-25,0,-10} \right \rangle }[/math] km/h and [math]\displaystyle{ \vec{u}' }[/math] [math]\displaystyle{ \left \langle {150,20,0} \right \rangle }[/math] km/h.
[math]\displaystyle{ \vec{u} = \vec{u}' + \vec{v} }[/math]
[math]\displaystyle{ \vec{u}_{Airplane/ground} = \left \langle {150,20,0} \right \rangle + \left \langle {-25,0,-10} \right \rangle }[/math]
[math]\displaystyle{ \vec{u}_{Airplane/ground} = \left \langle {125,20,-10} \right \rangle }[/math]
2. (Middling)
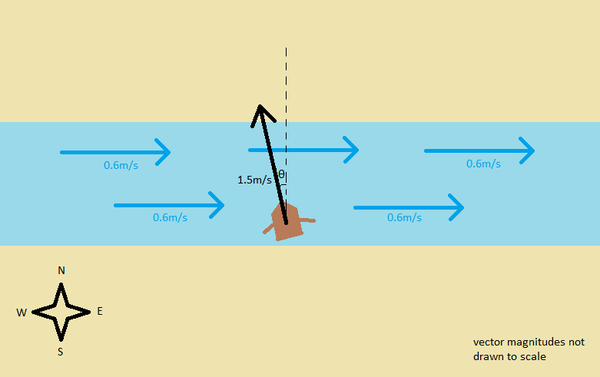
A rower can row their rowboat at a speed of 1.5m/s relative to the water. The rower comes to a straight river flowing to the east at a speed of 0.6m/s. The rower wants to cross the river perpendicularly from south to north. At what angle [math]\displaystyle{ \theta }[/math] west of north should the rower row so that the boat travels in a straight perpendicular line across the river?
Solution:
Let us call east and north the +x and +y directions respectively.
In this problem, there are two frames of reference: the water and the riverbank. Using trigonometry, we can find the velocity of the rowboat relative to the water: [math]\displaystyle{ \left \langle {-1.5\sin\theta,1.5\cos\theta} \right \rangle }[/math].
Now, by the formula