Speed vs Velocity
This is a short page aiming to differentiate between speed and velocity. For more detailed information on either of those topics, view their respective main pages.
The Main Idea
Speed ([math]\displaystyle{ v }[/math]) and velocity ([math]\displaystyle{ \vec{v} }[/math] or v) are similar concepts, and as a result, the terms are often confused and interchanged incorrectly in everyday conversation. The key difference between them is that velocity is a vector quantity that describes both how fast and in which direction an object is moving, while speed is a scalar quantity that describes only how fast an object is moving. Speed is the magnitude of the velocity vector. Velocity is the more descriptive of the two, as it contains all of the information speed contains and then some. It is easy to tell the speed of an object given only its velocity, but it is impossible to tell the velocity of an object given only its speed because one has no way of knowing the object's direction of travel.
Both speed and velocity have the same units because a vector always has the same units as its magnitude. Both are measured in units of distance over units of time. The SI unit for both speed and velocity is the meter per second (m/s). Both speed and velocity are instantaneous values and can change over time.
Mathematical Relationship Between Speed and Velocity
The following formulas describe the relationship between speed and velocity and can be helpful when converting between the two:
[math]\displaystyle{ v = |\vec{v}| }[/math]
[math]\displaystyle{ v = \sqrt{v_x^2 + v_y^2 + v_z^2} }[/math] (in 3 dimensions)
[math]\displaystyle{ \vec{v} = v\hat{v} }[/math], where [math]\displaystyle{ \hat{v} }[/math] is the direction of travel
Average Speed vs Average Velocity
One of the biggest sources of confusion between speed and velocity is the difference between average speed and average velocity. This is because although instantaneous speed is the magnitude of instantaneous velocity, average speed may not be the magnitude of average velocity. To understand why, let us take a look at the following formulas:
[math]\displaystyle{ \vec{v}_{avg} = \frac{\Delta \vec{r}}{\Delta t} }[/math]
where [math]\displaystyle{ \Delta \vec{r} }[/math] is the displacement (change in position) over that time interval ([math]\displaystyle{ \Delta \vec{r} = \vec{r}_f - \vec{r}_i }[/math]).
[math]\displaystyle{ v_{avg} = \frac{\Delta s}{\Delta t} }[/math]
where [math]\displaystyle{ \Delta s }[/math] is the distance traveled during the time interval [math]\displaystyle{ \Delta t }[/math].
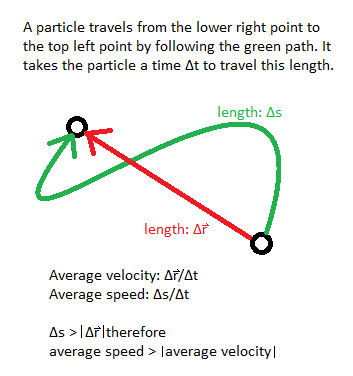
The difference lies in the fact that the magnitude of the displacement of a moving particle over a specific time interval may not equal the distance it traveled during that time interval. The displacement of the particle is merely the difference between its final and initial positions, and its magnitude is simply the straight line distance between those points. It does not depend on the path taken by the particle to get between those positions. The distance traveled, however, is the length of the path taken by the particle. The magnitude of the displacement of a moving particle over a specific time interval only equals the distance it traveled during that time interval if it traveled in a straight line for the duration of the interval. If there are any curves or turns, the distance traveled by the particle is greater than its displacement, so the particle's average speed is greater than the magnitude of its average velocity.
In the above image, it makes sense that the magnitude of the particle's average velocity is lower than its average speed because the particle's velocity at certain points in time partially cancels with its velocity at other points in time.
Examples
1. (Simple)
A particle is moving with a velocity of <4,-4,7>m/s. What is the particle's speed?
Solution:
[math]\displaystyle{ v = |\vec{v}| = \sqrt{4^2 + (-4)^2 + 7^2} = 9 }[/math]m/s.
2. (Simple)
A runner runs a 560m lap around a circular track in 200s. Do not assume that the runner's speed is constant.
a) What is the average speed of the runner over the course of the lap?
b) What is the average velocity of the runner over the course of the lap?
Solutions:
a) To find the average speed of the runner, let us use the following formula:
[math]\displaystyle{ |v|_{avg} = \frac{\Delta s}{\Delta t} }[/math]
[math]\displaystyle{ |v|_{avg} = \frac{560}{200} }[/math]
[math]\displaystyle{ |v|_{avg} = 2.8 }[/math]m/s
b) To find the average value of the velocity vector over time, let us use the following formula:
[math]\displaystyle{ \vec{v}_{avg} = \frac{\Delta \vec{r}}{\Delta t} }[/math].
Because the runner ran a single lap and ended at the point in space where they began, their displacement [math]\displaystyle{ \Delta \vec{r} }[/math] was <0,0>m! The runner's average velocity was therefore <0,0>m/s. This makes sense because the velocity vector spends time pointing in every possible direction in the plane of the track, so each instantaneous velocity at any point along the track cancels with other instantaneous velocities at other points along the track.
3. (Middling)
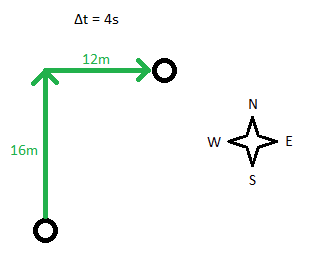
Over the course of 4s, a particle moves 16m in the northward direction, then 12m in the eastward direction.
a) What is the particle's average speed?
b) What is the magnitude of the particle's average velocity?
Solutions:
a) Let us use the following formula:
[math]\displaystyle{ v_{avg} = \frac{\Delta s}{\Delta t} }[/math]
[math]\displaystyle{ \Delta s }[/math] is the length of the path traveled by the particle, which in this case is 16 + 12 = 28m.
[math]\displaystyle{ v_{avg} = \frac{28}{4} }[/math]
[math]\displaystyle{ v_{avg} = 7 }[/math]m/s.
b) Let us use the following formula:
[math]\displaystyle{ \vec{v}_{avg} = \frac{\Delta \vec{r}}{\Delta t} }[/math]
[math]\displaystyle{ \Delta \vec{r} }[/math] is the displacement vector of the particle, which in this case is <16,12>m.
[math]\displaystyle{ \vec{v}_{avg} = \frac{\lt 16,12\gt }{4} }[/math]
[math]\displaystyle{ \vec{v}_{avg} = \lt 4,3\gt }[/math]m/s.
We are asked to find the magnitude of the particle's average velocity, so let us use the Pythagorean theorem:
[math]\displaystyle{ |\vec{v}_{avg}| = \sqrt{4^2 + 3^2} }[/math]
[math]\displaystyle{ |\vec{v}_{avg}| = \sqrt{25} }[/math]
[math]\displaystyle{ |\vec{v}_{avg}| = 5 }[/math]m/s.
Note that [math]\displaystyle{ |\vec{v}_{avg}| \lt v_{avg} }[/math].
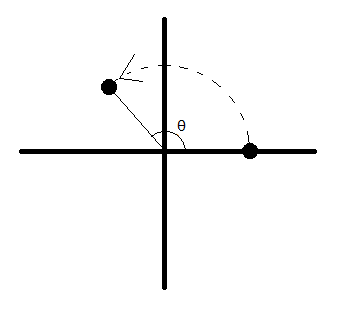
4. (Difficult)
A particle lies on the +x axis and travels counterclockwise along a circular path centered on the origin. Over some time interval [math]\displaystyle{ \Delta t }[/math], the particle has an average speed of 14m/s and an average velocity with a magnitude of 11m/s. What is the angle of the arc [math]\displaystyle{ \theta }[/math] traveled by the particle? Hint: use of an equation solver is necessary.
Solution:
[math]\displaystyle{ v_{avg} = \frac{\Delta s}{\Delta t} }[/math]
and
[math]\displaystyle{ |\vec{v}_{avg}| = \frac{|\Delta \vec{r}|}{\Delta t} }[/math]
Therefore
[math]\displaystyle{ \frac{v_{avg}}{|\vec{v}_{avg}|} = \frac{\frac{\Delta s}{\Delta t}}{\frac{|\Delta \vec{r}|}{\Delta t}} = \frac{\Delta s}{|\Delta \vec{r}|} }[/math]
In this problem, we are told that [math]\displaystyle{ \frac{v_{avg}}{|\vec{v}_{avg}|} = \frac{14}{11} }[/math], so [math]\displaystyle{ \frac{\Delta s}{|\Delta \vec{r}|} = \frac{14}{11} }[/math] as well.
Let us find [math]\displaystyle{ \Delta s }[/math] and [math]\displaystyle{ |\Delta \vec{r}| }[/math] as functions of [math]\displaystyle{ \theta }[/math] so we can see at what value of [math]\displaystyle{ \theta }[/math] they have the ratio 14:11.
Let us call the radius of the circular path [math]\displaystyle{ R }[/math].
[math]\displaystyle{ \Delta s (\theta) = R \theta }[/math]
[math]\displaystyle{ |\Delta \vec{r}| = \sqrt{(R-R\cos \theta)^2 + (R\sin \theta)^2} }[/math] ([math]\displaystyle{ R-R\cos \theta }[/math] is the magnitude of the horizontal component of [math]\displaystyle{ \vec{r} }[/math], while [math]\displaystyle{ R\sin \theta }[/math] is the magnitude of the vertical component)
This simplifies to
[math]\displaystyle{ |\Delta \vec{r}| = R\sqrt{(1-\cos \theta)^2 + (\sin \theta)^2} }[/math]
Now let us find the value of [math]\displaystyle{ \theta }[/math]:
[math]\displaystyle{ \frac{\Delta s}{|\Delta \vec{r}|} = \frac{14}{11} = \frac{R \theta}{R\sqrt{(1-\cos \theta)^2 + (\sin \theta)^2}} = \frac{\theta}{\sqrt{(1-\cos \theta)^2 + (\sin \theta)^2}} }[/math]
It is impossible to solve for [math]\displaystyle{ \theta }[/math] algebraically so let us use an equation solver.
[math]\displaystyle{ \theta = 2.35 }[/math]rad
See also
External links
The Physics Classroom: Speed and Velocity
References
Matter and Interactions, Modern Mechanics, Volume One 4th Edition by Chabay and Sherwood.