Heisenberg Uncertainty Principle

Claimed by Nicholas Maldonado 11/27/22

Heisenberg Uncertainty Principle

The Heisenberg uncertainty principle is a concept that describes uncertainty relationships between a particle's different properties, those being position and momentum, as well as energy and time.The biggest takeaway from this concept is that there is always some measure of uncertainty in at least one of any given particle's properties.

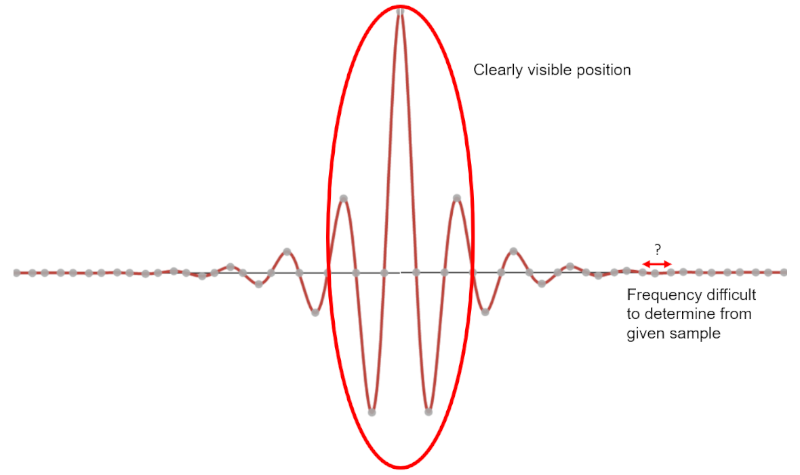
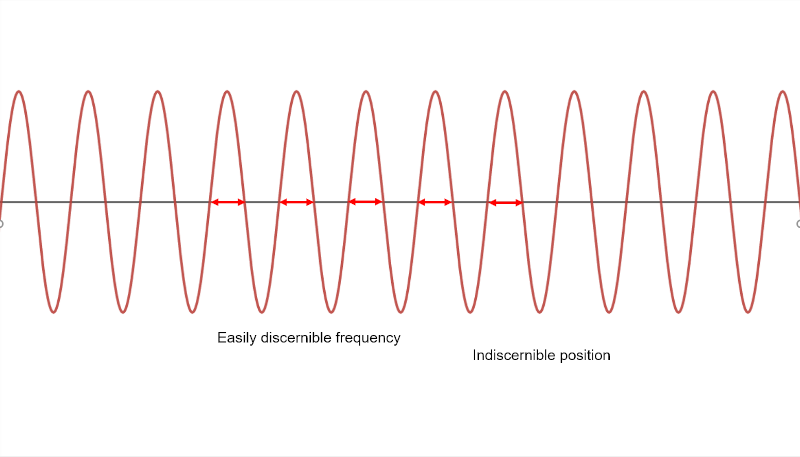
Generally speaking, uncertainty relationships are not unique to modern physics. This is a concept that occurs in classical physics as well. Consider a wave, described by some combination of sines and cosines. Any wave has an amount of uncertainty between its frequency and its position. For example, a wave with a single period would give you a lot of information about its position, but not much information about its frequency. Conversely, a wave of many periods would allow you to precisely determine its frequency, but the position of the wave would be less certain.

However, why would a particle obey this principle that appears to apply only to waves? Notice that objects at the quantum scale actually exhibit Wave-Particle Duality. Anything with a mass, including objects classically thought as discrete particles, have an associated wavelength. What this wave is exactly relates to the particle's position, which is innately probabilistic. The Uncertainty Principle naturally follows the result that this wavelength is dependent on a particle's momentum.

A Mathematical Model

An adequately rigorous derivation of the Heisenberg Uncertainty Principle requires knowledge in the mathematics governing quantum mechanical systems, namely linear algebra with abstract vector spaces. A high-level overview of the mathematics is instead given:

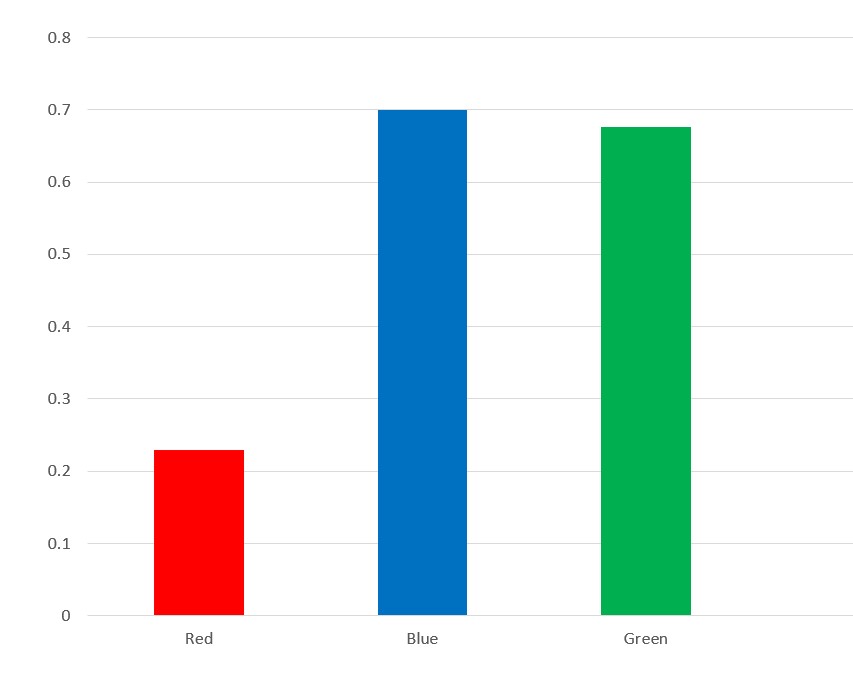
A quantum system, which in this case can be a single particle, is represented by a "state vector". The components of this vector contain information on the probabilities associated with measurements. Each "dimension" of this vector corresponds to a possible outcome, and the magnitudes of the vector along each dimension indicates the likelihood the particle will be found in the corresponding state.

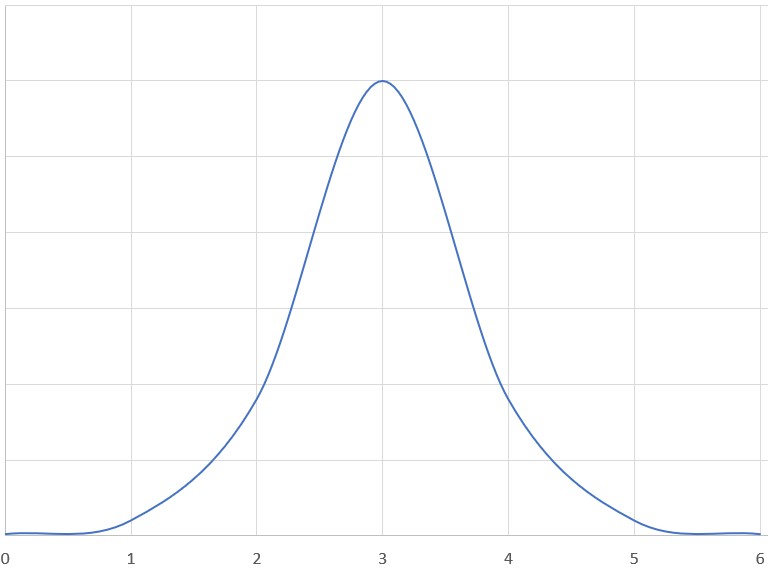
Above is a graph depicting the components of a quantum state vector. Each component corresponds to an outcome of a measurement, which in this case is the fictitious property "color". It is evident that it is more likely the particle will be found to be "blue" rather than "red" or "green". Below is a graph depicting the components of a state vector for a continuous property, like position. Every point on the curve corresponds to a component of the vector (it has an infinite number of dimensions). For example, the value at the x-value 3.32 gives us information on the likelihood the particle will be found around x=3.32.

An actual quantum state vector actually takes complex values for its components. It would be more accurate to add another dimension to both of the above graphs, indicating the imaginary part of each component. This has been omitted for simplicity.

The measurement of some property amounts to acting on this vector with an "operator". Every measurable quantity, like position, momentum, energy, and even angular momentum can be paired with a corresponding operator. What is important is the fact operators can alter the components of the vector, and thus the particle itself. It is not physically possible to measure two entirely distinct quantities at once, so measuring position and momentum means applying one operator and then another (or vice versa). It is then easy to see that the order of application matters. The way two operators can alter (or preserve) a particle's state is summarized by a mathematical object called the commutator. For two objects [math]\displaystyle{ {\hat{A}} }[/math] and [math]\displaystyle{ {\hat{B}} }[/math], the commutator is given by

[math]\displaystyle{ {\hat{A}\hat{B}-\hat{B}\hat{A}} }[/math].

Notice that this is not zero, as the order of the operators matter! From this the minimum uncertainty introduced in one property by the measurement of another property can be found.

The total uncertainty between a particle's position and momentum is given as [math]\displaystyle{ {\Delta p \Delta x} }[/math]. The minimum uncertainty a particle can have is [math]\displaystyle{ {\frac{{\hbar}}{2}} }[/math]. Therefore, we can establish the relationship of:

[math]\displaystyle{ {\Delta p \Delta x \geq \frac{{\hbar}}{2}} }[/math]

Oftentimes, it is also good enough to simply approximate their general relationship as:

[math]\displaystyle{ {\Delta p \Delta x} }[/math] ~ [math]\displaystyle{ {\hbar} }[/math]

NOTE: [math]\displaystyle{ {\hbar = \frac{{h}}{2\pi}} }[/math] where [math]\displaystyle{ {h} }[/math] is Planck's constant.

This principle can also be extended to a relationship between energy and time, where:

[math]\displaystyle{ {\Delta E \Delta t \geq \frac{{\hbar}}{2}} }[/math]

and

[math]\displaystyle{ {\Delta E \Delta t} }[/math] ~ [math]\displaystyle{ {\hbar} }[/math]

A Computational Model

TODO: ADD COMPUTATIONAL MODEL

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Examples

TODO: ADD EXAMPLES

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

A particle is confined to a box 0.1 nm wide. Estimate the minimum uncertainty of its momentum.

Solution: The minimum uncertainties are related by [math]\displaystyle{ {\Delta x \Delta p \geq \hbar/2} }[/math]. Taking the uncertainty of the particle's position to be the width of the box, the uncertainty of the momentum is then

<math> {\Delta p \geq \frac{\hbar}{2\Delta x}\approx 5.27\times 10^-25} </mat> kg m/s.

Middling

Difficult

Connectedness

The Heisenberg uncertainty principle later plays into quantum tunneling, where this inherent uncertainty in a particle may sometimes allow it to overcome a potential energy barrier it otherwise would not be able to overcome classically (see Quantum Tunneling through Potential Barriers).
As a consequence of Heisenberg uncertainty principle, microelectronics are limited in size because electrons are able to tunnel through transistors that are small enough for uncertainty principle to have an effect.
Hydrogen nuclei are positively charged, so bringing two of them close enough together to fuse requires passing an Electric Potential. This takes a large amount of kinetic energy, corresponding to a temperature much higher than the cores of most stars. Tunneling allows particles with much lower kinetic energies to fuse. In other words, without tunneling, stars including our sun would produce no energy at all!

History

The development of the Heisenberg uncertainty principle is largely accredited to Werner Heisenberg.e

Single-slit Diffraction Experiments

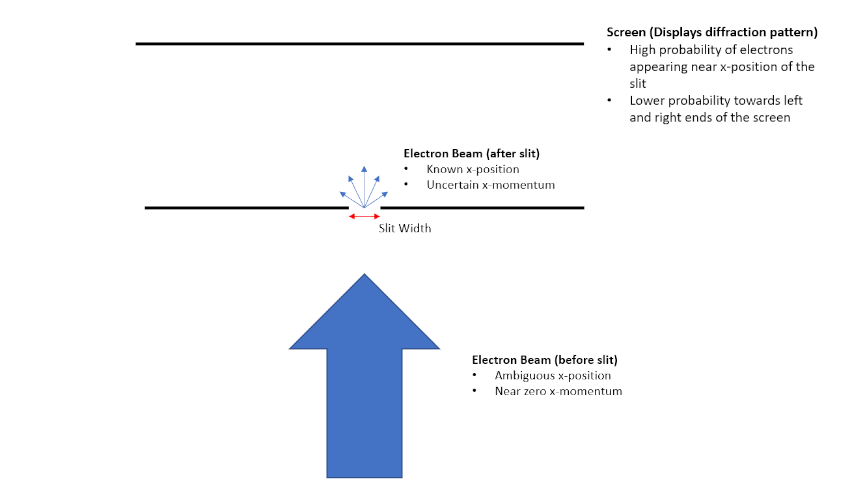
Heisenberg uncertainty relationships were first physically demonstrated through single-slit diffraction experiments. The experiment is conducted by launching beam of electrons through a narrow slit. Initially, the electrons have zero momentum in the x-direction. After passing through the slit, information about an electron's x position is acquired, resulting in an increased uncertainty in the particle's x momentum. Making the slit narrower therefore increases the uncertainty of the particle's x momentum while decreasing the uncertainty of its x position, while making the slit wider has the opposite effect. This effectively demonstrates the relationship between the uncertainty of a particle's position and momentum.

The Uncertainty Principle. Uncertainty principle. (n.d.). Retrieved April 20, 2022, from hyperphysics.phy-astr.gsu.edu

Libretexts. (2021, April 23). Heisenberg's Uncertainty Principle. Chemistry LibreTexts. Retrieved April 20, 2022, from chem.libretexts.org

Heisenberg Uncertainty Principle

Contents