Conductivity and Resistivity

'This page was constructed from an amalgamation of Conductivity and Resistivity, then edited by Elizabeth Pettit, Fall 2020'

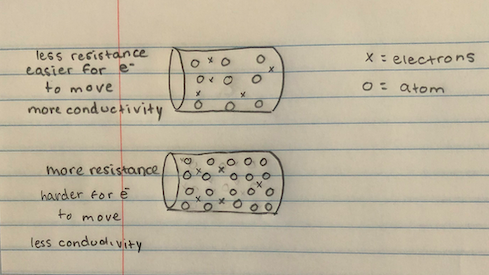
Conductivity is the degree to which a specified material conducts electricity, calculated as the ratio of the current density in the material to the electric field that causes the flow of current. Resistivity is the reciprocal of conductivity, and so the two are interchangeable as long as one tracks the inversions (and, correspondingly, the units). Electrical conductivity tells us how well a material will allow electricity to travel through it, and is similar to thermal conductivity, which tells us the ease with which thermal energy (heat for most purposes) can move through the material.

Main Idea

A conductor is a material which gives very little resistance to the flow of an electric current. The resistivity of a material is not just dependent on the free electrons in the material but it is also dependent on the temperature at which the object is held at.

Correspondingly, an insulator is a material which is very resistant to the flow of electric current. Semiconductors are materials which display the properties of both conductors and insulators. The most common example of conductive materials are metals, while insulators include materials such as wood or plastics . Semiconductors are generally more rare, but are necessary for the construction of transistors, and as such are present in all computers, with the most common being doped silicon. In addition to these categories, there are superconductors, which have zero resistance under certain conditions (generally extremely low temperatures and/or extremely high pressures), and there also exist a host of other materials with odd behaviors.

The units for conductivity and resistivity are most naturally expressed in terms of the recognizable Ohm ([math]\displaystyle{ \Omega }[/math]). Resistivity has units of [math]\displaystyle{ \Omega \cdot m }[/math], so conductivity has units of [math]\displaystyle{ \frac{1}{\Omega \cdot m} }[/math]. Expressed in terms of SI base units, the unit of resistivity becomes [math]\displaystyle{ \frac{kg\cdot m^3}{s^3\cdot A^2} = \frac{kg\cdot m^3}{s\cdot C^2} }[/math].

~temperature the material is held in

~concentrations of ions (an electrolyte moves through water carrying electrical currents.

~type of ions

~ if rock, pore saturation

Mathematical Method

First, we have the relation between conductivity and resistivity:

[math]\displaystyle{ \sigma = \frac{1}{\rho} }[/math]

By convention, we have [math]\displaystyle{ \sigma }[/math] as the conductivity, and [math]\displaystyle{ \rho }[/math] as the resistivity.

Resistivity geometry

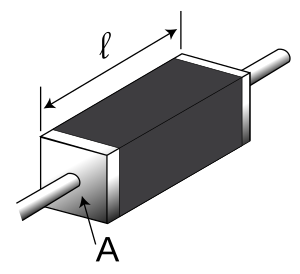
Conductivity and Resistivity are properties of a material, dependent primarily on its chemical composition and structure, but also on its temperature and other environmental factors. As such, for our purposes it will always be either a know value, plugged into an equation, or an unknown value, derived from that equation. Our interest is therefore in those equations. The first is on the idealized relation between resistivity and resistance:

[math]\displaystyle{ R = \frac{\rho L}{A} }[/math]

In this, resistance is [math]\displaystyle{ R }[/math], the length of the wire is [math]\displaystyle{ L }[/math], [math]\displaystyle{ rho }[/math] is equal to resistivity and the variable [math]\displaystyle{ A }[/math] is its cross sectional area. This assumes that there is a clearly defined length (parallel to the direction of current flow) and cross sectional area (perpendicular to the direction of current flow).

Area of a conductor can be adjusted by making additional connections to the conductor in a circuit. For example, If you had a current pointing from North to South, by attaching a second conductor parallel to the first one the area. of the conductor would be doubled.

As seen by the equation [math]\displaystyle{ R = \frac{\rho L}{A} }[/math], doubling the Area would cut the resistance in half and effectively double the conductance of the circuit containing the conductors seeing that [math]\displaystyle{ \sigma = \frac{1}{\rho} }[/math]

Naturally, this is exactly the scenario present in a standard wire. The next two relevant equations are two statements of the same fact, which we call Ohm's law. Precisely, it governs the relationship between the flow of charge and the electric field which produces that flow. The first form states this explicitly:

Through this equation, the "skin effect" is produced.

The "skin effect" consists of an explanation for the relationship between the current density and the radius of a wire. It explains that the thicker the wire (the bigger the radius), the larger the current density.

[math]\displaystyle{ \vec{J} = \sigma \vec{E} }[/math]

Here [math]\displaystyle{ \vec{J} }[/math] is the current density, and [math]\displaystyle{ \vec{E} }[/math] is the electric field as we've seen before. An aside on current density: it is the amount of charge which passes through a given cross sectional area in a given period of time, with SI units [math]\displaystyle{ \frac{A}{m^2} = \frac{C}{m^2 \cdot s} }[/math]. This means that it is a density with area in the denominator, which can be confusing. Given what one has learned so far, this is the operable definition of Ohm's Law. However, another version is more frequently used later on, and so will also be given here:

[math]\displaystyle{ V = I R }[/math]

where [math]\displaystyle{ V }[/math] is the electric potential, [math]\displaystyle{ I }[/math] is the current, and [math]\displaystyle{ R }[/math] is resistance as defined before.

Computational Method

This topic is largely conceptual and algebraic, so there is relatively little modeling to be done. However, this program is designed to create plots of the relationship between resistance, resistivity, length and cross sectional area.

Resistance and length across different fixed points

Resistance and area across different fixed points

Furthermore, this external program provides a good visual demonstration of the relationship (but unfortunately the source code is not accessible).

Examples

Simple

Example Number 1

A semi conductive material has a resistivity of [math]\displaystyle{ 200 \; \Omega\cdot m }[/math]. What is its conductivity?

Solution

Since conductivity is the reciprocal of resistivity,

[math]\displaystyle{ \sigma = \frac{1}{\rho} = \frac{1}{200 \; \Omega \cdot m} = 0.005 \frac{1}{\Omega \cdot m} }[/math]

Example Number 2 A unknown material is used in the creation of a video game console.

Part A: How would the amount of free electrons in the material affect the conductance of the material?

Part B:Would the materials conductance increase or decrease if you put the material in the freezer as opposed to room temperature?

Solution For Part A

Because the more free electrons, the less resistance a material has and since [math]\displaystyle{ \sigma = \frac{1}{\rho} }[/math], there is an obvious inverse relationship between resistivity and conductance. This means that the more free electrons, the less resistance, and therefore the more conductance an object will have.

Solution For Part B

Temperature increases cause free electrons to move quicker in any material. If free electrons move quicker, the resistance of the object decreases and the conductance of the material would increase. This implies that the material will transfer heat and or energy slower because the material was moved to a colder environment, decreasing the speed of the free electrons, increasing resistivity, and decreasing conductance of the material.

Middling

Example Number 1 An electric potential of [math]\displaystyle{ 120 V }[/math] is applied to a circular wire of length [math]\displaystyle{ 2 \cdot 10^4 \; m }[/math] and radius [math]\displaystyle{ 0.001 m }[/math]. The current is equal to [math]\displaystyle{ 1.11 \; A }[/math]. Determine the resistivity, and match it to an elemental metal using an appropriate table (such as )

Solution

We have Ohm's Law

[math]\displaystyle{ V = I R }[/math]

and so plugging in our definition for resistance in terms of resistivity gives that

[math]\displaystyle{ V = \frac{I \rho L}{A} }[/math]

which we rearrange to get

[math]\displaystyle{ \rho = \frac{ V A}{I L} }[/math]

plugging all of the values in gives an answer of [math]\displaystyle{ \rho = 1.7 \cdot 10^{-8} \; \Omega \cdot m }[/math], which is the resistivity of copper.

Example Number 2

A student wishes to cut a wire in order to reach a specific potential difference.

Given what we know about Ohm's law, a student discovers that the wire she is using in a circuit to light a light bulb has a resistance of [math]\displaystyle{ \rho = 2.0 \cdot 10^{-7} \; \Omega \cdot m }[/math] and a radius of .002 meters. The current in the circuit is equal to 1 Amepere. The student then realizes that in order for the light bulb to be lit, there must be an electric potential across the light bulb of at least 100 Volts. Given that there are no other resistors in the circuit, determine the necessary length of the wire that she would need to cut in order for the potential difference of the wire to equal 100 Volts.

Solution

We can start by rearranging Ohm's Law

Ohms Law is equal to

[math]\displaystyle{ V = I R }[/math]

and so plugging in our definition for resistance in terms of resistivity gives that

[math]\displaystyle{ V = \frac{I \rho L}{A} }[/math]

which we rearrange to get

[math]\displaystyle{ \rho = \frac{ V A}{I L} }[/math] like in example 1

If the equation is even more rearranged in order to find the necessary length she needs to cut of the wire to get a potential difference, the equation would be

[math]\displaystyle{ L= \frac{ V* A}{I*rho} }[/math]

The next step is to use the radius of the wire in the given problem to find the area

Area= pi*r^2

If you plug in the numbers you get [math]\displaystyle{ L=100*(pi*(.002)^2)/(2.0 \cdot 10^{-7}*1)\lt \math\gt This gives you a necessary length of 6.28 \cdot 10^{5} meters \lt /div\gt \lt /div\gt ===Difficult=== One cubic meter of a fictional material with resistivity \lt math\gt \rho = 10^{-5} \; \Omega \cdot m }[/math] is formed into a shape with uniform cross sectional area (such that volume is equal to the base times the height) for which the resistance to current run lengthwise is equal to [math]\displaystyle{ 10 \; \Omega }[/math]. Determine the dimensions (length and cross sectional area) of the shape, presuming that it follows Ohm's law and the equation for resistance given above.

Solution

As the clarification hints, it is necessary to use a little basic geometry to solve this problem, namely

[math]\displaystyle{ V = L \cdot A }[/math]

So we lay out the standard formula

[math]\displaystyle{ R = \frac{\rho L}{A} }[/math]

Then multiply both numerator and denominator by [math]\displaystyle{ L }[/math] to obtain

[math]\displaystyle{ R = \frac{\rho L^2}{A L} = \frac{\rho L^2}{V} }[/math]

From here it is simply rearrangement to find that

[math]\displaystyle{ L = \sqrt{\frac{R V}{\rho}} = \sqrt{\frac{(1 \;m^3)(10 \;\Omega)}{10^{-5} \; \Omega \cdot m }} = 10^2 \; m }[/math]

With the length determined, it is then straightforward to conclude that [math]\displaystyle{ A = 10^{-2} \; m^2 }[/math], and the cross-section can take any shape which has that enclosed area.

Connectedness

Every time an electrical system has been created, an understanding of conductivity and resistivity had to be determined.

since conductivity and resistivity are related, it is reasonable to assume that wires or components with low electric resistivity make good conductors as they have a great ability to transmit electricity and heat and wires or components with high electric resistivity make bad conductors.

This is important in many real life applications, some of which include:

Home insulation: materials with high resistivity so the temperature of your house is maintained.

Cooking: Pots, pans, and other metallic objects are used to cook food. This is because the food is placed on the pan, which due to its low resistivity resulting from the metal's free electrons. As the resistivity is low, there is high conductivity and the heat from a stove would be able to easily reach the food on the pan without having to place the food directly onto the stove's surface.

Electronic Devices: Electronic devices rely on the transportation of currents to create electricity that powers the device. However, one problem with many electronic devices is they are prone to overheating. In order to regulate the temperature created by the constant usage of energy in the device, materials in the machine can be surrounded or replaced with highly resistive materials to slow the conductance of the current.

Measuring Conductivity

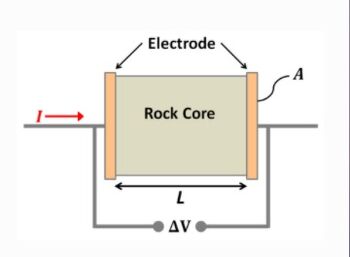
To measure conductivity, a sample of the material is placed in between two metallic electrodes, either made of copper or granite. Ohm's law is then used to calculate the numerical value of the resistance of the circuit.

This is done through monitoring the current that is produced from the loop and the [math]\displaystyle{ delta V }[/math] that can be measured through the attachment of an ammeter to the copper or granite circuit. The stronger conductors would have a higher <health>delta V<delta V> value and/or a lower I, a larger convection current.

History

The first scientist to contribute substantially to the study of conductivity and resistivity was Stephen Gray, who with his friend Ganvil Wheler noticed that electricity could be transmitted a distance, and that the effectiveness of this transmission varied between a wire of silk and wire of brass . A substantial amount of discovery then followed, including the famous contributions of Benjamin Franklin, but these developments are more relevant to other subjects.

It was in the early 19th century that the equation for determining resistance from resistivity and geometry was determined by Antoine Becquerel (grandfather to Henri Becquerel, who was a pioneer in radioactivity alongside Marie Skłodowska Curie and Pierre Curie). Not long after, Georg Ohm proposed an incorrect theorem for the relation between current, potential and resistance, then soon amended it to the correct formula. The correction, philosophical differences, and confusion at the time about the definitions of resistance, current and potential led his work to be poorly received at first, but ultimately accepted and celebrated about 15 years after its release.

See Also

If you are interested in learning more about this topic or want further clarification about concepts, check out these resources!

Further reading

The textbook Matter and Interaction by Chabay and Sherwood has some discussion of conductivity and resistivity:

• Chapter 14 discusses conductors and insulators with some specifics about polarization and charge. Page 548 includes a specific definition for both.
• Page 771 talks about conductivity
• Page 773 talks about resistance in relation to conductivity and geometry
• Page 775 talks about semiconductors

The textbook Electricity and Magnetism by Purcell also covers conductivity and resistivity:

• Chapter 3.1 covers conductors and insulators
• Chapter 4.6 covers semiconductors

External links

• Table of electrical resistivity and conductivity values for different materials: https://www.thoughtco.com/table-of-electrical-resistivity-conductivity-608499
• Resistivity and conductivity explanation: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/resis.html
• Khan Academy video on resistivity and conductivity https://www.khanacademy.org/science/ap-physics-1/ap-circuits-topic/current-ap/v/resistivity-and-conductivity
• Resistivity, An explanation (Youtube Video By Brian Swarthout) https://youtu.be/dRtNvUQC7c8

References