Conductivity and Resistivity

'This page was constructed from an amalgamation of Conductivity and Resistivity, then edited by Islombek Kadirov, Fall 2023'

In the field of electrical engineering and materials science, conductivity refers to the ability of a material to conduct electric current. It is quantitatively measured as the ratio of the current density to the electric field causing the current flow. This property varies among different materials, significantly influencing their applications in various industries.

Resistivity, on the other hand, is the inverse of conductivity. It quantifies how strongly a material opposes the flow of electric current. The relationship between resistivity and conductivity is reciprocal, allowing for interchangeability in calculations and analyses, provided the inverse nature and corresponding units are properly accounted for.

Electrical conductivity is a measure of a material's capability to allow the passage of electric current. It indicates how easily electricity can traverse through a given material. This concept is analogous to thermal conductivity, which determines the efficiency with which thermal energy, commonly in the form of heat, can move through a material. Both electrical and thermal conductivity provide crucial insights into the behavior of materials under different energy transfer scenarios, making them fundamental properties in various fields, including materials science, electrical engineering, and thermal engineering.^[1].

Main Idea

^[2]

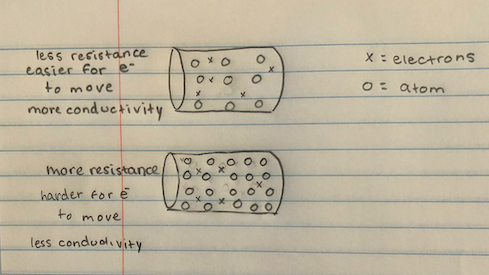
In the accompanying image, the interrelated nature of conductance and resistance is visually represented, illustrating how various factors influence these electrical properties. The image exemplifies how the density of atoms within a material can impact the movement of electrons. This visual aid serves to demonstrate the effect of atomic density on electron mobility, thereby affecting the material's conductance and resistance.

In the first material depicted, the atoms are more widely spaced, providing a greater area for the movement of free electrons. This phenomenon is identified as resistance. The conductance of the material is influenced by the transfer of these free electrons; a higher rate of free electron passage in a given timeframe correlates with increased conductivity. Due to the pronounced movement of free electrons, this material demonstrates lower resistance and higher conductivity, making it more efficient in transferring heat or energy. Consequently, it is often utilized as a conductor.

In the second material, the atoms are positioned closer together, resulting in reduced space for the movement of free electrons, a characteristic known as resistance. The conductance of this material is consequently affected by the limited transfer of free electrons. The fewer free electrons that pass through within a given timeframe, the less conductive the material is. Due to this diminished movement of free electrons, the material exhibits greater resistance and reduced conductivity, leading to less efficient heat or energy transfer. Such properties render this material more suitable for use as an insulator.

A conductor is a type of material that offers minimal resistance to the flow of electric current, making it highly efficient for conducting electricity. It's important to note that the resistivity of a material is influenced not only by the presence of free electrons but also by the temperature at which the material is maintained. Variations in temperature can significantly alter a material's resistive properties, affecting its ability to conduct electricity. This interplay between electron mobility and temperature is a crucial factor in determining the overall conductive or resistive behavior of a material.

An insulator is a material that exhibits high resistance to the flow of electric current, effectively preventing or significantly hindering the passage of electricity. Semiconductors, on the other hand, are materials that possess properties of both conductors and insulators, allowing them to conduct electricity under certain conditions. Common examples of conductive materials include metals, known for their low resistivity and high conductivity. Insulators typically comprise materials like wood or plastics, which have high resistivity and are used to prevent unwanted flow of electric current ^[3]. Semiconductors, though more rare compared to conductors and insulators, play a crucial role in modern technology, particularly in the construction of transistors. These components are essential in all computers and a wide range of electronic devices. The most commonly used semiconductor material is doped silicon, which, through the process of doping, acquires the necessary electrical properties to efficiently control and amplify electronic signals. This characteristic makes semiconductors indispensable in the realm of digital electronics and integrated circuits ^[4]. Beyond conductors, insulators, and semiconductors, there is another notable category known as superconductors. The phenomenon of superconductivity, discovered in 1911, is a quantum mechanical marvel that allows for the unimpeded flow of electric current, making superconductors highly valuable for applications requiring efficient energy transmission, powerful electromagnets, and advanced technologies like magnetic resonance imaging (MRI) and particle accelerators, and these unique materials exhibit zero electrical resistance under specific conditions, typically at extremely low temperatures and/or under high pressures ^[5], and there also exist a host of other materials with odd behaviors.

Units For Conductivity and Resistivity:

The units used to express conductivity and resistivity are indeed based on the familiar Ohm, a unit of electrical resistance. Conductivity, which measures how easily a material allows the flow of electric current, is typically expressed in Siemens per meter (S/m). On the other hand, resistivity, representing how much a material resists the flow of electric current, is measured in ohm-meters (Ω·m). These units provide a standardized way to quantify and compare the electrical properties of different materials, crucial for applications in electrical engineering and materials science. Expressed in terms of SI base units, the unit of resistivity becomes [math]\displaystyle{ \frac{kg\cdot m^3}{s^3\cdot A^2} = \frac{kg\cdot m^3}{s\cdot C^2} }[/math].

Factors that influence the resistivity of an object:

~Material Composition: Different materials inherently have different levels of resistivity. For instance, metals typically have lower resistivity than insulators like plastic or wood.

~Temperature: Generally, for conductors, resistivity increases with temperature. In semiconductors and insulators, the effect can be more complex.

~Impurities and Material Defects: The presence of impurities and defects in a material can significantly alter its resistivity. This is particularly notable in semiconductors, where doping with impurities is used to control resistivity.

~ Physical Structure: The microscopic structure of a material, including its crystal structure and the presence of grain boundaries, can affect resistivity.

~Pressure: Applying pressure to a material can change its resistivity, though this effect is generally less significant than temperature or material composition.

Mathematical Method

The relationship between conductivity and resistivity is a fundamental concept in the field of materials science and electrical engineering. Here's how they are related:

[math]\displaystyle{ \sigma = \frac{1}{\rho} }[/math]

By convention, we have [math]\displaystyle{ \sigma }[/math] as the conductivity, and [math]\displaystyle{ \rho }[/math] as the resistivity.

Conductivity and Resistivity are intrinsic material properties, influenced primarily by chemical composition and structural attributes, but also sensitive to temperature and other environmental conditions. In practical applications, these values are either predetermined constants used in calculations or derived outcomes from specific equations. The focus thus lies in understanding the relevant equations that govern these properties. A key equation relates resistivity to resistance in an idealized manner, providing a foundational understanding for analyzing the electrical characteristics of different materials. This relationship is crucial for the design and analysis of electrical and electronic systems, where accurate knowledge of material properties is essential.

[math]\displaystyle{ R = \frac{\rho L}{A} }[/math]

In this context, the resistance of a wire is denoted as [math]\displaystyle{ R }[/math], the length of the wire is [math]\displaystyle{ L }[/math], [math]\displaystyle{ rho }[/math] is equal to resistivity and the variable [math]\displaystyle{ A }[/math] is its cross sectional area. This formulation presupposes a well-defined length of the wire aligned with the direction of electric current flow and a specific cross-sectional area perpendicular to the current's direction. These parameters are essential in determining the wire's resistance characteristics, especially in the context of electrical and electronic engineering.

Adjusting the area of a conductor can be achieved by making additional connections to it within a circuit. For instance, if there is a current flowing from North to South through a conductor, attaching a second conductor parallel to the first effectively doubles the area of the conductor. This modification impacts the overall resistance of the circuit, as the cross-sectional area is a key factor in determining resistance. By increasing the area through parallel connections, the resistance is reduced, allowing more current to flow through the circuit.

As seen by the equation [math]\displaystyle{ R = \frac{\rho L}{A} }[/math], doubling the Area would cut the resistance in half and effectively double the conductance of the circuit containing the conductors seeing that [math]\displaystyle{ \sigma = \frac{1}{\rho} }[/math]

In the realm of electrical engineering, a standard wire exemplifies a practical application of Ohm's Law. This fundamental law delineates the correlation between the flow of electric charge and the electric field responsible for this flow. Ohm's Law is articulated through two essential equations:

The first equation explicitly states the relationship:

[math]\displaystyle{ \vec{J} = \sigma \vec{E} }[/math]

Here, [math]\displaystyle{ \vec{J} }[/math] represents the current density, and [math]\displaystyle{ \vec{E} }[/math] signifies the electric field. The concept of current density refers to the amount of charge traversing a specified cross-sectional area within a certain time frame, measured in SI units as [math]\displaystyle{ \frac{A}{m^2} = \frac{C}{m^2 \cdot s} }[/math]. This elucidates that current density is a 'density' with 'area' in its denominator.

Another aspect related to Ohm's Law is the "skin effect," which elucidates the interplay between current density and the radius of a wire. It posits that a larger wire radius leads to increased current density. This effect is integral to understanding Ohm's Law in practical scenarios.

Another commonly used form of Ohm's Law is expressed as:

[math]\displaystyle{ V = I R }[/math]

Where [math]\displaystyle{ V }[/math] is the electric potential, [math]\displaystyle{ I }[/math] the current, and [math]\displaystyle{ R }[/math] the resistance. This version of the law is widely employed in various electrical engineering applications.

Computational Method

This topic is largely conceptual and algebraic, so there is relatively little modeling to be done. However, this program is designed to create plots of the relationship between resistance, resistivity, length and cross sectional area.

Code shows the relationship between:

Resistance and length across different fixed points

Resistance and area across different fixed points

Furthermore, this external program provides a good visual demonstration of the relationship that acts as a good simulation for altering either the volume, conductance, current, or area of an object to see how the resistance will be altered (but unfortunately the source code is not accessible).

Examples

Simple

Example Number 1

A semi conductive material has a resistivity of [math]\displaystyle{ 200 \; \Omega\cdot m }[/math]. What is its conductivity?

Solution

Since conductivity is the reciprocal of resistivity,

[math]\displaystyle{ \sigma = \frac{1}{\rho} = \frac{1}{200 \; \Omega \cdot m} = 0.005 \frac{1}{\Omega \cdot m} }[/math]

Example Number 1.2

A copper wire has a resistivity of [math]\displaystyle{ 1.68 \times 10^{-8} \; \Omega\cdot m }[/math] at room temperature. Determine its conductivity.

Solution

Given that conductivity is the inverse of resistivity,

[math]\displaystyle{ \sigma = \frac{1}{\rho} = \frac{1}{1.68 \times 10^{-8} \; \Omega \cdot m} = 5.95 \times 10^{7} \frac{1}{\Omega \cdot m} }[/math]

This result indicates high conductivity, characteristic of copper.

Example Number 1.3

Calculate the resistivity of an aluminum material with a conductivity of [math]\displaystyle{ 3.5 \times 10^{7} \frac{1}{\Omega \cdot m} }[/math].

Solution

Since resistivity is the reciprocal of conductivity,

[math]\displaystyle{ \rho = \frac{1}{\sigma} = \frac{1}{3.5 \times 10^{7} \frac{1}{\Omega \cdot m}} = 2.86 \times 10^{-8} \; \Omega\cdot m }[/math]

This value of resistivity is typical for aluminum.

Example Number 2

An unknown material is used in the creation of a video game console.

Part A: How would the amount of free electrons in the material affect the conductance of the material?

Part B: Would the material's conductance increase or decrease if you put the material in the freezer as opposed to room temperature?

Solution For Part A

The conductance of a material is directly influenced by the number of free electrons available for conduction. A higher number of free electrons implies lower resistance, as conductance is inversely related to resistivity ([math]\displaystyle{ \sigma = \frac{1}{\rho} }[/math]). Therefore, an increase in free electrons results in higher conductance.

Solution For Part B

Lowering the temperature of a material typically increases its resistivity, as free electron movement is slowed. This results in a decrease in conductance. In colder environments (like a freezer), the slowed electron movement leads to increased resistance and consequently, decreased conductance in the material.

Middling

Example Number 1

An electric potential of [math]\displaystyle{ 120 V }[/math] is applied to a circular wire of length [math]\displaystyle{ 2 \cdot 10^4 \; m }[/math] and radius [math]\displaystyle{ 0.001 m }[/math]. The current is equal to [math]\displaystyle{ 1.11 \; A }[/math]. Determine the resistivity, and match it to an elemental metal using an appropriate table (such as ^[6])

Solution

We have Ohm's Law

[math]\displaystyle{ V = I R }[/math]

and so plugging in our definition for resistance in terms of resistivity gives that

[math]\displaystyle{ V = \frac{I \rho L}{A} }[/math]

which we rearrange to get

[math]\displaystyle{ \rho = \frac{ V A}{I L} }[/math]

plugging all of the values in gives an answer of [math]\displaystyle{ \rho = 1.7 \cdot 10^{-8} \; \Omega \cdot m }[/math], which is the resistivity of copper.

Example Number 2

A student wishes to cut a wire in order to reach a specific potential difference.

Given what we know about Ohm's law, a student discovers that the wire she is using in a circuit to light a light bulb has a resistance of [math]\displaystyle{ \rho = 2.0 \cdot 10^{-7} \; \Omega \cdot m }[/math] and a radius of .002 meters. The current in the circuit is equal to 1 Amepere. The student then realizes that in order for the light bulb to be lit, there must be an electric potential across the light bulb of at least 100 Volts. Given that there are no other resistors in the circuit, determine the necessary length of the wire that she would need to cut in order for the potential difference of the wire to equal 100 Volts.

Solution

We can start by rearranging Ohm's Law

Ohms Law is equal to

[math]\displaystyle{ V = I R }[/math]

and so plugging in our definition for resistance in terms of resistivity gives that

[math]\displaystyle{ V = \frac{I \rho L}{A} }[/math]

which we rearrange to get

[math]\displaystyle{ \rho = \frac{ V A}{I L} }[/math] like in example 1

If the equation is even more rearranged in order to find the necessary length she needs to cut of the wire to get a potential difference, the equation would be

[math]\displaystyle{ L= \frac{ V* A}{I*rho} }[/math]

The next step is to use the radius of the wire in the given problem to find the area

Area= pi*r^2

If you plug in the numbers you get [math]\displaystyle{ L=100*(pi*(.002)^2)/(2.0 \cdot 10^{-7}*1) }[/math]

This gives you a necessary length of 6.28 \cdot 10^{5} meters

Difficult

One cubic meter of a fictional material with resistivity [math]\displaystyle{ \rho = 10^{-5} \; \Omega \cdot m }[/math] is formed into a shape with uniform cross sectional area (such that volume is equal to the base times the height) for which the resistance to current run lengthwise is equal to [math]\displaystyle{ 10 \; \Omega }[/math]. Determine the dimensions (length and cross sectional area) of the shape, presuming that it follows Ohm's law and the equation for resistance given above.

Solution

As the clarification hints, it is necessary to use a little basic geometry to solve this problem, namely

[math]\displaystyle{ V = L \cdot A }[/math]

So we lay out the standard formula

[math]\displaystyle{ R = \frac{\rho L}{A} }[/math]

Then multiply both numerator and denominator by [math]\displaystyle{ L }[/math] to obtain

[math]\displaystyle{ R = \frac{\rho L^2}{A L} = \frac{\rho L^2}{V} }[/math]

From here it is simply rearrangement to find that

[math]\displaystyle{ L = \sqrt{\frac{R V}{\rho}} = \sqrt{\frac{(1 \;m^3)(10 \;\Omega)}{10^{-5} \; \Omega \cdot m }} = 10^2 \; m }[/math]

With the length determined, it is then straightforward to conclude that [math]\displaystyle{ A = 10^{-2} \; m^2 }[/math], and the cross-section can take any shape which has that enclosed area.

Connectedness

Every time an electrical system has been created, an understanding of conductivity and resistivity had to be determined.

Since conductivity and resistivity are related, it is reasonable to assume that wires or components with low electric resistivity make good conductors due to their ability to effectively transmit electricity and heat. Conversely, materials with high electric resistivity are less efficient at conducting and are often used as insulators.

This concept has significant applications in real life, including:

Home insulation: Utilizing materials with high resistivity to maintain indoor temperature.
Cooking: Employing pots, pans, and other metallic objects with low resistivity for efficient heat transfer, allowing food to cook evenly without direct exposure to the stove's heat source.
Electronic Devices: Using materials with high resistivity in electronic devices to regulate temperature and prevent overheating, caused by the constant flow of electrical current.

Measuring Conductivity

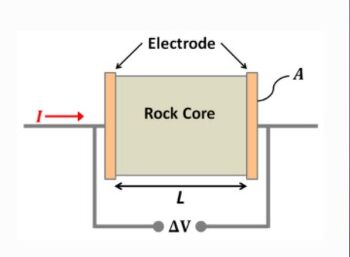
To measure conductivity^[7], a sample of the material is placed in between two metallic electrodes, either made of copper or granite. Ohm's law is then used to calculate the numerical value of the resistance of the circuit.

^[8]

This is done through monitoring the current that is produced from the loop and the [math]\displaystyle{ delta V }[/math] that can be measured through the attachment of an ammeter to the copper or granite circuit. The stronger conductors would have a higher <health>delta V<delta V> value and/or a lower I, a larger convection current.

History

The study of conductivity and resistivity has a rich history, marked by significant contributions from various scientists. One of the earliest contributors was Stephen Gray, who along with Ganvil Wheler, observed that electricity could be transmitted over distances and that different materials had varying effectiveness in conducting electricity. This early observation, contrasting the conductivity between silk and brass wires, laid the groundwork for future studies [9].

While the 18th century saw notable advancements in understanding electricity, including the work of Benjamin Franklin, these developments were more closely tied to broader aspects of electrical science rather than specifically to conductivity and resistivity.

The early 19th century marked a pivotal moment in the study of resistivity and conductivity. Antoine Becquerel, the grandfather of Henri Becquerel who later became renowned for his work in radioactivity alongside Marie Skłodowska Curie and Pierre Curie, formulated an equation to determine resistance from resistivity and geometry [10]. This breakthrough provided a more quantitative approach to understanding how electrical resistance was influenced by material properties and structural dimensions.

Following Becquerel's work, Georg Ohm, a German physicist, proposed a theorem relating current, potential, and resistance. Although his initial proposition was incorrect, he soon revised it, leading to the formulation of Ohm's law. Despite initial skepticism and poor reception due to philosophical differences and confusion over the definitions of resistance, current, and potential, Ohm's work eventually gained acceptance and recognition, transforming our understanding of electrical resistance and its relationship to current and voltage.

This period marked a crucial era in the study of electrical properties, as scientists began to establish the fundamental principles that would shape our modern understanding of electrical conductivity and resistivity.

[5] ttps://home.cern/science/engineering/superconductivity

[6] ttp://hyperphysics.phy-astr.gsu.edu/hbase/Tables/elecon.html

[7] ttps://gpg.geosci.xyz/content/physical_properties/physical_properties_conductivity.html

[8] ttps://gpg.geosci.xyz/content/physical_properties/induced_polarization_physical_properties_duplicate.html

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Conductivity and Resistivity

Contents

Main Idea

Mathematical Method

Computational Method

Examples

Simple

Middling

Difficult

Connectedness

History

See Also

Further reading

External links

References

Navigation menu