Collisions

Claimed by mdumenci3 for Fall 2017. SECOND EDIT BY SUNGJAE HYUN IN 2016-04-16 ADDITIONS MADE BY Sam Webster 4-17-16

This topic covers Collisions, a comprehensive way to combine the Momentum and Energy Principles.

The Main Idea

Collisions are special types of contact interactions between objects. From a physics standpoint, collisions are a way to combine the Momentum and Energy Principles. In the case of collisions, if we choose a system of the two objects interacting, the change in momentum of the system and the change in energy of the system are both zero. With this in mind, calculations with collisions become very simple. We are able to choose a system of only the two objects (excluding external forces such as the Earth's gravity) because the collision takes place during such a short time that the external forces have a negligible effect. There are two types of collisions, Elastic Collisions and Inelastic Collisions.

A Mathematical Model

[math]\displaystyle{ {E}_{f} = {E}_{i} }[/math] where [math]\displaystyle{ {E}_{f} }[/math] is the total final energy of the system and [math]\displaystyle{ {E}_{i} }[/math] is the total initial energy of the system.

[math]\displaystyle{ {p}_{f} = {p}_{i} }[/math] where [math]\displaystyle{ {p}_{f} }[/math] is the total final momentum of the system and [math]\displaystyle{ {p}_{i} }[/math] is the total initial momentum of the system. (ie. [math]\displaystyle{ m_{f_1}v_{f_1} + m_{f_2}v_{f_2} + ... + m_{f_n}v_{f_n} = m_{i_1}v_{i_1} + m_{i_2}v_{i_2} + ... + m_{i_n}v_{i_n} }[/math])

A Computational Model

The following situation was used for this model created using python:

Two objects are initially moving towards a third stationary object. Object 1 (in red) at position (-10,0,-2)m has a mass of 2kg and velocity (10,0,2)m/s. Object 2 (in blue) at position (0,6,3)m has a mass of 4kg and velocity (0,-6,3)m/s. Object 3 (in orange) at the origin has a mass of 5kg. The objects collide at the origin and after the collision it is observed that object 1 has embedded in object 3 (hence it is no longer visible in the model) and the combined object moves with velocity (5,-6,0)m/s (This is an example of a Maximally Inelastic Collision). The final velocity of object 2 is calculated and used in the rest of the simulation. (NOTE: the white sphere visible after the collision represents the origin to add dimension to the model and the delay during the collision is there to emphasis when and where the collision happens. Also use the link below the model for a more detailed explanation of the calculations and concepts.).

Check out the code used for the simulation at [1]. The code is commented pretty heavily (but it does assume some knowledge of python and python animations) in hopes that future students can modify some of the variables to experiment with creating different results.

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Example 1) A 0.5 kg soccer ball is moving with a speed of 5 m/s directly toward to 0.7 kg basket ball which is at rest. When two balls collide and stick together what will their final velocity be?

Before Collision: 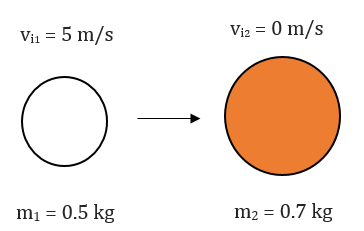After Collision:

___

Variables:

[math]\displaystyle{ m_1 = 0.5 }[/math] [math]\displaystyle{ kg }[/math]

[math]\displaystyle{ v_{i_1} = 5 }[/math] [math]\displaystyle{ m/s }[/math]

[math]\displaystyle{ m_2 = 0.7 }[/math] [math]\displaystyle{ kg }[/math]

[math]\displaystyle{ v_{i_2} = 0 }[/math] [math]\displaystyle{ m/s }[/math]

[math]\displaystyle{ v_f = ? }[/math]

So, [math]\displaystyle{ m_1v_{i_1} + m_2v_{i_1} = (m_1 + m_2)v_f }[/math]

[math]\displaystyle{ LHS = (0.5 }[/math] [math]\displaystyle{ kg) }[/math][math]\displaystyle{ (5 }[/math] [math]\displaystyle{ m/s) + }[/math] [math]\displaystyle{ (0.7 }[/math] [math]\displaystyle{ kg) }[/math][math]\displaystyle{ (0 }[/math] [math]\displaystyle{ m/s) = }[/math] [math]\displaystyle{ 2.5 }[/math] [math]\displaystyle{ kg*m/s }[/math]

[math]\displaystyle{ RHS = (0.5 }[/math] [math]\displaystyle{ kg + }[/math] [math]\displaystyle{ 0.7 }[/math] [math]\displaystyle{ kg) }[/math][math]\displaystyle{ (v_f) = }[/math] [math]\displaystyle{ (1.2 }[/math] [math]\displaystyle{ kg) }[/math][math]\displaystyle{ (v_f) }[/math]

[math]\displaystyle{ LHS = RHS }[/math] in an inelastic collision

[math]\displaystyle{ 2.5 }[/math] [math]\displaystyle{ kg*m/s = }[/math] [math]\displaystyle{ (1.2 }[/math] [math]\displaystyle{ kg) }[/math][math]\displaystyle{ (v_f) }[/math]

[math]\displaystyle{ v_f = }[/math] [math]\displaystyle{ (2.5 }[/math] [math]\displaystyle{ kg*m/s) }[/math] [math]\displaystyle{ / }[/math] [math]\displaystyle{ (1.2 }[/math] [math]\displaystyle{ kg) = }[/math] [math]\displaystyle{ 2.08333 }[/math] [math]\displaystyle{ m/s }[/math]

Thus, the final velocity is 2.08 m/s. Since the two balls stick together, this is an example of a Maximally Inelastic Collision.

Middling

Example 2) A bullet of 50 caliber machine gun is 42 grams. It strikes a wooden target block of mass 10 kg stationed on a friction-less surface. The wooden block gains velocity of 1.8 m/s after being embedded with the bullet. What was the velocity of the bullet before it collided with the target?

Before Collision: 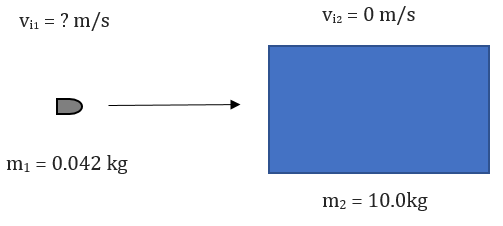After Collision: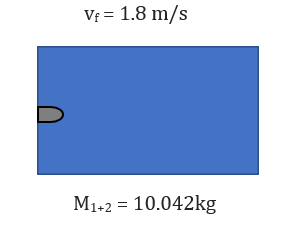

Variables:

[math]\displaystyle{ m_1 = 42 }[/math] [math]\displaystyle{ g }[/math] [math]\displaystyle{ / }[/math] [math]\displaystyle{ 1000 }[/math] [math]\displaystyle{ g = }[/math][math]\displaystyle{ 0.042 }[/math] [math]\displaystyle{ kg }[/math]

[math]\displaystyle{ v_{i_1} = ? }[/math]

[math]\displaystyle{ m_2 = }[/math] [math]\displaystyle{ 10 }[/math] [math]\displaystyle{ kg }[/math]

[math]\displaystyle{ v_{i_2} = }[/math] [math]\displaystyle{ 0 }[/math] [math]\displaystyle{ m/s }[/math]

[math]\displaystyle{ m_{1+2} = (m_1+m_2) = 0.042 }[/math] [math]\displaystyle{ kg + }[/math] [math]\displaystyle{ 10.0 }[/math] [math]\displaystyle{ kg = }[/math] [math]\displaystyle{ 10.042 }[/math] [math]\displaystyle{ kg }[/math]

[math]\displaystyle{ v_f = }[/math] [math]\displaystyle{ 1.8 }[/math] [math]\displaystyle{ m/s }[/math]

[math]\displaystyle{ (m_1)(v_{i_1}) + (m_2)(v_{i_2}) = (m_{1+2})(v_f) }[/math]

[math]\displaystyle{ (0.042 }[/math] [math]\displaystyle{ kg)(v_{i_1}) = }[/math] [math]\displaystyle{ (10.042 }[/math] [math]\displaystyle{ kg)(1.8 }[/math] [math]\displaystyle{ m/s) }[/math]

[math]\displaystyle{ v_{i_1} = (18.0756 }[/math] [math]\displaystyle{ kg*m/s) }[/math] [math]\displaystyle{ / }[/math] [math]\displaystyle{ (0.042 }[/math] [math]\displaystyle{ kg) = }[/math] [math]\displaystyle{ 430.37 }[/math] [math]\displaystyle{ m/s }[/math]

Final Answer: The bullet's initial speed is 430.37 m/s.

Difficult

Example 3) Two rocks in space are approaching a third stationary rock. Rock 1 has mass 30kg moves with velocity (13,-10,-2)m/s. Rock 2 has mass 60kg and moves with velocity (-3,23,3)m/s. Rock 3 has mass 35kg and is stationary. The rocks collide at rock 3's location. After the collision it is observed that Rock 1 has embedded into Rock 3, but a chunk of mass 15kg has broken off of the combined rock, Rock 3'. It is also noticed that Rock 2 is now moving with velocity (-2,12,2)m/s. (NOTE: due to the difficulty and use of three dimensions it is suggested to use a computer to solve this problem. Therefore the sample solution will involve code, but conceptually everything remains the same. Additionally some code is omitted for the sake of saving space, but the important calculations are included. See the entire code at [2] with a model of the collision )

First determine the momentum of Rock 3' plus the momentum of the 15kg chunk.

Having defined the rocks as o1, o2, and o3 respectively, and defined there initial masses and velocities to calculate their individual momenta

calculated the total momentum of the system by adding

totalP = o1.p+o2.p+o3.p #total momentum of the system

Next update the o1, o2 and o3 objects with the information observed after the collosions

mChunk = 15 # in kg

m1f = 0 #final mass object 1 in kg

m2f = 60 #final mass object 2 in kg

v2f = vector(-2,12,2) #final elocity object 2 in m/s

m3f = o1.m + o2.m - mChunk #final mass object 3 in kg

create a new sphere object with mass 15kg (code omitted)

calculate the final momentum of rock 2

o2.p = o2.v*o2.m

finally determine the combined momentum of rock 3' and the chunk using the momentum principle

pOfRock3PrimeAndChunk = totalP - o2.p #for now we are only calculating the combined momentum of rock 3' and the chunk

The combined momentum of Rock 3' and the Chunk is <330, 360, 0>kg*m/s

Later Rock 3' is observed moving with velocity (3,5,2)m/s, what is the velocity of the 15kg chunk?

Now we know the momentum of Rock 3' plus the chunk, AND we know the velocity and mass of Rock 3'

pRock3Prime = m3f*vector(3,5,2) #calculate the momentum of Rock3'

pChunk = pOfRock3PrimeAndChunk - pRock3Prime #calculate the momentum of the chunk

chunk.v = pChunk/chunk.m #calculate the final velocity of the chunk

The velocity of the chunk is <7, -1, -10>

With the information you know, determine the combined change in internal energy for all of the rocks.

Start by calculating the total Kinetic Energy initial and the total Kinetic Energy final (In the actual program this has to go above the update statements for after the collision)

o1.K = .5*o1.m*o1.v**2

o2.K= .5*oK.m*o1.v**2

o3.K = 0 #because it is stationary

kTotInitial = o1.K+o2.K

Now after the collision (in the actual program these go after the update statements for after the collision)

o2.K = .5*o2.m*o2.v**2

kRock3Prime = .5*m3f*mag(vector(3,5,2))**2

chunk.K = .5*chunk.m*chunk.v**2

kTotFinal = o2.K + kRock3Prime + chunk.K

Now since there aren't any outside forces doing work and contributing energy, we know that change in internal energy equals -1*change in Kinetic energy, or kTotInitial - kTotFinal

changeInInternalEnergy = kTotInitial - kTotFinal

The change in internal energy is 5175J

Connectedness

Collisions are interesting phenomenons that are applicable to everyday situations. Some examples are when a bat collides with a baseball in your neighbor's backyard, two cars crashing in the highway in front of you, and two linebackers running into each-other at your local College's spring football game. Depending on the type of collision, you can predict if there will be a change in internal energy (thermal energy, chemical energy etc.). Another very interesting application of collisions is in the field of astronomy. The universe is ever-changing and we never know what might come our way. A large meteor could be flying at the Earth with a very high speed and we could use our knowledge of collisions to find out how the Earth will move after the collision, what the temperature change of the area would be, and how the rest of the Earth would be effected by the collision. By using our collision skills, we could evacuate anyone who is prone to harm during the collision.

Knowledge of collisions is also a must for many engineering majors. Industrial engineers must take in collisions when they are trying to optimize complex systems. For instance, an Industrial engineer must make sure that the bridge he or she builds can withstand the forces the cars can exert on it. Architects and Civil engineers must design houses in a certain way so that slight collisions with other objects won't completely knock the house down. And of course, Mechanical engineers and Aerospace engineers must take into account collisions when designing and maintaining mechanical systems.

History

In 1661, Christiaan Huygens, a Dutch physicist, concluded that when a moving body struck a stationary object of equal mass, the initial moving body would lose all of its momentum while the second object would pick up the same amount of velocity that the moving body had before the collision. He also stated that the total "quantity of motion" should be the same before and after the collision. This was the first thought of the conservation of momentum.

In 1687, Sir Isaac Newtons went a little further and stated in his third law of motion that the forces of action and reaction between two bodies are opposite and equal.

In Rutherford's Gold Foil Experiment in 1899, Rutherford found out that the plum pudding model of the atom was inaccurate and that there was actually a massive center of atoms. He did this through investigating atomic collisions between atoms and gold foil. Because some particles were scattered through angles larger than 90 degrees during the collisions, he was able to conclude that the atom had most of it's mass concentrated in a dense center rather than spread out evenly throughout the atom.

Collisions

Contents

The Main Idea

A Mathematical Model

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu