Inertia

Claimed by Dev Mandavia

The property of matter by which it continues in its existing state of rest or uniform motion in a straight line unless acted on by an external force. Sometimes referred to as momentum, inertia is a property of matter that allows for scientists to describe how motion is changed by forces. It is the natural tendency of objects to remain in motion or to remain at rest.

The Main Idea

Newton challenged past assertions regarding laws of motion with his concept that objects in motion tend to stay in motion unless acted on by an external force. This is antithetical to the prior thought that objects naturally come to a state of rest.

History

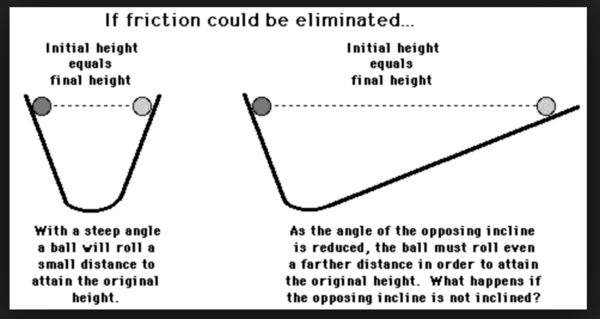
Galileo performed an experiment with two ramps and a bronze ball. To begin, the two were set up at the same angle. Galileo observed that if a ball was released at one height, it would roll to the same height at which the ball was released. He then experimented with altering the angle of the second ramp. He concluded that even though it may take longer, when the angle is smaller, the ball will still roll up to the same height. Because the height was conserved, Galileo believed that if a ball was rolled from a ramp to a flat surface, it would stay in motion unless a force stopped it, such as friction.

Calculating Inertia

Momentum is conserved by

[math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net}{Δt} }[/math]

and calculated by

[math]\displaystyle{ \vec{p} = m*\vec{v} }[/math]

when in non-curving motion.

Otherwise, the inertia is then moment of inertia. The formula for moment of inertia depends on what the particular object is as well as its rotational axis.

Examples

Basic Inertia

Inertia, or momentum, of an object is calculated by multiplying the velocity by the mass.

For example, a car that weighs 3000 kilograms is moving at a velocity of 26 meters per second. What is the inertia of the car?

To solve this, one must use [math]\displaystyle{ \vec{p} = m*\vec{v} }[/math]

m = 3000kg and v = 26[math]\displaystyle{ {\frac{m}{s}} }[/math]

[math]\displaystyle{ \vec{p} = 3000*26 = 78000 Ns }[/math]

Moment of Inertia

A disc of mass 1 kg is rotating and has a radius of .1 meter. What is the moment of inertia of the disc?

The formula for the moment of inertia of a disc is [math]\displaystyle{ {\frac{1}{2}}mr^2 }[/math]

m = 1 kg and r = .1 m

[math]\displaystyle{ {\frac{1}{2}}(1)*(.1)^2 = 0.005 kg*m^2 }[/math]

Relationship to Modern Day Life

Anything in life involving motion is inertia, whether it is you walking, riding a scooter, or running. A ball's motion or lack of motion is inertia as well. An everyday example of inertia would be a car in motion. As a car accelerates and attains a higher velocity, the amount of momentum of the vehicle increases. A higher inertia makes it more difficult for a car to brake quickly and come to a halt in an emergency scenario.

References

[[1]] [[2]] [[3]]