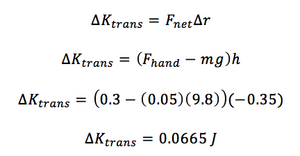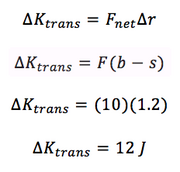Point Particle Systems

This page describes point particle systems and how they can be used to model certain aspects of a system's motion.

The Main Idea

A point particle system is a physical system, usually composed of multiple parts, modeled as though it were a single particle at its center of mass.

When work is done on a system, the energy imparted on it may take on multiple forms. These include Translational, Rotational and Vibrational Energy, Potential Energy, and Thermal Energy. Translational kinetic energy is kinetic energy due to the movement of the system's center of mass. All other types of energy the system has are considered "internal" types of energy because they do not affect the system's motion through its environment, but rather indicate its local properties. Sometimes, when work is done on a system, it imparts both translational kinetic energy and internal types of energy. For example, consider a ball rolling down a ramp. Gravity does work on the ball and increases its energy. It gains some translational kinetic energy (its center of mass gains a velocity down the ramp) and some rotational kinetic energy (its rolling motion causes it to rotate about its center of mass).

The purpose of modeling a system as a point particle system is to isolate the work done on it that raises its translational kinetic energy, which may only be a fraction of the total work done on the system. This is because point particles cannot have any internal types of energy. Modeling a system as a point particle system can make it much easier to calculate its motion through its environment, but offers no insights about the internal state of the system.

Point particle systems are in contrast to Real Systems (also known as extended systems), which analyze each part of a system individually instead of reducing it to a single point. Real systems can model a system's internal behavior in addition to its motion through its environment, although they can be very complicated and difficult to analyze quantitatively. Often, to obtain a complete model of a system's behavior, both point-particle and extended models are used.

A Mathematical Model

For a point particle system, the work-energy theorem is still true (see Work/Energy).

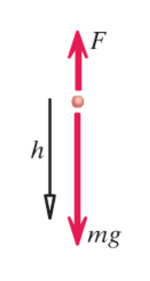
The work done on a point particle system is defined as

[math]\displaystyle{ W = \int \vec{F_{net}} \cdot d \vec{r} }[/math].

Let us assume that the net force acting on the particle is constant, so that we can get rid of the integral, and that the net force acts in the direction of the particle's motion, so that we can replace the dot product with regular multiplication. This will be the case for most point particle system problems. With these assumptions, the work done on a point particle is given by

[math]\displaystyle{ W = F_{net} d }[/math]

where [math]\displaystyle{ F_{net} }[/math] is the magnitude of the net force acting on the particle and [math]\displaystyle{ d }[/math] is the distance traveled by the particle.

The work-energy theorem states that work done on a system increases that system's energy. A point particle cannot experience an increase in internal energy. For example, the moment of inertia of a point particle about its center of mass is 0, so it can have no rotational kinetic energy. This means that all of the work done on a point particle system becomes translational kinetic energy.

In other words, for a point particle system,

[math]\displaystyle{ \Delta KE = F_{net} d }[/math]

and

[math]\displaystyle{ KE = \frac{1}{2} m v^2 }[/math].

The two equations above are the basis for answering questions using point particle systems.

Examples

Jumper Model

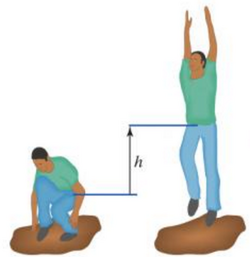
A person jumps straight up in the air from a crouching position. Their center of mass moves h, or 2 m. Their total mass, m is equal to 60 kg. Find the velocity of the center of mass of the jumper. When the jumper jumps, the normal force of the ground is equal to 2x the force of gravity.

To make this problem simpler, use the center of mass of the person to collapse the whole system to one point.

Imagine the jumper's center of mass as a point, and it moves up 2 m.

Remember, , and . We need to find Fnet. The only forces acting on the jumper are the gravitational force of the Earth and the normal force. Therefore,

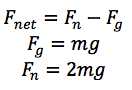
Steps:

Notice that the initial translational kinetic energy is 0, as the person is initially at rest. When worked out, the v = 6.26 m/s.

The final translational kinetic energy can be used for further calculations if one was to calculate the total change in energy of the real system. These calculations would allow you to find the change in various forms of internal energy, such as heat energy or chemical energy.

---

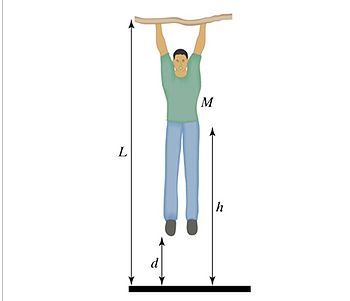
Another example that the point particle system can be applied to is someone hanging motion-less and then jumping down into a crouch position.

Looking at the system as a point particle system, you can look at the initial and final states of the man in order to find the change in energy. We are going to again use a formula for work,

In order to find the speed just before your feet touch the ground, you can set an equation as the following:

The equation for the point particle system ∆E= ∆K=Work can be applied in order to find different variables asked for in a problem.

Remember that if the man does not move, then the work done by the man will be 0 joules, because there is no displacement.

Yo-Yo Example

You pull up on a string the distance d, 0.2 m, with a force, F, 0.3 N. The yo-yo falls a distance h, 0.35 m. The mass of the yo-yo, m, is 0.05 kg. What is the change in translational kinetic energy?

For this example, the Fnet is equal to the force of your hand and the gravitational force of the earth. Delta r is equal to the movement of the yo-yo down, h.

Steps:

This information could be used to solve for the extended system, which would include the work done by your hand and the earth, as well as rotational kinetic energy.

Spring in a Box Example

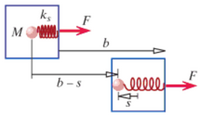
Suppose a thin box contains a ball of clay with the mass M, 2 kg, connected to a relaxed spring, with a stiffness ks, 1.2. The masses of the box and the spring are negligible. It is initally at rest, and then a constant force of F, or 10 N. The box moves a distance b, 1.5 m, and the spring stretches a distance s, 0.3 m, so that the clay sticks to the box. What is the translational kinetic energy of the box?

For the point particle system, the center of mass is the clay because the other masses are negligible. Therefore, delta r is equal to b-s, or 1.2 m. The only force acting on is F in the +x direction.

Steps:

This information could then be used for the extended system. In this example, the extended system would also include the work done by the force F, the potential energy of the spring,as well as any other internal energies.

Connectedness

1. How is this topic connected to something that you are interested in?

I find the entire realm of physics fascinating, and I find it interesting how physicists are constantly coming up with new ways to solve problems and use formulas. The point particle system is a perfect example of that. It can turn a complicated force problem into something easy to approve. I also find it interesting how you can find other forms of energy, such as chemical energy, by using point particle and real systems. Something so small and seemingly unattainable can be found using this method.

1. How is it connected to your major?

I am majoring in Materials Science and Engineering, and there are many ways all different types of physics can be used in MSE. The engineering of materials, specifically being able to calculate the amount and types of energy (and thus the cost) to produce something is absolutely crucial. Point particle systems can make this easier to do, while also adding precision to the calculations.

1. An interesting industrial application

As seen in the above examples, there are many real life applications to point particle systems, such as the energy in a person falling, or in a yoyo. This system can also be applied to industry and manufacturing, with the use of various machines that may require gears, levers, or other objects that rotate. Using point particle and real systems, you can calculate the amount of internal energy happening in a moving machine, and therefore how much energy is lost.

See also

Further reading

For more help, a helpful page is: http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:pp_vs_real

A helpful video lecture: https://www.youtube.com/watch?v=T780lL5FlLg&index=41&list=PL9HgJKLOnKxedh-yIp7FDzUTwZeTeoR-Y

External links

See also Real Systems for further information on using Point Particle Systems to solve for the Real Systems.

References

Chabay, Ruth W., and Bruce A. Sherwood. "9." Matter & Interactions. N.p.: n.p., n.d. N. pag. Print.

Purdue Physics. https://www.physics.purdue.edu/webapps/index.php/course_document/index/phys172/1160/42/5399.

Yo-yo Clipart: https://www.clipartbest.com