Spring Motion: Difference between revisions
No edit summary |
No edit summary |
||
| Line 5: | Line 5: | ||
==Spring Motion== | ==Spring Motion== | ||
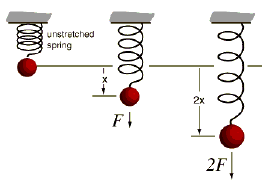
Spring motion is often used to describe the motion of a mass attached to | Spring motion is often used to describe the motion of a mass attached to a spring. Unlike what you may have encountered before, the net force acting on the mass is not constant, but is based on the amount that a spring is stretched or compressed. Every spring has it's own natural resting point, referred to as <math> L_0 </math> mathematically, which represents the length of the spring should the spring-mass system be at rest. When the length of the spring equals <math> L_0 </math>, the force it would apply to an attached mass is zero. Although often referred to in a one dimensional setting, where all Force, Velocity, and Displacement are among one axis, Spring Motion and its related formulas can be used to describe both two and three dimensional movement as well. | ||
If the length of the spring is changed from <math> L_0 </math>, it results in a restorative force that attempts to restore the length of the spring to <math> L_0 </math>. Compressing the spring to make its length less than <math> L_0 </math> causes the spring to want to expand, pushing any attached object outward, and stretching the spring to make its length greater than <math> L_0 </math> results in a force pulling any attached object inward. Compressing the spring to make its length less than <math> L_0 </math> causes the spring to want to expand, pushing any attached object outward, and stretching the spring to make its length greater than <math> L_0 </math> results in a force pulling any attached object inward. Newton's First Law states that <math> F = ma </math>, which means that the direction of the Force is the same as the direction of acceleration of the mass, meaning that the acceleration of the spring is always in the direction of <math> L_0 </math>. | |||
When a mass is permanently attached to a mass, the mass' velocity increases as it approaches <math> L_0 </math> and decreases the further away it gets, causing an oscillation. In some cases, this may result in *[[Simple Harmonic Motion]] | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
We can find the force that the spring is exerting on a mass using the formula: <math> F_{spring} = -k_s*s*L_{hat} </math> | We can find the force that the spring is exerting on a mass using the formula: <math> F_{spring} = -k_s*s*L_{hat} </math>, where <math> k_s </math> is the specific stiffness of the spring (how hard it is to stretch / compress), <math> s </math> is the difference in length of the spring from its current to relaxed length, found using the following equation <math> s= L - L_0 </math>, and <math> L_{hat} </math> is the unit vector indicating the direction of the vector pointing from the spring's origin to the mass - essentially which direction the Force is pointing. | ||
where <math> k_s </math> is the specific stiffness of the spring (how hard it is to stretch / compress), <math> s </math> is the | |||
Spring motion can be predicted using the momentum principle <math> dp=F_{net}*dt </math> and the position-update formula <math> dr= p_f/m*dt </math> Because spring motion involves oscillation, it is important to iterate with a small enough change in time to capture the full path of the spring-mass system. | Spring motion can be predicted using the momentum principle <math> dp=F_{net}*dt </math> and the position-update formula <math> dr= p_f/m*dt </math> Because spring motion involves oscillation, it is important to iterate with a small enough change in time to capture the full path of the spring-mass system. | ||
Revision as of 17:25, 2 December 2025
by Caroline Ware
Claimed to edit by Adam Green, Fall 2025
Spring Motion
Spring motion is often used to describe the motion of a mass attached to a spring. Unlike what you may have encountered before, the net force acting on the mass is not constant, but is based on the amount that a spring is stretched or compressed. Every spring has it's own natural resting point, referred to as [math]\displaystyle{ L_0 }[/math] mathematically, which represents the length of the spring should the spring-mass system be at rest. When the length of the spring equals [math]\displaystyle{ L_0 }[/math], the force it would apply to an attached mass is zero. Although often referred to in a one dimensional setting, where all Force, Velocity, and Displacement are among one axis, Spring Motion and its related formulas can be used to describe both two and three dimensional movement as well.
If the length of the spring is changed from [math]\displaystyle{ L_0 }[/math], it results in a restorative force that attempts to restore the length of the spring to [math]\displaystyle{ L_0 }[/math]. Compressing the spring to make its length less than [math]\displaystyle{ L_0 }[/math] causes the spring to want to expand, pushing any attached object outward, and stretching the spring to make its length greater than [math]\displaystyle{ L_0 }[/math] results in a force pulling any attached object inward. Compressing the spring to make its length less than [math]\displaystyle{ L_0 }[/math] causes the spring to want to expand, pushing any attached object outward, and stretching the spring to make its length greater than [math]\displaystyle{ L_0 }[/math] results in a force pulling any attached object inward. Newton's First Law states that [math]\displaystyle{ F = ma }[/math], which means that the direction of the Force is the same as the direction of acceleration of the mass, meaning that the acceleration of the spring is always in the direction of [math]\displaystyle{ L_0 }[/math].
When a mass is permanently attached to a mass, the mass' velocity increases as it approaches [math]\displaystyle{ L_0 }[/math] and decreases the further away it gets, causing an oscillation. In some cases, this may result in *Simple Harmonic Motion
A Mathematical Model
We can find the force that the spring is exerting on a mass using the formula: [math]\displaystyle{ F_{spring} = -k_s*s*L_{hat} }[/math], where [math]\displaystyle{ k_s }[/math] is the specific stiffness of the spring (how hard it is to stretch / compress), [math]\displaystyle{ s }[/math] is the difference in length of the spring from its current to relaxed length, found using the following equation [math]\displaystyle{ s= L - L_0 }[/math], and [math]\displaystyle{ L_{hat} }[/math] is the unit vector indicating the direction of the vector pointing from the spring's origin to the mass - essentially which direction the Force is pointing.
Spring motion can be predicted using the momentum principle [math]\displaystyle{ dp=F_{net}*dt }[/math] and the position-update formula [math]\displaystyle{ dr= p_f/m*dt }[/math] Because spring motion involves oscillation, it is important to iterate with a small enough change in time to capture the full path of the spring-mass system.
A Computational Model
Follow the link to check out a 3D model of Spring Motion. The code displays a spring with one fixed end on a ceiling and a mass attached to the free end. https://trinket.io/glowscript/3587ff8cbe
The pink arrow represents the magnitude and direction of the mass's momentum. The yellow arrow represents the changing net force, Force of gravity + Force of the spring, on the mass (scaled down to 10%). Examine the orange curve after the simulation ends to follow the path of the mass's motion. Try an initial mass location to give a straight vertical path!
Spring Stiffness
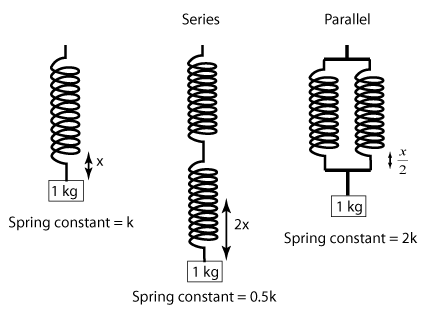
The spring stiffness [math]\displaystyle{ k_s }[/math] is a constant for each individual spring and is important for comparing the forces of different spring systems.
We can consider attaching multiple springs of the same length and stiffness in a system to create a new larger spring and examine the change in spring stiffness by measuring the distance stretched with the same force applied to the spring system.
For example, if you attach two of the same spring in parallel, the spring stiffness will be twice the value for one of the springs because you have to account for pulling against the force of two springs simultaneously.
However if you attach two of the same spring in series, the spring stiffness is half of what it is for one spring. This is because, for the same force, each spring stretches the same length as it would by itself.
Connectedness
Spring motion can be found throughout nature. If you consider the bouncing movement of kangaroos, you can use the concepts of spring motion to model the role of spring-like tendons in their hips.
History
This concept of motion stems directly from Sir Isaac Newton's Third Law of Motion: "For every action, there is an equal and opposite reaction" which was published in his work the Philosophiae Naturalis Principia Mathematica in 1687. This can be modeled well with a spring. As you (or gravity and a weighted mass) stretch one end of a spring, the spring pulls back based on our model of its force.

See also
Check out the Newton's Second Law: the Momentum Principle page to learn more about net force's affect on the momentum, velocity, and position of an object.
References
Editors, B. c. Isaac Newton Biography. from http://www.biography.com/people/isaac-newton-9422656
Elasticity. from http://www.one-school.net/Malaysia/UniversityandCollege/SPM/revisioncard/physics/forceandmotion/elasticity.html
Sound Propogation in Elastic Materials. from https://www.nde-ed.org/EducationResources/CommunityCollege/Ultrasonics/Physics/elasticsolids.htm