Point Charge: Difference between revisions

From Physics Book
Jump to navigation Jump to search
No edit summary
 
(230 intermediate revisions by 13 users not shown)
Line 1: Line 1:
Claimed by Gabriel Cruz Fall 2025
This page is all about the [[Electric Field]] due to a Point Charge.
This page is all about the [[Electric Field]] due to a Point Charge.


== Electric Field==


A Work In Progress by Brandon Weiner:  [[User:bweiner6|bweiner6]] ([[User talk:bweiner6|talk]])


===A Mathematical Model of Electric Field due to Point Charge===
==The Main Ideas ==
(Ch 13.1 in ''Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood'')
 
'''Point Charge / Particle''' — an object whose radius is extremely small compared to the distances to other objects in the system. Because it is so small, all of its charge and mass can be treated as if they are concentrated at a single point.
 
* Electrons and protons are always treated as point particles unless stated otherwise.
 
<u>Two types of point charges:</u> 
* **Protons ( +e )** → positive point charges, <math>q = +1.6\times10^{-19}\text{ C}</math> 
* **Electrons ( –e )** → negative point charges, <math>q = -1.6\times10^{-19}\text{ C}</math>
 
''Like'' point charges '''repel'''; ''opposite'' point charges '''attract'''.
 
<table border>
  <tr>
    <th>Point Charges</th>
    <th>Result</th>
    <th>Diagram</th>
  </tr>
  <tr>
    <td>1 proton, 1 electron</td>
    <td>Attract</td>
    <td>[[File:Proton_electron_attraction.png]]</td>
  </tr>
  <tr>
    <td>2 protons</td>
    <td>Repel</td>
    <td>[[File:Proton_repulsion.png]]</td>
  </tr>
  <tr>
    <td>2 electrons</td>
    <td>Repel</td>
    <td>[[File:Electron_repulsion.png]]</td>
  </tr>
</table border>
 
 
===The Electric Field===
(Ch 13.3 in ''Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood'')
 
The electric field describes how a source charge influences the space around it. This field exists everywhere, even if no other charges are present to experience a force. The electric field allows interactions to occur at a distance.
 
It is important to note that **electric field is not the same as electric force**.
 
Electric Force due to an Electric Field:
 
<math>\vec{F} = q\vec{E}</math>
 
* **F** = force on the particle 
* **E** = electric field at the observation location 
* **q** = charge of the particle (assume <math>1.6\times10^{-19}\text{ C}</math> unless stated otherwise)
 
The electric field becomes weaker as the distance from the point charge increases.
 
<table border>
  <tr>
    <td>The electric field of a positive point charge points radially outward.</td>
    <td>The electric field of a negative point charge points radially inward.</td>
  </tr>
  <tr>
    <td>[[File:Proton_electric_field.png]]</td>
    <td>[[File:Electron_electric_field.png]]</td>
  </tr>
</table border>
 
 
===A Mathematical Model===
 
====Electric Field Due to a Point Charge====
(Ch 13.4 in ''Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood'')
 
The magnitude of the electric field decreases with increasing distance from the point charge. This is described by:
 
<math>\vec{E} = \frac{1}{4\pi\epsilon_0}\frac{q}{|\vec{r}|^2}\hat{r}</math>  (Newtons/Coulomb)
 
* <math>\frac{1}{4\pi\epsilon_0}</math> is Coulomb’s constant, approximately <math>8.987\times10^{9}\frac{N\,m^2}{C^2}</math> 
* **q** = charge of the source particle 
* **r** = distance from source location to observation location 
* <math>\hat{r}</math> = unit vector pointing from the source to the observation point 
 
'''Reminder:''' <math>\hat{r}</math> always points from the source charge to the observation location.
 
The direction of the electric field depends on the sign of the source charge:
 
* If the source charge is positive → field points away (same direction as <math>\hat{r}</math>) 
* If the source charge is negative → field points toward the charge (opposite <math>\hat{r}</math>)


The Electric Field of a Point Charge can be found by the formula:
<math>\vec E=\frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} \hat r,\text{where } \frac{1}{4 \pi \epsilon_0 } \text{is approximately }  9*10^{9} \frac{N m^2}{C^2} \text{, q is the charge of the particle,}


\text{r is the magnitude of the distance}
====Coulomb Force Law for Point Charges====
\text{ between the point charge and the observation point, and }</math>  
(Ch 13.2 in ''Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood'')
<math>\hat r \text { is the direction of the distance from }
 
\text{the point charge to the observation point.}  
<math>|\vec{F}| = \frac{1}{4\pi\epsilon_0}\frac{|Q_1 Q_2|}{r^2}</math>
\text{ This equation becomes Coulomb's Law when multiplied by a second particles's charge. } </math>
 
Coulomb’s Law describes the magnitude of the electric force between two point charges.
 
The full vector form is:
 
<math>\vec{F} = \frac{1}{4\pi\epsilon_0}\frac{Q_1 Q_2}{r^2}\hat{r}</math>
 
* <math>Q_1, Q_2</math> = the charges 
* **r** = the distance between the two charges 
* <math>\frac{1}{4\pi\epsilon_0}</math> = Coulomb’s constant 
 
 
====Connection Between Electric Field and Force====
 
The force on a test charge is given by <math>F = Eq</math>.
 
Substituting Coulomb’s Law for **F**:
 
<math> E = \frac{F}{q_2} = \frac{1}{4\pi\epsilon_0}\frac{q_1}{r^2}\hat{r} </math>
 
The similarity of the Coulomb force law and electric field equation comes from the fact that the electric field is the force per unit test charge:
 
<math>\vec{E} = \frac{\vec{F}}{q_{test}}</math>
 
Direction rules:
 
* If the source charge is positive → force and field point away from the charge
* If the source charge is negative → force and field point toward the charge 
 
 
====Electric Field Superposition (Point Charges)====
 
When multiple point charges are present, the **net electric field** is the vector sum of the electric field from each charge:
 
<math>\vec{E}_{net} = \sum \vec{E}_i</math>
 
This is due to the principle of **superposition**: the total effect is the sum of individual effects.
 
Important reminders:
 
* A charge does not exert a force on itself  
* Source charges are assumed not to move (so <math>\vec{F}_{net} = 0</math>) 
 
[[File:IMG_1DCC0A11C7B8-1.jpeg]]


===A Computational Model===
===A Computational Model===


Here is a link to some code which shows the Electric Field due to an Proton at different points.  
Below is a simulation showing the electric field at various observation locations around a proton. The arrows decrease in size according to <math>\frac{1}{r^{2}}</math>, showing how the electric field weakens with distance.


<html> <iframe src="https://trinket.io/embed/glowscript/cf036f65f7?start=result" width="100%" height="600" frameborder="0" marginwidth="0" marginheight="0" allowfullscreen></iframe> </html>
[[File:First code.gif]]
 
Two adjacent point charges of opposite sign form an electric dipole. The electric field points toward the negative charge (blue) and away from the positive charge (red).
 
[[File:Code_2.png]]
 
===A Computational Model 2 ===
 
[https://trinket.io/glowscript/650fbf3a95c5 Click this link to see another computional model.]


==Examples==
==Examples==


===Simple===
There is an electron at the origin. Calculate the electric field at <4, -3, 1> m.


'''Problem 1:''' There is a proton at <1,2,3>. Calculate the electric field at <2,-1,3>.  
[[File:Screenshot_2024-04-13_160839.png]]


'''Step 1:''' Find <math>\hat r</math>
===Middling===
A particle of unknown charge is located at <-0.21, 0.02, 0.11> m. Its electric field at point <-0.02, 0.31, 0.28> m is <math><0.124, 0.188, 0.109> </math> N/C. Find the magnitude and sign of the particle's charge.


Find <math>\vec r_{obs} - \vec r_{proton}  (<2,-1,3> - <1,2,3> = <1,-3,0>) </math>
Given both an observation location and a source location, one can find both r and <math>\hat{r}</math>  Given the value of the electric field, one can also find the magnitude of the electric field. Then, using the equation for the magnitude of electric field of a point charge, <math> E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} </math> one can find the magnitude and sign of the charge.


Calculate the magnitude of r. (<math>\sqrt{1^2+(-3)^2+0^2}=\sqrt{10}</math>
<table border>
  <tr>
    <td> <b>Step 1.</b> Find <math>\vec r_{obs} - \vec r_{particle} </math>:


From r, find the unit vector <math>\hat{r}.</math> <math> <\frac{1}{\sqrt{10}},\frac{-3}{\sqrt{10}},\frac{0}{\sqrt{10}}> </math>
<math>\vec r = <-0.02, 0.31, 0.28> m - <-0.21, 0.02, 0.11> m = <0.19,0.29,0.17> m </math>


'''Step 2:''' Find the magnitude of the Electric Field
To find <math>\vec r_{mag} </math>, find the magnitude of <math><0.19,0.29,0.17></math>


<math> E= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} = \frac{1}{4 \pi \epsilon_0 } \frac{1.6 * 10^{-19}}{10} </math>  
<math>\sqrt{0.19^2+0.29^2+0.17^2}=\sqrt{0.1491}= 0.39</math>
</td></tr>


'''Step 3:''' Multiply the magnitude by <math>\hat{r}</math> to find the Electric Field
    <tr><td><b>Step 2:</b> Find the magnitude of the Electric Field:


E= <math> \frac{1}{4 \pi \epsilon_0 } \frac{1.6 * 10^{-19}}{10}*<\frac{1}{\sqrt{10}},\frac{-3}{\sqrt{10}},\frac{0}{\sqrt{10}}>=<4.554*10^{-11},-1.366*10^{-10},0>   N/C   </math>
<math>E= <0.124, 0.188, 0.109> N/C</math>  


<math>E_{mag} = (\sqrt{0.124^2+0.188^2+0.109^2}=\sqrt{0.0626}=0.25</math>  </td></tr>


'''Problem 2:'''
    <td>'''Step 3:''' Find '''''q''''' by rearranging the equation for <math>E_{mag}</math>


Once the basic equation and execution of Coulomb’s Law is understood, it can seem that problems with point charges cannot possibly get any harder. The three variables are Electric Field, charge, and distance between the charges. Any problem must provide two of the three, and the student “plugs and chugs” to get the third. It may seem that these problems could not possibly be made harder without looking at a bunch of point charges together in the shape of a disk or ring or rod. However, this is not true.
<math> E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} </math>


The variable that one often does not consider is that the third variable, distance between charges, is actually the negative summation of two variables, observation location and location of charge (or source location). Meaning, to know the distance between the charges (or the charge and wherever you are calculating the field), you must know both the observation location and where the charge is. The example problem below elucidates how this can become quite tricky.
By rearranging this equation we get


'''Problem''': There is a charged particle at an unknown location. Its charge is <math> Q </math> Coulombs. At location (<math>obs_{x}, obs_{y}, obs_{z}) </math> meters, an Electric Field of <math>(E_{x},E_{y},E_{z}) N/C </math> is observed. At what location is the charged particle? Assume the Electric Field is caused only by the single charged particle, no other charges are close.
<math> q= {4 \pi * \epsilon_0 } *{r^2}*E_{mag} </math>  
You could use your own made up values for the three givens, but for the solution we will us <math> Q = 2*10^{-8} </math> Coulombs, location is <math> (.26, .75, .09) </math> meters, and Electric Field is <math> (400,800,500) N/C </math>.


'''Solution''':
<math> q= {1/(9*10^9)} *{0.39^2}*0.25 </math>
First, I will summarize the steps. Then I will give a detailed explanation of why each step is the correct one, plugging in the numbers for the student to follow along with. The last part of the solution guide is a Matlab code that solves any inputs to this problem so the student can visualize the solving of the problem in a slightly different way, as well as generate nir own problems.  


'''Summary of Steps''':
<math> q= + 4.3*10^{-12} C </math></td>


Step 1: Find Magnitude of Electric Field by using Pythagorean Theorem on the components
</table border>


Step 2: Find Magnitude of <math>\vec r </math> (which is distance between charge and observation location) by rearranging Coulomb’s Law
===Difficult===
The electric force on a -2 mC particle at location (3.98, 3.98, 3.98) m due to a particle at the origin is  
<math>\langle -5.5\times10^{3},\, -5.5\times10^{3},\, -5.5\times10^{3}\rangle</math> N. 
What is the charge on the particle at the origin?


Step 3: Find unit vector of Electric Field
Given the force and the charge of the particle experiencing the force, we can first compute the electric field at the observation location. Once the electric field is known, we can use the point-charge electric field model to solve for the unknown source charge.


Step 4: Using sign of the charge and unit vector of Electric Field, find unit vector of <math>\vec r </math>
<table border>
  <tr>
    <td>
<b>Step 1.</b> Find the electric field using <math>\vec{F} = q\vec{E}</math>.


Step 5: Find the vector <math>\vec r </math> by multiplying the unit vector and magnitude of <math>\vec r </math>
<math>\vec{E} = \frac{\vec{F}}{q}</math>


Step 6: Solve for position of charge
<math> = \frac{\langle -5.5\times10^{3}, -5.5\times10^{3}, -5.5\times10^{3}\rangle}{-2\times10^{-3}}</math>


Detail Explanation with numbers:
<math> = \langle 2.75\times10^{6},\, 2.75\times10^{6},\, 2.75\times10^{6}\rangle</math> N/C
    </td>
  </tr>


First, let’s clarify what <math>\vec r </math> is. We observe an Electric Field, <math>\vec E </math>, at a given point; thus, this is the observation location. The distance from the charged particle to this observation location is <math>\vec r </math>. So for this problem, we know the observation location, but not where the charge is. Observation location is called <math> (obs_{x}, obs_{y}, obs_{z} </math>).
  <tr>
    <td>
<b>Step 2.</b> Compute <math>\vec{r}</math> from the particle at the origin to the observation location.


So:
<math>\vec{r} = \langle 3.98,\,3.98,\,3.98\rangle\ \text{m}</math>
<math> r = (obs_{x}, obs_{y}, obs_{z}) – (x, y, z)  </math>


Or in this case:
Magnitude:


<math> r = (.26,.75, .09) – (x,y,z) </math>
<math>|\vec{r}| = \sqrt{3.98^2 + 3.98^2 + 3.98^2}</math> 
<math>= \sqrt{47.52} \approx 6.89\ \text{m}</math>


The problem is asking us what (x,y,z) is, so to solve it, we must find <math>\vec r </math>.
Unit vector:


However, the issue is Coulomb’s Law doesn’t use r in vector form. It uses the magnitude of r and the unit vector of r, which from now on will be referred to as <math> r_{mag} </math> and <math>\hat{r} </math> respectively.
<math>\hat{r} = \frac{\vec{r}}{|\vec{r}|}</math>
    </td>
  </tr>


So to find r vector, we need both <math> r_{mag} </math> and <math>\hat{r} </math>
  <tr>
    <td>
<b>Step 3.</b> Solve for the unknown charge using the point-charge field equation:


Magnitude is easy because we can just use the magnitude version of Coulomb’s Law:
<math>E_{mag}=\frac{1}{4\pi\epsilon_0}\frac{|q|}{r^2}</math>


<math> E_{mag} = \frac{1}{4 \pi \epsilon_0} * \frac{q}{(rmag)^{2}} </math>
Rearranged:


We are given <math> q </math>, and <math> E_{mag} </math> can easily be calculated from the given <math>\vec E </math> using Pythagorean Theorem. And then we can rearrange Coulomb’s Law from above so that rmag is on one side of the equation.
<math>|q| = (4\pi\epsilon_0)\,(r^2)\,E_{mag}</math>


So:  
Using <math>E_{mag} = 2.75\times10^{6}</math> N/C and <math>r = 6.89</math> m:


<math> r_{mag} = \sqrt{\frac{1}{4 \pi \epsilon_0} * \frac{q}{E_{mag}}} </math>
<math>|q| = (8.99\times10^{-12})(6.89^2)(2.75\times10^{6})</math>


And with our numbers:
<math>|q| \approx 0.237\ \text{C}</math>


<math> r_{mag} = \sqrt{9*10^{9} * \frac{2*10^{-8}}{1024.7}} = .42 </math>
Sign of the charge: 
The force on the negative test charge is **toward** the origin → the source must be **positive**.


But how do we find <math>\hat{r} </math> so we can finish calculating the <math>\vec r </math>?
<b>Final Answer:</b> 
<math>q_{\text{origin}} \approx +0.24\ \text{C}</math>
    </td>
  </tr>
</table border>


Well, think about this. A unit vector is simply a way of mathematically describing direction. All of the direction of the Electric Field comes from the direction of the vector between the two locations, or <math>\vec r </math>. <math> Q </math> is a scalar and alters direction in no way, with one exception. All of the direction of <math>\vec E </math> comes from <math>\vec r </math>,then. Said mathematically, <math>\hat{E} </math> equals the absolute value of <math>\hat{r} </math>. Why absolute value? It is necessary because of the exception mentioned above. The charge can flip the direction of the field 180 degrees depending on its sign. Replacing a charged particle with a particle of the opposite sign results in an <math>\vec E </math> in the exact opposite direction, despite <math>\hat{r} </math> remaining the same.  
====Common Mistakes====
* **Using the wrong sign for q.** 
  Remember: if the force on a negative charge points toward the origin, the source must be positive.


So:
* **Forgetting that E and F point the same direction only for positive test charges.**
<math>\hat{E} = \frac{\vec E}{E_{mag}} = (400,800,500)/1024.7 = (.39,.78,.488) </math>
  Since the test charge is −2 mC, is opposite the force direction.
And q is positive:
<math>\hat{E} = (.39,.78,.488) </math>
<math> \vec r = \hat{r} * r_{mag} = (.39,.78,.488) * .42 = (.1638, .3276, .2058) </math>


Going back to our original equation:
* **Mixing up <math>\vec{r}</math> and <math>|\vec{r}|</math>.** 
<math> (.1638, .3276, .2058) = (.26,.75,.09) – (x,y,z) </math>
  One is a vector; the other is a scalar distance.
So the location of the charge is <math> (.096, .422, -.115) </math>


This problem can be solved instantaneously with this Matlab code, which take the inputs of E and observation location as six different scalars:
* **Failing to use the magnitude of E when solving for |q|.** 
  The field equation uses only magnitudes, not vector components.


    function [positionOfCharge] = Elec(Ex, Ey, Ez, obs_x, obs_y, obs_z, q)
* **Using an incorrect value of Coulomb’s constant.**
    Emag = (Ex^2 + Ey^2 + Ez^2)^(1/2);
    rmag = abs((9e9*q/Emag)^(1/2));
    Ehatx = Ex./Emag;
    Ehaty = Ey./Emag;
    Ehatz = Ez./Emag;
        if q < 0
            rhatx = -(Ehatx);
            rhaty = -(Ehaty);
            rhatz = -(Ehatz);
        elseif q > 0
            rhatx = Ehatx;
            rhaty = Ehaty;
            rhatz = Ehatz;
        end
    rx = rhatx * rmag;
    ry = rhaty * rmag;
    rz = rhatz * rmag;
    xpos = obs_x - rx;
    ypos = obs_y - ry;
    zpos = obs_z - rz;
    positionOfCharge = [xpos ypos zpos];
    end


==Connectedness==
==Connectedness==
1.How is this topic connected to something that you are interested in?
''1. How is this topic connected to something that you are interested in?''


I am very interested in the idea of forces and how objects interact with each other. After you calculate the Electric Field you can easily find the Electric Force one particle exerts on another.
The topic is fascinating because electric fields not only exist within the human body but also in the realms of aerospace. It's captivating to think about the parallels between biological systems and aerospace systems, where electric field management is crucial for functions such as propulsion and navigation. Analyzing how bodies maintain and adapt their electric fields and applying this knowledge to aerospace engineering can lead to innovative approaches to energy management and system efficiency, particularly in the face of perturbations such as equipment failure or external environmental factors.


2.How is it connected to your major?
''2. How is it connected to your major?''


I am a CompE major and so Electric Fields have to do with my major because when you integrate them with respect to dL, and swap the sign, you get potential difference(voltage), which is very important in circuits. As ECE majors take circuits classes, this topic is relevant to me.
As an aerospace engineer, my interest lies in the application of principles from various sciences, including biochemistry, to improve and innovate within the field of aviation and space exploration. Understanding the role of electric fields in cellular behavior provides insights into potential analogs in aerospace technology. For instance, similar to how cells adjust their electric fields for optimal function, aerospace systems must regulate their onboard electric fields for navigation, communication, and operational efficiency. Such interdisciplinary knowledge can be the foundation for advancements in aerospace materials and systems that are responsive and adaptive to their environments.  


3.Is there an interesting industrial application?
''3. Is there an interesting industrial application?''


An interesting application is that electric fields of point charges can be used to find forces. Then you can predict the motion of various particles by the forces acting on them.
PEMF (Pulsed Electromagnetic Field) therapy's principle of restoring optimal voltage in damaged cells through electromagnetic fields has interesting parallels in aerospace engineering. For example, the management of electromagnetic fields is critical in spacecraft and aircraft to protect onboard electronics and enhance communication signals. The concept of PEMF can inspire the development of systems that can self-regulate and optimize electrical potential across different components of an aircraft or spacecraft, thereby enhancing performance and resilience. Such systems could prove vital in long-duration space missions, where human intervention is limited, and the machine's ability to self-heal and maintain operational integrity can be a game-changer.


==History==
==History==
 
[[File:CoulombCharles300px.jpg]]
''Charles de Coulomb''
 
Charles de Coulomb was born in June 14, 1736 in central France. He spent much of his early life in the military and was placed in regions throughout the world. He only began to do scientific experiments out of curiously on his military expeditions. However, when controversy arrived with him and the French bureaucracy coupled with the French Revolution, Coulomb had to leave France and thus really began his scientific career.
 
Between 1785 and 1791, de Coulomb wrote several key papers centered around multiple relations of electricity and magnetism. This helped him develop the principle known as Coulomb's Law, which confirmed that the force between two electrical charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. This is the same relationship that is seen in the electric field equation of a point charge.


In the 1780s a French scientist named Charles Coulomb published many scientific papers on electricity and magnetism. While doing experiments, Coulomb had discovered an inverse square relationship between the amount of electric field and the distance between two particles and the electric field pointed in a line between the particles.  
[[File:Benjamin-Franklin-Portrait.png]]
''Benjamin Franklin''


Also, he discovered that the charge of an particle (ie. positive or negative) determined the direction of the electric field (either a repulsion or attraction).  
Benjamin Franklin (1706–1790) made several foundational contributions to the early understanding of electric charge. Although he did not write mathematical laws like Coulomb, his ideas directly shaped the concepts used in point-charge physics.


From these observations, as well as the use of fundamental constants, the equation of the electric field due to a point charge was created.
Franklin introduced the naming system of positive and negative charge, which is still used today. He proposed that charge behaves like a conserved quantity that can move between objects—an essential idea behind treating charges as isolated point charges located at specific positions in space.


== See also ==
== See also ==




[[Electric Field]] More general ideas about electric fields <br>
[[Electric Field]] <br>
[[Electric Force]] One application of electric fields due to point charges deals with finding electric force
[[Electric Force]] <br>
[[Superposition Principle]] <br>
[[Electric Dipole]]


===Further reading===
===Further reading===
Line 174: Line 316:
Principles of Electrodynamics by Melvin Schwartz
Principles of Electrodynamics by Melvin Schwartz
ISBN: 9780486134673
ISBN: 9780486134673
Electricity and Magnetism: Edition 3 , Edward M. Purcell David J. Morin


===External links===
===External links===


Some more information : http://hyperphysics.phy-astr.gsu.edu/hbase/electric/epoint.html
Some more information:
 
*http://www.physics.umd.edu/courses/Phys260/agashe/S10/notes/lecture18.pdf
*https://www.reliantphysicaltherapy.com/services/pulsed-electromagnetic-field-pemf
*https://www.youtube.com/watch?v=HG9KxDZ-qwI&t=1s
*https://www.youtube.com/watch?v=8GJf-Fj-qoI&t=3s


==References==
==References==


Matter and Interactions Vol. II
Chabay. (2000-2018). ''Matter & Interactions'' (4th ed.). John Wiley & Sons.
 


Charles-Augustin de Coulomb. (n.d.). Retrieved December 3, 2015, from https://nationalmaglab.org/education/magnet-academy/history-of-electricity-magnetism/pioneers/charles-augustin-de-coulomb
PY106 Notes. (n.d.). Retrieved November 27, 2016, from http://physics.bu.edu/~duffy/py106.html


Retrieved November 28, 2016, from http://www.biography.com/people/charles-de-coulomb-9259075#controversy-and-absolution


Shech, E., & Hatleback, E. (n.d.). The Material Intricacies of Coulomb’s 1785 Electric Torsion Balance Experiment. Retrieved December 3, 2015, from http://philsci-archive.pitt.edu/11048/1/The_Material_Intricacies_of_Coulomb's_1785_Electric_Torsion_Balance_Experiment_(EV).pdf




[[Category:Fields]]
[[Category:Fields]]

Latest revision as of 22:59, 23 November 2025

Claimed by Gabriel Cruz Fall 2025

This page is all about the Electric Field due to a Point Charge.


The Main Ideas

(Ch 13.1 in Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood)

Point Charge / Particle — an object whose radius is extremely small compared to the distances to other objects in the system. Because it is so small, all of its charge and mass can be treated as if they are concentrated at a single point.

  • Electrons and protons are always treated as point particles unless stated otherwise.

Two types of point charges:

  • **Protons ( +e )** → positive point charges, [math]\displaystyle{ q = +1.6\times10^{-19}\text{ C} }[/math]
  • **Electrons ( –e )** → negative point charges, [math]\displaystyle{ q = -1.6\times10^{-19}\text{ C} }[/math]

Like point charges repel; opposite point charges attract.

Point Charges Result Diagram
1 proton, 1 electron Attract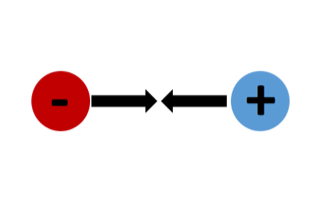
2 protons Repel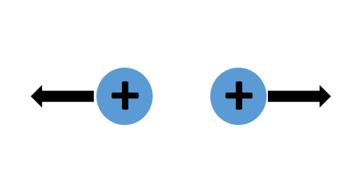
2 electrons Repel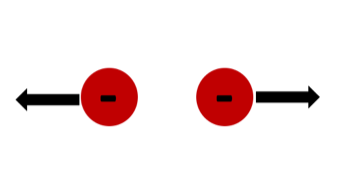


The Electric Field

(Ch 13.3 in Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood)

The electric field describes how a source charge influences the space around it. This field exists everywhere, even if no other charges are present to experience a force. The electric field allows interactions to occur at a distance.

It is important to note that **electric field is not the same as electric force**.

Electric Force due to an Electric Field:

[math]\displaystyle{ \vec{F} = q\vec{E} }[/math]

  • **F** = force on the particle
  • **E** = electric field at the observation location
  • **q** = charge of the particle (assume [math]\displaystyle{ 1.6\times10^{-19}\text{ C} }[/math] unless stated otherwise)

The electric field becomes weaker as the distance from the point charge increases.

The electric field of a positive point charge points radially outward. The electric field of a negative point charge points radially inward.


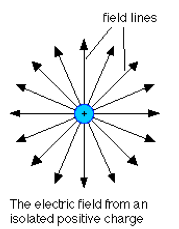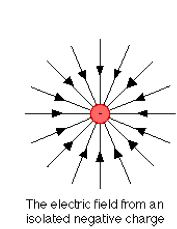A Mathematical Model

Electric Field Due to a Point Charge

(Ch 13.4 in Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood)

The magnitude of the electric field decreases with increasing distance from the point charge. This is described by:

[math]\displaystyle{ \vec{E} = \frac{1}{4\pi\epsilon_0}\frac{q}{|\vec{r}|^2}\hat{r} }[/math] (Newtons/Coulomb)

  • [math]\displaystyle{ \frac{1}{4\pi\epsilon_0} }[/math] is Coulomb’s constant, approximately [math]\displaystyle{ 8.987\times10^{9}\frac{N\,m^2}{C^2} }[/math]
  • **q** = charge of the source particle
  • **r** = distance from source location to observation location
  • [math]\displaystyle{ \hat{r} }[/math] = unit vector pointing from the source to the observation point

Reminder: [math]\displaystyle{ \hat{r} }[/math] always points from the source charge to the observation location.

The direction of the electric field depends on the sign of the source charge:

  • If the source charge is positive → field points away (same direction as [math]\displaystyle{ \hat{r} }[/math])
  • If the source charge is negative → field points toward the charge (opposite [math]\displaystyle{ \hat{r} }[/math])


Coulomb Force Law for Point Charges

(Ch 13.2 in Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood)

[math]\displaystyle{ |\vec{F}| = \frac{1}{4\pi\epsilon_0}\frac{|Q_1 Q_2|}{r^2} }[/math]

Coulomb’s Law describes the magnitude of the electric force between two point charges.

The full vector form is:

[math]\displaystyle{ \vec{F} = \frac{1}{4\pi\epsilon_0}\frac{Q_1 Q_2}{r^2}\hat{r} }[/math]

  • [math]\displaystyle{ Q_1, Q_2 }[/math] = the charges
  • **r** = the distance between the two charges
  • [math]\displaystyle{ \frac{1}{4\pi\epsilon_0} }[/math] = Coulomb’s constant


Connection Between Electric Field and Force

The force on a test charge is given by [math]\displaystyle{ F = Eq }[/math].

Substituting Coulomb’s Law for **F**:

[math]\displaystyle{ E = \frac{F}{q_2} = \frac{1}{4\pi\epsilon_0}\frac{q_1}{r^2}\hat{r} }[/math]

The similarity of the Coulomb force law and electric field equation comes from the fact that the electric field is the force per unit test charge:

[math]\displaystyle{ \vec{E} = \frac{\vec{F}}{q_{test}} }[/math]

Direction rules:

  • If the source charge is positive → force and field point away from the charge
  • If the source charge is negative → force and field point toward the charge


Electric Field Superposition (Point Charges)

When multiple point charges are present, the **net electric field** is the vector sum of the electric field from each charge:

[math]\displaystyle{ \vec{E}_{net} = \sum \vec{E}_i }[/math]

This is due to the principle of **superposition**: the total effect is the sum of individual effects.

Important reminders:

  • A charge does not exert a force on itself
  • Source charges are assumed not to move (so [math]\displaystyle{ \vec{F}_{net} = 0 }[/math])

A Computational Model

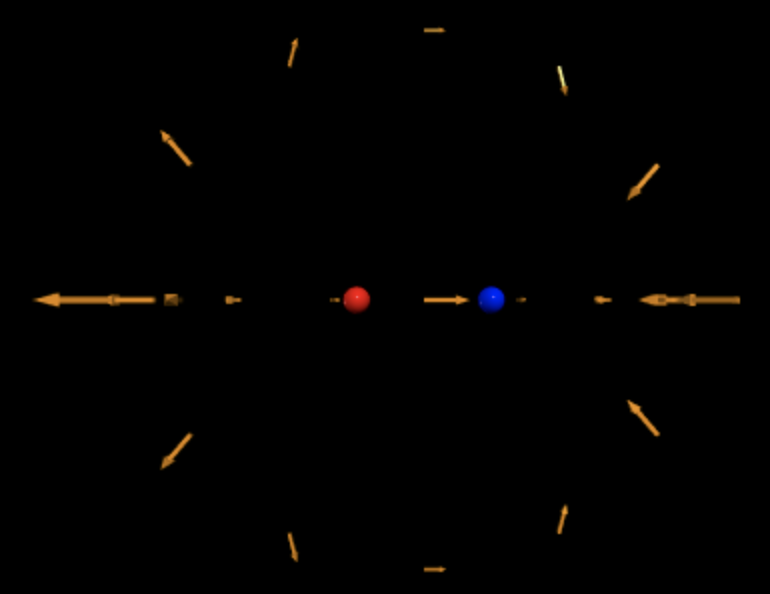
Below is a simulation showing the electric field at various observation locations around a proton. The arrows decrease in size according to [math]\displaystyle{ \frac{1}{r^{2}} }[/math], showing how the electric field weakens with distance.

Two adjacent point charges of opposite sign form an electric dipole. The electric field points toward the negative charge (blue) and away from the positive charge (red).

A Computational Model 2

Click this link to see another computional model.

Examples

Simple

There is an electron at the origin. Calculate the electric field at <4, -3, 1> m.

Middling

A particle of unknown charge is located at <-0.21, 0.02, 0.11> m. Its electric field at point <-0.02, 0.31, 0.28> m is [math]\displaystyle{ \lt 0.124, 0.188, 0.109\gt }[/math] N/C. Find the magnitude and sign of the particle's charge.

Given both an observation location and a source location, one can find both r and [math]\displaystyle{ \hat{r} }[/math] Given the value of the electric field, one can also find the magnitude of the electric field. Then, using the equation for the magnitude of electric field of a point charge, [math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math] one can find the magnitude and sign of the charge.

Step 1. Find [math]\displaystyle{ \vec r_{obs} - \vec r_{particle} }[/math]:

[math]\displaystyle{ \vec r = \lt -0.02, 0.31, 0.28\gt m - \lt -0.21, 0.02, 0.11\gt m = \lt 0.19,0.29,0.17\gt m }[/math]

To find [math]\displaystyle{ \vec r_{mag} }[/math], find the magnitude of [math]\displaystyle{ \lt 0.19,0.29,0.17\gt }[/math]

[math]\displaystyle{ \sqrt{0.19^2+0.29^2+0.17^2}=\sqrt{0.1491}= 0.39 }[/math]

Step 2: Find the magnitude of the Electric Field:

[math]\displaystyle{ E= \lt 0.124, 0.188, 0.109\gt N/C }[/math]

[math]\displaystyle{ E_{mag} = (\sqrt{0.124^2+0.188^2+0.109^2}=\sqrt{0.0626}=0.25 }[/math]
Step 3: Find q by rearranging the equation for [math]\displaystyle{ E_{mag} }[/math]

[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math]

By rearranging this equation we get

[math]\displaystyle{ q= {4 \pi * \epsilon_0 } *{r^2}*E_{mag} }[/math]

[math]\displaystyle{ q= {1/(9*10^9)} *{0.39^2}*0.25 }[/math]

[math]\displaystyle{ q= + 4.3*10^{-12} C }[/math]

Difficult

The electric force on a -2 mC particle at location (3.98, 3.98, 3.98) m due to a particle at the origin is [math]\displaystyle{ \langle -5.5\times10^{3},\, -5.5\times10^{3},\, -5.5\times10^{3}\rangle }[/math] N. What is the charge on the particle at the origin?

Given the force and the charge of the particle experiencing the force, we can first compute the electric field at the observation location. Once the electric field is known, we can use the point-charge electric field model to solve for the unknown source charge.

Step 1. Find the electric field using [math]\displaystyle{ \vec{F} = q\vec{E} }[/math].

[math]\displaystyle{ \vec{E} = \frac{\vec{F}}{q} }[/math]

[math]\displaystyle{ = \frac{\langle -5.5\times10^{3}, -5.5\times10^{3}, -5.5\times10^{3}\rangle}{-2\times10^{-3}} }[/math]

[math]\displaystyle{ = \langle 2.75\times10^{6},\, 2.75\times10^{6},\, 2.75\times10^{6}\rangle }[/math] N/C

Step 2. Compute [math]\displaystyle{ \vec{r} }[/math] from the particle at the origin to the observation location.

[math]\displaystyle{ \vec{r} = \langle 3.98,\,3.98,\,3.98\rangle\ \text{m} }[/math]

Magnitude:

[math]\displaystyle{ |\vec{r}| = \sqrt{3.98^2 + 3.98^2 + 3.98^2} }[/math] [math]\displaystyle{ = \sqrt{47.52} \approx 6.89\ \text{m} }[/math]

Unit vector:

[math]\displaystyle{ \hat{r} = \frac{\vec{r}}{|\vec{r}|} }[/math]

Step 3. Solve for the unknown charge using the point-charge field equation:

[math]\displaystyle{ E_{mag}=\frac{1}{4\pi\epsilon_0}\frac{|q|}{r^2} }[/math]

Rearranged:

[math]\displaystyle{ |q| = (4\pi\epsilon_0)\,(r^2)\,E_{mag} }[/math]

Using [math]\displaystyle{ E_{mag} = 2.75\times10^{6} }[/math] N/C and [math]\displaystyle{ r = 6.89 }[/math] m:

[math]\displaystyle{ |q| = (8.99\times10^{-12})(6.89^2)(2.75\times10^{6}) }[/math]

[math]\displaystyle{ |q| \approx 0.237\ \text{C} }[/math]

Sign of the charge: The force on the negative test charge is **toward** the origin → the source must be **positive**.

Final Answer: [math]\displaystyle{ q_{\text{origin}} \approx +0.24\ \text{C} }[/math]

Common Mistakes

  • **Using the wrong sign for q.**
 Remember: if the force on a negative charge points toward the origin, the source must be positive.
  • **Forgetting that E and F point the same direction only for positive test charges.**
 Since the test charge is −2 mC, is opposite the force direction.
  • **Mixing up [math]\displaystyle{ \vec{r} }[/math] and [math]\displaystyle{ |\vec{r}| }[/math].**
 One is a vector; the other is a scalar distance.
  • **Failing to use the magnitude of E when solving for |q|.**
 The field equation uses only magnitudes, not vector components.
  • **Using an incorrect value of Coulomb’s constant.**

Connectedness

1. How is this topic connected to something that you are interested in?

The topic is fascinating because electric fields not only exist within the human body but also in the realms of aerospace. It's captivating to think about the parallels between biological systems and aerospace systems, where electric field management is crucial for functions such as propulsion and navigation. Analyzing how bodies maintain and adapt their electric fields and applying this knowledge to aerospace engineering can lead to innovative approaches to energy management and system efficiency, particularly in the face of perturbations such as equipment failure or external environmental factors.

2. How is it connected to your major?

As an aerospace engineer, my interest lies in the application of principles from various sciences, including biochemistry, to improve and innovate within the field of aviation and space exploration. Understanding the role of electric fields in cellular behavior provides insights into potential analogs in aerospace technology. For instance, similar to how cells adjust their electric fields for optimal function, aerospace systems must regulate their onboard electric fields for navigation, communication, and operational efficiency. Such interdisciplinary knowledge can be the foundation for advancements in aerospace materials and systems that are responsive and adaptive to their environments.

3. Is there an interesting industrial application?

PEMF (Pulsed Electromagnetic Field) therapy's principle of restoring optimal voltage in damaged cells through electromagnetic fields has interesting parallels in aerospace engineering. For example, the management of electromagnetic fields is critical in spacecraft and aircraft to protect onboard electronics and enhance communication signals. The concept of PEMF can inspire the development of systems that can self-regulate and optimize electrical potential across different components of an aircraft or spacecraft, thereby enhancing performance and resilience. Such systems could prove vital in long-duration space missions, where human intervention is limited, and the machine's ability to self-heal and maintain operational integrity can be a game-changer.

History

Charles de Coulomb

Charles de Coulomb was born in June 14, 1736 in central France. He spent much of his early life in the military and was placed in regions throughout the world. He only began to do scientific experiments out of curiously on his military expeditions. However, when controversy arrived with him and the French bureaucracy coupled with the French Revolution, Coulomb had to leave France and thus really began his scientific career.

Between 1785 and 1791, de Coulomb wrote several key papers centered around multiple relations of electricity and magnetism. This helped him develop the principle known as Coulomb's Law, which confirmed that the force between two electrical charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. This is the same relationship that is seen in the electric field equation of a point charge.

Benjamin Franklin

Benjamin Franklin (1706–1790) made several foundational contributions to the early understanding of electric charge. Although he did not write mathematical laws like Coulomb, his ideas directly shaped the concepts used in point-charge physics.

Franklin introduced the naming system of positive and negative charge, which is still used today. He proposed that charge behaves like a conserved quantity that can move between objects—an essential idea behind treating charges as isolated point charges located at specific positions in space.

See also

Electric Field
Electric Force
Superposition Principle
Electric Dipole

Further reading

Principles of Electrodynamics by Melvin Schwartz ISBN: 9780486134673

Electricity and Magnetism: Edition 3 , Edward M. Purcell David J. Morin

External links

Some more information:

References

Chabay. (2000-2018). Matter & Interactions (4th ed.). John Wiley & Sons.

PY106 Notes. (n.d.). Retrieved November 27, 2016, from http://physics.bu.edu/~duffy/py106.html

Retrieved November 28, 2016, from http://www.biography.com/people/charles-de-coulomb-9259075#controversy-and-absolution

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Point_Charge&oldid=47362"