Point Charge: Difference between revisions

Latest revision as of 22:59, 23 November 2025

Claimed by Gabriel Cruz Fall 2025

This page is all about the Electric Field due to a Point Charge.

The Main Ideas

(Ch 13.1 in Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood)

Point Charge / Particle — an object whose radius is extremely small compared to the distances to other objects in the system. Because it is so small, all of its charge and mass can be treated as if they are concentrated at a single point.

Electrons and protons are always treated as point particles unless stated otherwise.

Two types of point charges:

**Protons ( +e )** → positive point charges, [math]\displaystyle{ q = +1.6\times10^{-19}\text{ C} }[/math]
**Electrons ( –e )** → negative point charges, [math]\displaystyle{ q = -1.6\times10^{-19}\text{ C} }[/math]

Like point charges repel; opposite point charges attract.

Point Charges	Result	Diagram
1 proton, 1 electron	Attract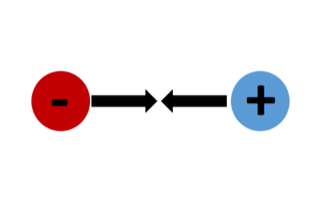
2 protons	Repel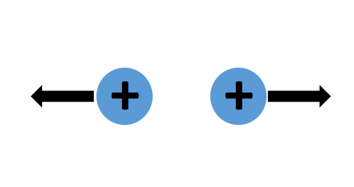
2 electrons	Repel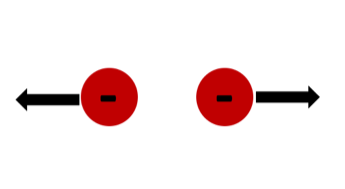

The Electric Field

(Ch 13.3 in Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood)

The electric field describes how a source charge influences the space around it. This field exists everywhere, even if no other charges are present to experience a force. The electric field allows interactions to occur at a distance.

It is important to note that **electric field is not the same as electric force**.

Electric Force due to an Electric Field:

[math]\displaystyle{ \vec{F} = q\vec{E} }[/math]

**F** = force on the particle
**E** = electric field at the observation location
**q** = charge of the particle (assume [math]\displaystyle{ 1.6\times10^{-19}\text{ C} }[/math] unless stated otherwise)

The electric field becomes weaker as the distance from the point charge increases.

The electric field of a positive point charge points radially outward.	The electric field of a negative point charge points radially inward.

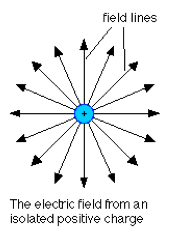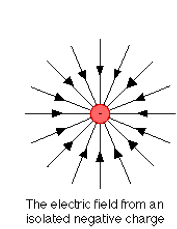A Mathematical Model

Electric Field Due to a Point Charge

(Ch 13.4 in Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood)

The magnitude of the electric field decreases with increasing distance from the point charge. This is described by:

[math]\displaystyle{ \vec{E} = \frac{1}{4\pi\epsilon_0}\frac{q}{|\vec{r}|^2}\hat{r} }[/math] (Newtons/Coulomb)

[math]\displaystyle{ \frac{1}{4\pi\epsilon_0} }[/math] is Coulomb’s constant, approximately [math]\displaystyle{ 8.987\times10^{9}\frac{N\,m^2}{C^2} }[/math]
**q** = charge of the source particle
**r** = distance from source location to observation location
[math]\displaystyle{ \hat{r} }[/math] = unit vector pointing from the source to the observation point

Reminder: [math]\displaystyle{ \hat{r} }[/math] always points from the source charge to the observation location.

The direction of the electric field depends on the sign of the source charge:

If the source charge is positive → field points away (same direction as [math]\displaystyle{ \hat{r} }[/math])
If the source charge is negative → field points toward the charge (opposite [math]\displaystyle{ \hat{r} }[/math])

Coulomb Force Law for Point Charges

(Ch 13.2 in Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood)

[math]\displaystyle{ |\vec{F}| = \frac{1}{4\pi\epsilon_0}\frac{|Q_1 Q_2|}{r^2} }[/math]

Coulomb’s Law describes the magnitude of the electric force between two point charges.

The full vector form is:

[math]\displaystyle{ \vec{F} = \frac{1}{4\pi\epsilon_0}\frac{Q_1 Q_2}{r^2}\hat{r} }[/math]

[math]\displaystyle{ Q_1, Q_2 }[/math] = the charges
**r** = the distance between the two charges
[math]\displaystyle{ \frac{1}{4\pi\epsilon_0} }[/math] = Coulomb’s constant

Connection Between Electric Field and Force

The force on a test charge is given by [math]\displaystyle{ F = Eq }[/math].

Substituting Coulomb’s Law for **F**:

[math]\displaystyle{ E = \frac{F}{q_2} = \frac{1}{4\pi\epsilon_0}\frac{q_1}{r^2}\hat{r} }[/math]

The similarity of the Coulomb force law and electric field equation comes from the fact that the electric field is the force per unit test charge:

[math]\displaystyle{ \vec{E} = \frac{\vec{F}}{q_{test}} }[/math]

Direction rules:

If the source charge is positive → force and field point away from the charge
If the source charge is negative → force and field point toward the charge

Electric Field Superposition (Point Charges)

When multiple point charges are present, the **net electric field** is the vector sum of the electric field from each charge:

[math]\displaystyle{ \vec{E}_{net} = \sum \vec{E}_i }[/math]

This is due to the principle of **superposition**: the total effect is the sum of individual effects.

Important reminders:

A charge does not exert a force on itself
Source charges are assumed not to move (so [math]\displaystyle{ \vec{F}_{net} = 0 }[/math])

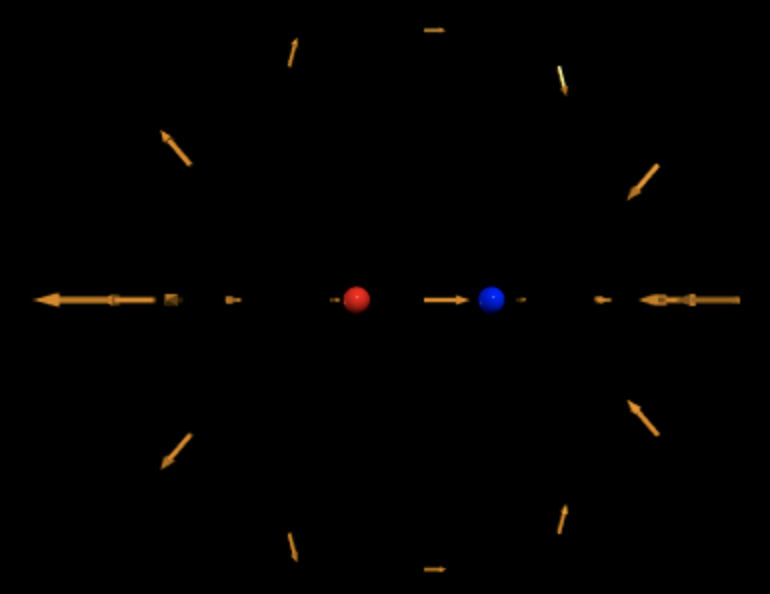
A Computational Model

Below is a simulation showing the electric field at various observation locations around a proton. The arrows decrease in size according to [math]\displaystyle{ \frac{1}{r^{2}} }[/math], showing how the electric field weakens with distance.

Two adjacent point charges of opposite sign form an electric dipole. The electric field points toward the negative charge (blue) and away from the positive charge (red).

A Computational Model 2

Click this link to see another computional model.

Examples

Simple

There is an electron at the origin. Calculate the electric field at <4, -3, 1> m.

Middling

A particle of unknown charge is located at <-0.21, 0.02, 0.11> m. Its electric field at point <-0.02, 0.31, 0.28> m is [math]\displaystyle{ \lt 0.124, 0.188, 0.109\gt }[/math] N/C. Find the magnitude and sign of the particle's charge.

Given both an observation location and a source location, one can find both r and [math]\displaystyle{ \hat{r} }[/math] Given the value of the electric field, one can also find the magnitude of the electric field. Then, using the equation for the magnitude of electric field of a point charge, [math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math] one can find the magnitude and sign of the charge.

Step 1. Find [math]\displaystyle{ \vec r_{obs} - \vec r_{particle} }[/math]:

[math]\displaystyle{ \vec r = \lt -0.02, 0.31, 0.28\gt m - \lt -0.21, 0.02, 0.11\gt m = \lt 0.19,0.29,0.17\gt m }[/math]

To find [math]\displaystyle{ \vec r_{mag} }[/math], find the magnitude of [math]\displaystyle{ \lt 0.19,0.29,0.17\gt }[/math]

[math]\displaystyle{ \sqrt{0.19^2+0.29^2+0.17^2}=\sqrt{0.1491}= 0.39 }[/math]

Step 2: Find the magnitude of the Electric Field:

[math]\displaystyle{ E= \lt 0.124, 0.188, 0.109\gt N/C }[/math]

[math]\displaystyle{ E_{mag} = (\sqrt{0.124^2+0.188^2+0.109^2}=\sqrt{0.0626}=0.25 }[/math]

Step 3: Find q by rearranging the equation for [math]\displaystyle{ E_{mag} }[/math]

[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math]

By rearranging this equation we get

[math]\displaystyle{ q= {4 \pi * \epsilon_0 } *{r^2}*E_{mag} }[/math]

[math]\displaystyle{ q= {1/(9*10^9)} *{0.39^2}*0.25 }[/math]

[math]\displaystyle{ q= + 4.3*10^{-12} C }[/math]

Difficult

The electric force on a -2 mC particle at location (3.98, 3.98, 3.98) m due to a particle at the origin is [math]\displaystyle{ \langle -5.5\times10^{3},\, -5.5\times10^{3},\, -5.5\times10^{3}\rangle }[/math] N. What is the charge on the particle at the origin?

Given the force and the charge of the particle experiencing the force, we can first compute the electric field at the observation location. Once the electric field is known, we can use the point-charge electric field model to solve for the unknown source charge.

Step 1. Find the electric field using [math]\displaystyle{ \vec{F} = q\vec{E} }[/math].

[math]\displaystyle{ \vec{E} = \frac{\vec{F}}{q} }[/math]

[math]\displaystyle{ = \frac{\langle -5.5\times10^{3}, -5.5\times10^{3}, -5.5\times10^{3}\rangle}{-2\times10^{-3}} }[/math]

[math]\displaystyle{ = \langle 2.75\times10^{6},\, 2.75\times10^{6},\, 2.75\times10^{6}\rangle }[/math] N/C

Step 2. Compute [math]\displaystyle{ \vec{r} }[/math] from the particle at the origin to the observation location.

[math]\displaystyle{ \vec{r} = \langle 3.98,\,3.98,\,3.98\rangle\ \text{m} }[/math]

Magnitude:

[math]\displaystyle{ |\vec{r}| = \sqrt{3.98^2 + 3.98^2 + 3.98^2} }[/math] [math]\displaystyle{ = \sqrt{47.52} \approx 6.89\ \text{m} }[/math]

Unit vector:

[math]\displaystyle{ \hat{r} = \frac{\vec{r}}{|\vec{r}|} }[/math]

Step 3. Solve for the unknown charge using the point-charge field equation:

[math]\displaystyle{ E_{mag}=\frac{1}{4\pi\epsilon_0}\frac{|q|}{r^2} }[/math]

Rearranged:

[math]\displaystyle{ |q| = (4\pi\epsilon_0)\,(r^2)\,E_{mag} }[/math]

Using [math]\displaystyle{ E_{mag} = 2.75\times10^{6} }[/math] N/C and [math]\displaystyle{ r = 6.89 }[/math] m:

[math]\displaystyle{ |q| = (8.99\times10^{-12})(6.89^2)(2.75\times10^{6}) }[/math]

[math]\displaystyle{ |q| \approx 0.237\ \text{C} }[/math]

Sign of the charge: The force on the negative test charge is **toward** the origin → the source must be **positive**.

Final Answer: [math]\displaystyle{ q_{\text{origin}} \approx +0.24\ \text{C} }[/math]

Common Mistakes

**Using the wrong sign for q.**

 Remember: if the force on a negative charge points toward the origin, the source must be positive.

**Forgetting that E and F point the same direction only for positive test charges.**

 Since the test charge is −2 mC, is opposite the force direction.

**Mixing up [math]\displaystyle{ \vec{r} }[/math] and [math]\displaystyle{ |\vec{r}| }[/math].**

 One is a vector; the other is a scalar distance.

**Failing to use the magnitude of E when solving for |q|.**

 The field equation uses only magnitudes, not vector components.

**Using an incorrect value of Coulomb’s constant.**

Connectedness

1. How is this topic connected to something that you are interested in?

The topic is fascinating because electric fields not only exist within the human body but also in the realms of aerospace. It's captivating to think about the parallels between biological systems and aerospace systems, where electric field management is crucial for functions such as propulsion and navigation. Analyzing how bodies maintain and adapt their electric fields and applying this knowledge to aerospace engineering can lead to innovative approaches to energy management and system efficiency, particularly in the face of perturbations such as equipment failure or external environmental factors.

2. How is it connected to your major?

As an aerospace engineer, my interest lies in the application of principles from various sciences, including biochemistry, to improve and innovate within the field of aviation and space exploration. Understanding the role of electric fields in cellular behavior provides insights into potential analogs in aerospace technology. For instance, similar to how cells adjust their electric fields for optimal function, aerospace systems must regulate their onboard electric fields for navigation, communication, and operational efficiency. Such interdisciplinary knowledge can be the foundation for advancements in aerospace materials and systems that are responsive and adaptive to their environments.

3. Is there an interesting industrial application?

PEMF (Pulsed Electromagnetic Field) therapy's principle of restoring optimal voltage in damaged cells through electromagnetic fields has interesting parallels in aerospace engineering. For example, the management of electromagnetic fields is critical in spacecraft and aircraft to protect onboard electronics and enhance communication signals. The concept of PEMF can inspire the development of systems that can self-regulate and optimize electrical potential across different components of an aircraft or spacecraft, thereby enhancing performance and resilience. Such systems could prove vital in long-duration space missions, where human intervention is limited, and the machine's ability to self-heal and maintain operational integrity can be a game-changer.

History

Charles de Coulomb

Charles de Coulomb was born in June 14, 1736 in central France. He spent much of his early life in the military and was placed in regions throughout the world. He only began to do scientific experiments out of curiously on his military expeditions. However, when controversy arrived with him and the French bureaucracy coupled with the French Revolution, Coulomb had to leave France and thus really began his scientific career.

Between 1785 and 1791, de Coulomb wrote several key papers centered around multiple relations of electricity and magnetism. This helped him develop the principle known as Coulomb's Law, which confirmed that the force between two electrical charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. This is the same relationship that is seen in the electric field equation of a point charge.

Benjamin Franklin

Benjamin Franklin (1706–1790) made several foundational contributions to the early understanding of electric charge. Although he did not write mathematical laws like Coulomb, his ideas directly shaped the concepts used in point-charge physics.

Franklin introduced the naming system of positive and negative charge, which is still used today. He proposed that charge behaves like a conserved quantity that can move between objects—an essential idea behind treating charges as isolated point charges located at specific positions in space.

Retrieved November 28, 2016, from http://www.biography.com/people/charles-de-coulomb-9259075#controversy-and-absolution

Point Charge: Difference between revisions

Latest revision as of 22:59, 23 November 2025

Contents

The Main Ideas

The Electric Field

A Mathematical Model

Electric Field Due to a Point Charge

Coulomb Force Law for Point Charges

Connection Between Electric Field and Force

Electric Field Superposition (Point Charges)

A Computational Model

A Computational Model 2

Examples

Simple

Middling

Difficult

Common Mistakes

Connectedness

History

See also

Further reading

External links

References

Navigation menu

@@ Line 1: / Line 1: @@
-Claimed by Machayla Randall Fall 2023
+Claimed by Gabriel Cruz Fall 2025
 This page is all about the [[Electric Field]] due to a Point Charge.
@@ Line 8: / Line 8: @@
 (Ch 13.1 in ''Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood'')
-'''Point Charge/Particle''' - an object with a radius that is very small compared to the distance between it and any other objects of interest in the system. Since it is very small, the object can be treated as if all of its charge and mass are concentrated at a single "point".
+'''Point Charge / Particle''' — an object whose radius is extremely small compared to the distances to other objects in the system. Because it is so small, all of its charge and mass can be treated as if they are concentrated at a single point.
-*Electrons and Protons are always considered to be point particles unless stated otherwise
-<u> 2 types of point charges: </u>
+* Electrons and protons are always treated as point particles unless stated otherwise.
-*Protons (e) --> positive point charges, ( q = 1.6e-19 Coulombs)
-*Electrons (-e) --> negative point charges, (q = -1.6e-19 Coulombs)
+<u>Two types of point charges:</u>
+* **Protons ( +e )** → positive point charges, <math>q = +1.6\times10^{-19}\text{ C}</math>
+* **Electrons ( –e )** → negative point charges, <math>q = -1.6\times10^{-19}\text{ C}</math>
-''Like'' point charges ''attract'', ''opposite'' point charges ''repel''.
+''Like'' point charges '''repel'''; ''opposite'' point charges '''attract'''.
-ex.<table border>  <tr>
-     <th> Point Charges </th>
+<table border>
-     <th> Result </th>
+  <tr>
-<th>Diagram</th>
+     <th>Point Charges</th>
+     <th>Result</th>
+    <th>Diagram</th>
    </tr>
    <tr>
-     <td> 1 proton, 1 electron</td>
+     <td>1 proton, 1 electron</td>
-     <td> Attract </td>
+     <td>Attract</td>
-<td>[[File:Proton_electron_attraction.png]]</td>
+    <td>[[File:Proton_electron_attraction.png]]</td>
    </tr>
    <tr>
-     <td>2 protons </td>
+     <td>2 protons</td>
-     <td> Repel </td>
+     <td>Repel</td>
-<td>[[File:Proton_repulsion.png]]</td>
+    <td>[[File:Proton_repulsion.png]]</td>
    </tr>
    <tr>
-     <td>2 electrons </td>
+     <td>2 electrons</td>
-     <td> Repel </td>
+     <td>Repel</td>
-<td>[[File:Electron_repulsion.png]]</td>
+    <td>[[File:Electron_repulsion.png]]</td>
    </tr>
 </table border>
 ===The Electric Field===
 (Ch 13.3 in ''Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood'')
-In general, the electric field evaluates the affect of the source on the surrounding objects and area. The electric field created by a charge is present throughout space at all times, whether or not there is another charge around to feel its effects. Therefore, the concept of the electric field by a point charge describes the interactions that can happen at a distance, due to these affects caused by this point charge.
+The electric field describes how a source charge influences the space around it. This field exists everywhere, even if no other charges are present to experience a force. The electric field allows interactions to occur at a distance.
-Important to differentiate that Electric Force does not equal the Electric Field.
+It is important to note that **electric field is not the same as electric force**.
-Electric Field of a Charge Observed at a location: F = Eq
+Electric Force due to an Electric Field:
-*F = Force on particle
-*E = electric field at source location
+<math>\vec{F} = q\vec{E}</math>
-*q = magnitude of the charge of particle (assume q= 1.6 x 10^-19)
-The magnitude of the electric field decreases with increasing distance from the point charge.
+* **F** = force on the particle
+* **E** = electric field at the observation location
+* **q** = charge of the particle (assume <math>1.6\times10^{-19}\text{ C}</math> unless stated otherwise)
+The electric field becomes weaker as the distance from the point charge increases.
 <table border>
    <tr>
-     <td>The electric field of a positive point charge points radially outward</td>
+     <td>The electric field of a positive point charge points radially outward.</td>
-     <td>The electric field of a negative point charge points radially inward</td>
+     <td>The electric field of a negative point charge points radially inward.</td>
    </tr>
    <tr>
-     <td>[[File:Proton_electric_field.png]] </td>
+     <td>[[File:Proton_electric_field.png]]</td>
-     <td> [[File:Electron_electric_field.png]] </td>
+     <td>[[File:Electron_electric_field.png]]</td>
    </tr>
 </table border>
 ===A Mathematical Model===
-====Electric Field due to Point Charge====
+====Electric Field Due to a Point Charge====
 (Ch 13.4 in ''Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood'')
-The magnitude of the electric field decreases with increasing distance from the point charge. This is described by the equation below:
+The magnitude of the electric field decreases with increasing distance from the point charge. This is described by:
-Electric Field of a Point Charge (<math>\vec E</math>):
+<math>\vec{E} = \frac{1}{4\pi\epsilon_0}\frac{q}{|\vec{r}|^2}\hat{r}</math>  (Newtons/Coulomb)
-<math>\vec E=\frac{1}{4 \pi \epsilon_0 } \frac{q}{\mid\vec r\mid ^2} \hat r</math> (Newtons/Coulomb)
+* <math>\frac{1}{4\pi\epsilon_0}</math> is Coulomb’s constant, approximately <math>8.987\times10^{9}\frac{N\,m^2}{C^2}</math>
+* **q** = charge of the source particle
+* **r** = distance from source location to observation location
+* <math>\hat{r}</math> = unit vector pointing from the source to the observation point
-*<math>\frac{1}{4 \pi \epsilon_0 } </math> is Coulomb's Constant and is approximately <math>8.987*10^{9}\frac{N m^2}{C^2} </math>
+'''Reminder:''' <math>\hat{r}</math> always points from the source charge to the observation location.
-*'''''q''''' is the charge of the particle
-*'''''r''''' is the magnitude of the distance between the observation location and the source location
-*<math>\hat r </math> is the unit vector in the direction of the distance from the source location to the observation point.
+The direction of the electric field depends on the sign of the source charge:
+* If the source charge is positive → field points away (same direction as <math>\hat{r}</math>)
+* If the source charge is negative → field points toward the charge (opposite <math>\hat{r}</math>)
-The direction of the electric field at the observation location depends on the both the direction of <math>\hat r </math> and the sign of the source charge.
-*If the source charge is positive, the field points away from the source charge.
-*If the source charge is negative, the field points toward the source charge.
 ====Coulomb Force Law for Point Charges====
 (Ch 13.2 in ''Matter & Interactions Vol. 2: Modern Mechanics, 4th Edition by R. Chabay & B. Sherwood'')
-<math>\mid\vec F\mid=\frac{1}{4 \pi \epsilon_0 } \frac{\mid Q_1Q_2 \mid}{r^2}</math>
+<math>|\vec{F}| = \frac{1}{4\pi\epsilon_0}\frac{|Q_1 Q_2|}{r^2}</math>
+Coulomb’s Law describes the magnitude of the electric force between two point charges.
+The full vector form is:
+<math>\vec{F} = \frac{1}{4\pi\epsilon_0}\frac{Q_1 Q_2}{r^2}\hat{r}</math>
-Coulomb's law is one of the four fundamental physical interactions, and it describes the magnitude of the electric force between two point-charges.
+* <math>Q_1, Q_2</math> = the charges
-<math>Q_1, Q_2</math>= The charge of two particles of interest
+* **r** = the distance between the two charges
+* <math>\frac{1}{4\pi\epsilon_0}</math> = Coulomb’s constant
-*<math>\mid\vec F\mid=\frac{1}{4 \pi \epsilon_0 }</math> = constant,
-* <math>Q_1, Q_2</math> = the magnitudes of the point charges
-*r = The distance between the two particles
 ====Connection Between Electric Field and Force====
-The force on a source charge is determined by <math> F = Eq </math> where '''''E''''' is the electric field and '''''q''''' is the charge of a test charge in Coulombs.
-By solving for the electric field in <math> F = Eq </math>, with F modeled by Coulomb's Law, you get the equation for the electric field of the point charge:
+The force on a test charge is given by <math>F = Eq</math>.
+Substituting Coulomb’s Law for **F**:
+<math> E = \frac{F}{q_2} = \frac{1}{4\pi\epsilon_0}\frac{q_1}{r^2}\hat{r} </math>
+The similarity of the Coulomb force law and electric field equation comes from the fact that the electric field is the force per unit test charge:
+<math>\vec{E} = \frac{\vec{F}}{q_{test}}</math>
+Direction rules:
-<math> E = \frac{F}{q_2} = \frac{1}{4 \pi \epsilon_0 } \frac{q_1q_2}{r^2}\frac{1}{q_2}\hat r  = \frac{1}{4 \pi \epsilon_0 } \frac{q_1}{r^2} \hat r </math>
+* If the source charge is positive → force and field point away from the charge
+* If the source charge is negative → force and field point toward the charge
-===A Computational Model===
-Below is a link to a code which can help visualize the Electric Field at various observation locations due to a proton. Notice how the arrows decrease in size by a factor of <math> \frac{1}{r^{2}} </math> as the observation location gets farther from the proton. The magnitude of the electric field decreases as the distance to the observation location increases.
+====Electric Field Superposition (Point Charges)====
+When multiple point charges are present, the **net electric field** is the vector sum of the electric field from each charge:
-[[File:First code.gif]]
+<math>\vec{E}_{net} = \sum \vec{E}_i</math>
-Two adjacent point charges of opposite sign exhibit an electric field pattern that is characteristic of a dipole. This interaction is displayed in the code below. Notice how the electric field points towards the negatively charged point charge (blue) and away from the positively charged point charge (red).
+This is due to the principle of **superposition**: the total effect is the sum of individual effects.
-[[File:Code_2.png]]
+Important reminders:
-==Examples==
+* A charge does not exert a force on itself
+* Source charges are assumed not to move (so <math>\vec{F}_{net} = 0</math>)
-===Simple===
+[[File:IMG_1DCC0A11C7B8-1.jpeg]]
-There is an electron at the origin. Calculate the electric field at <4, -3, 1> m.
-<table border>
+===A Computational Model===
-  <tr>
-    <td> <b>Step 1.</b> Find <math>\hat r</math>
-Find <math>\vec r_{obs} - \vec r_{electron}:
-((4,-3,1) - (0,0,0) = <4,-3,1> </math>m.
+Below is a simulation showing the electric field at various observation locations around a proton. The arrows decrease in size according to <math>\frac{1}{r^{2}}</math>, showing how the electric field weakens with distance.
-Calculate the magnitude of <math>\vec r</math>:
+[[File:First code.gif]]
-(<math>\sqrt{4^2+(-3)^2+1^2}=\sqrt{26}</math> From <math>\vec r</math>, find the unit vector <math>\hat{r}.</math> <math>  <\frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}> </math>
+Two adjacent point charges of opposite sign form an electric dipole. The electric field points toward the negative charge (blue) and away from the positive charge (red).
-</td></tr>
-    <tr><td>'''Step 2:''' Find the magnitude of the Electric Field
+[[File:Code_2.png]]
+===A Computational Model 2 ===
-<math> E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} = \frac{1}{4 \pi \epsilon_0 } \frac{-1.6 * 10^{-19}}{26} </math> </td>
+[https://trinket.io/glowscript/650fbf3a95c5 Click this link to see another computional model.]
-    <td>  </td></tr>
-    <td>'''Step 3:''' Multiply the magnitude of the Electric Field by <math>\hat{r}</math> to find the Electric Field
+==Examples==
-<math>E =  \frac{1}{4 \pi \epsilon_0 } \frac{-1.6 * 10^{-19}}{26}*<\frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}>
+===Simple===
+There is an electron at the origin. Calculate the electric field at <4, -3, 1> m.
-= <-4.34*10^{-11},3.26*10^{-11},-1.09*10^{-11}>   N/C    </math></td>
+[[File:Screenshot_2024-04-13_160839.png]]
-</table border>
 ===Middling===
@@ Line 183: / Line 200: @@
 ===Difficult===
-The electric force on a -2mC particle at a location (3.98 , 3.98 , 3.98) m due to a particle at the origin is <math>< -5.5*10^{3} , -5.5*10^{3}, -5.5*10^{3}></math> N. What is the charge on the particle at the origin?
+The electric force on a -2 mC particle at location (3.98, 3.98, 3.98) m due to a particle at the origin is
+<math>\langle -5.5\times10^{3},\, -5.5\times10^{3},\, -5.5\times10^{3}\rangle</math> N.
+What is the charge on the particle at the origin?
-Given the force and charge on the particle, one can calculate the surrounding electric field. With this variable found, this problem becomes much like the last one.
+Given the force and the charge of the particle experiencing the force, we can first compute the electric field at the observation location. Once the electric field is known, we can use the point-charge electric field model to solve for the unknown source charge.
-<math> E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r_{mag}^2} </math> to find the rmag value. To find <math>\hat r</math> we can find the direction of the electric field as that is obviously going to be in the same direction as  <math>\hat r</math>. Then, once we find  <math>\hat r</math>, all that is left to do is multiply <math>\hat r</math> by rmag and that will give us the  <math> r</math> vector. We can then find the location of the particle as we know  <math>r=r_{observation}-r_{particle}</math>
 <table border>
    <tr>
-     <td> <b>Step 1.</b> Find the magnitude of the Electric field:
+     <td>
-<math> F = Eq </math>
+<b>Step 1.</b> Find the electric field using <math>\vec{F} = q\vec{E}</math>.
-<math> = E * -2mC </math>
-<math> E = \frac{< -5.5e3 , -5.5e3, -5.5e3>}{-2mC}
+<math>\vec{E} = \frac{\vec{F}}{q}</math>
+<math> = \frac{\langle -5.5\times10^{3}, -5.5\times10^{3}, -5.5\times10^{3}\rangle}{-2\times10^{-3}}</math>
-= <2.75e6 , 2.75e6, 2.75e6> </math> N/C
+<math> = \langle 2.75\times10^{6},\, 2.75\times10^{6},\, 2.75\times10^{6}\rangle</math> N/C
- </td></tr>
+    </td>
+  </tr>
+  <tr>
+    <td>
+<b>Step 2.</b> Compute <math>\vec{r}</math> from the particle at the origin to the observation location.
+<math>\vec{r} = \langle 3.98,\,3.98,\,3.98\rangle\ \text{m}</math>
+Magnitude:
-    <tr><td><b>Step 2:</b> Find <math>\vec r_{obs} - \vec r_{particle} </math>.
+<math>|\vec{r}| = \sqrt{3.98^2 + 3.98^2 + 3.98^2}</math>
+<math>= \sqrt{47.52} \approx 6.89\ \text{m}</math>
-<math>\vec r = <3.98 , 3.98 , 3.98> m - <0 , 0 , 0> m = <3.98 , 3.98 , 3.98> m </math>
+Unit vector:
-To find <math>\vec r_{mag} </math>, find the magnitude of <math><3.98 , 3.98 , 3.98></math>
+<math>\hat{r} = \frac{\vec{r}}{|\vec{r}|}</math>
+    </td>
+  </tr>
-<math>\sqrt{3.98^2+3.98^2+3.98^2}=\sqrt{47.52}= 6.9</math>
+  <tr>
-  </td></tr>
+    <td>
+<b>Step 3.</b> Solve for the unknown charge using the point-charge field equation:
-    <td> '''Step 3:''' Find '''''q''''' by rearranging the equation for <math>E_{mag}</math>
+<math>E_{mag}=\frac{1}{4\pi\epsilon_0}\frac{|q|}{r^2}</math>
-<math> E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} </math>
+Rearranged:
-By rearranging this equation we get
+<math>|q| = (4\pi\epsilon_0)\,(r^2)\,E_{mag}</math>
-<math> q= {4 pi * \epsilon_0 } *{r^2}*E_{mag} </math>
+Using <math>E_{mag} = 2.75\times10^{6}</math> N/C and <math>r = 6.89</math> m:
-<math> q= {{1/(9e9)} *{6.9^{2}}*4.76e6} </math>
+<math>|q| = (8.99\times10^{-12})(6.89^2)(2.75\times10^{6})</math>
-<math> q= + 0.253 C </math></td>
+<math>|q| \approx 0.237\ \text{C}</math>
+Sign of the charge:
+The force on the negative test charge is **toward** the origin → the source must be **positive**.
+<b>Final Answer:</b>
+<math>q_{\text{origin}} \approx +0.24\ \text{C}</math>
+    </td>
+  </tr>
 </table border>
+====Common Mistakes====
+* **Using the wrong sign for q.**
+  Remember: if the force on a negative charge points toward the origin, the source must be positive.
+* **Forgetting that E and F point the same direction only for positive test charges.**
+  Since the test charge is −2 mC, is opposite the force direction.
+* **Mixing up <math>\vec{r}</math> and <math>|\vec{r}|</math>.**
+  One is a vector; the other is a scalar distance.
+* **Failing to use the magnitude of E when solving for |q|.**
+  The field equation uses only magnitudes, not vector components.
+* **Using an incorrect value of Coulomb’s constant.**
 ==Connectedness==
 ''1. How is this topic connected to something that you are interested in?''
-I think the topic is interesting because electric fields are inside the human body and we self-create these fields constantly. It's really cool to think about how your body might be responding and creating these fields continuously and what happens when the balances are thrown off by something (i.e. illness, injury).
+The topic is fascinating because electric fields not only exist within the human body but also in the realms of aerospace. It's captivating to think about the parallels between biological systems and aerospace systems, where electric field management is crucial for functions such as propulsion and navigation. Analyzing how bodies maintain and adapt their electric fields and applying this knowledge to aerospace engineering can lead to innovative approaches to energy management and system efficiency, particularly in the face of perturbations such as equipment failure or external environmental factors.
 ''2. How is it connected to your major?''
-I'm a business major, but I'm pre-med so it's interesting to think about point charges/electric fields in the macroscopic lens and how they can combine with other forces (magnetic --> electromagnetic forces) to affect your internal systems and processes that occur without you consciously thinking about them.
+As an aerospace engineer, my interest lies in the application of principles from various sciences, including biochemistry, to improve and innovate within the field of aviation and space exploration. Understanding the role of electric fields in cellular behavior provides insights into potential analogs in aerospace technology. For instance, similar to how cells adjust their electric fields for optimal function, aerospace systems must regulate their onboard electric fields for navigation, communication, and operational efficiency. Such interdisciplinary knowledge can be the foundation for advancements in aerospace materials and systems that are responsive and adaptive to their environments.
 ''3. Is there an interesting industrial application?''
-PEMF stands for pulsed electricmagnetic field, which is used by athletes during recovery or physical therapy. There is a difference in cell voltage between healthy cells and diseased cells. While healthy cells maintain a voltage around 70-100 mV, cells with illness have diminished voltage around 40mV. PEMF restores that optimal voltage in damaged cells. Through the utilization of low frequency pulsed electromagnetic fields at a high intensity, voltage in the damaged cells is increased. This stimulates cellular repair and recharges the body’s cells to optimize their performance.
+PEMF (Pulsed Electromagnetic Field) therapy's principle of restoring optimal voltage in damaged cells through electromagnetic fields has interesting parallels in aerospace engineering. For example, the management of electromagnetic fields is critical in spacecraft and aircraft to protect onboard electronics and enhance communication signals. The concept of PEMF can inspire the development of systems that can self-regulate and optimize electrical potential across different components of an aircraft or spacecraft, thereby enhancing performance and resilience. Such systems could prove vital in long-duration space missions, where human intervention is limited, and the machine's ability to self-heal and maintain operational integrity can be a game-changer.
-PEMF therapy creates a magnetic field, which increases the movement of ions and electrolytes in the tissues and fluids of the body. The magnetic field helps cells increase ATP production, which restores and / or maintains normal cellular function, speeding up the tissues healing process, repairing damaged tissue, improving circulation, and increasing cellular energy.
 ==History==
@@ Line 246: / Line 295: @@
 Charles de Coulomb was born in June 14, 1736 in central France. He spent much of his early life in the military and was placed in regions throughout the world. He only began to do scientific experiments out of curiously on his military expeditions. However, when controversy arrived with him and the French bureaucracy coupled with the French Revolution, Coulomb had to leave France and thus really began his scientific career.
 Between 1785 and 1791, de Coulomb wrote several key papers centered around multiple relations of electricity and magnetism. This helped him develop the principle known as Coulomb's Law, which confirmed that the force between two electrical charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. This is the same relationship that is seen in the electric field equation of a point charge.
+[[File:Benjamin-Franklin-Portrait.png]]
+''Benjamin Franklin''
+Benjamin Franklin (1706–1790) made several foundational contributions to the early understanding of electric charge. Although he did not write mathematical laws like Coulomb, his ideas directly shaped the concepts used in point-charge physics.
+Franklin introduced the naming system of positive and negative charge, which is still used today. He proposed that charge behaves like a conserved quantity that can move between objects—an essential idea behind treating charges as isolated point charges located at specific positions in space.
 == See also ==
@@ Line 267: / Line 323: @@
 Some more information:
-*http://hyperphysics.phy-astr.gsu.edu/hbase/electric/epoint.html
 *http://www.physics.umd.edu/courses/Phys260/agashe/S10/notes/lecture18.pdf
 *https://www.reliantphysicaltherapy.com/services/pulsed-electromagnetic-field-pemf
+*https://www.youtube.com/watch?v=HG9KxDZ-qwI&t=1s
+*https://www.youtube.com/watch?v=8GJf-Fj-qoI&t=3s
 ==References==

Point Charge: Difference between revisions

Latest revision as of 22:59, 23 November 2025

The Main Ideas

The Electric Field

A Mathematical Model

Electric Field Due to a Point Charge

Coulomb Force Law for Point Charges

Connection Between Electric Field and Force

Electric Field Superposition (Point Charges)

A Computational Model

A Computational Model 2

Examples

Simple

Middling

Difficult

Common Mistakes

Connectedness

History

See also

Further reading

External links

References

Navigation menu

Search