Lorentz Force: Difference between revisions
No edit summary |
|||
| (154 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:Headerlorentz.png|400px|thumb|right|Lorentz force diagram]] | |||
<h1><strong>Edited by Fiza Shaikh Fall 2020</strong></h1> | |||
==The Main Idea== | ==The Main Idea== | ||
The Lorentz force is the combined effect of the electric and magnetic force on a point charge/particle ''q'' due to the influence of electromagnetic fields. This particle is moving with a velocity ''v'' through an electrical field ''E'' and magnetic field ''B''. The Lorentz force can be generally represented as a combination of the previous forces on a point particle using this equation: | |||
<math> \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B}</math> | |||
Variations to this equation can help describe situations such as the magnetic force on a current-carrying wire, the force on a moving and charged particle, and the electromotive force. | |||
In most cases studied throughout college physics courses, the Lorentz Force on a particle is merely contributed by electric and magnetic forces, where other forces acting on the particle are considered negligible. Let's take a look at a simple situation that illustrates this subject in action. | |||
Taking two neutral currents in parallel, we notice something weird happen depending on the direction of the currents in relation to each other: | |||
[[File:meeds2.png]] | |||
Referencing the diagram above, we find that the parallel currents that run in the same direction undergo an attractive force. Alternatively, parallel currents that run in opposite directions undergo a repulsive force. Furthermore, experimental analysis prove that this resulting force is proportional to the currents (tripling the current in ''one'' of the wires triples the force, while tripling both of the currents produces a force 6x the original). With this in mind, it is clear that the force is proportional to the velocity of a moving charge and points in a direction perpendicular to the moving charge's velocity. This indicates that some kind of magnetic field ''B'' arises from moving charges, and this is a main concept of the Lorentz Force. | |||
== | ==Significance== | ||
The Lorentz force completes the picture that Maxwell's equations paint. Maxwell's equations describe how charged particles and electrical currents or even moving charged particles create and contribute to electric and magnetic fields. The Lorentz force takes Maxwell's equations and completes the picture by describing the force that acts on a moving charge ''q'' in the presence of an electromagnetic field(s). Lorentz law plays a major role in the behavior of charged particles. One is how the particle itself responds to being subject to Lorentz law. Two is how the electric ''E'' and magnetic ''B'' fields by currents and charges are generated. | |||
Generally, the Lorentz force falls short of being the general solution and cannot describe the collective behavior of charged particles conceptually or mathematically. In materials, one must use more complex transport equations to determine how charges respond within the space they are inhabiting. | |||
==A Mathematical Model== | |||
The electromagnetic force ''F'' on a charged particle, the Lorentz force (named after the Dutch physicist [http://www.physicsbook.gatech.edu/Hendrik_Lorentz Hendrik A. Lorentz]) is given by: | |||
<math> \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B}</math> | |||
where '''<math>q\vec{E}</math>''' is the electric force contributed by an external electric field and ''' <math>q\vec{v} ⨯ \vec{B}</math>''' is the magnetic force contributed by an external magnetic field. As many applications involve vectors, it is valuable to recognize the resulting directions of '''<math>q\vec{E}</math>''' and ''' <math>q\vec{v} ⨯ \vec{B}</math>''' in relation to the particle's charge and velocity within the environment of applied electric/magnetic fields. The resulting electric force vector will always be towards or opposite to the applied electric field, depending on the sign of the charge. For example, an electron undergoing an electric field in the +x direction will receive an electric force in the -x direction. The magnetic force on the particle, however, has a direction perpendicular to both the velocity ''v'' of the particle and the magnetic field ''B'', and has a value proportional to ''q'' and to the magnitude of the vector cross product ''' <math>q\vec{v} ⨯ \vec{B}</math>'''. More specifically, the magnitude of the magnetic force equals ''qvBsinθ'' where ''θ'' is the angle between ''v'' and ''B''. | |||
====Motion of a Charged Particle in a Uniform Magnetic Field==== | |||
A noteworthy result of the Lorentz force is the motion of a charged particle within a uniform magnetic field as the angle between ''v'' and ''B'' varies. If a scenario presents a charged particle with a velocity vector ''v'' perpendicular to the applied magnetic field ''B'' (i.e. θ = 90°), the particle will follow a circular trajectory. The radius of this trajectory can easily be calculated: | |||
<math> \vec{F}_{Mag} = \vec{F}_{Centripetal}</math> | |||
<math> qvB = mv^2/R </math> | |||
<math> R = mv/qB </math> | |||
Suppose that for the following example, a charge is shot into a region filled with a uniform magnetic field coming out of the page: | |||
[[File:Meeds1.png]] | |||
At every instant, the external magnetic field ''B'' points out of the page and thus invokes a magnetic force on the particle perpendicular to the particle's velocity - the force needed to create circular motion. The radius ''R'' can be calculated from the equation above. In addition, it's worth noting that the particle's charge will determine where the particle veers. If the particle were positively charged, the magnetic force would cause the particle to veer downward (due to right hand rule), and vice-versa if negatively charged. | |||
In the case that θ is less than 90°, the particle's trajectory will orbit a helix path with a central axis parallel to the field lines. | |||
If θ is zero, that is, the magnetic field is in the same direction as the particle's velocity, the particle will experience no magnetic force and continue to move normally along the field lines. | |||
==A Computational Model== | |||
[https://trinket.io/embed/glowscript/43e56e9c64 Here is a visualization] on VPython of a negatively charged particle moving through a constant electric and magnetic field: | |||
[[File:Lorentzdiagram.png]] | |||
Initially, a negatively charged particle is traveling with initial velocity in the -z direction. There is a constant electric field ''E'' in the -x direction and a constant magnetic field ''B'' in the +y direction. The magnetic force on the negatively charged particle is equal to <math> q\vec{v} ⨯ \vec{B}</math>, or the charge of the particle times the cross product of the particle’s velocity and the magnetic field it travels through. The electric force on the particle is equal to <math> q\vec{E} </math>, or the charge of the particle times the electric field that the particle travels through. Since the magnetic force on the particle is related to the particle’s velocity ''v'', the magnetic force changes as the the particle’s velocity changes. Conversely, the electric force on the particle is constant. Since the Magnetic force is variable, the Lorentz Force on the particle, or the net force due to magnetic and electric forces on the particle (<math> \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B}</math>) is also variable, and the particle's velocity changes. | |||
==Example Problems== | |||
===Simple=== | ===Simple=== | ||
The | The electric force on a certain particle is <100,-600,300> N and the magnetic force is <-600,400,0> N. Find the Lorentz force. | ||
'''Solution: Lorentz force = <-500,-200,300> N''' | |||
[[File:Soln2.PNG]] | |||
=== | ===Intermediate=== | ||
The magnetic force on a proton is 100 N at an angle 30 degrees down from the +x axis. The electric force on the proton is 100 N at an angle 30 degrees up from the +z axis. What is the magnitude of the Lorentz Force on the proton? | |||
'''Solution: Lorentz force = 122.5 N''' | |||
[[File:Soln1.PNG]] | |||
===Difficult=== | ===Difficult=== | ||
An electron is traveling with a constant velocity of <0.75c, 0, 0>. You measure the magnetic field to be <0.4, 0.3, 0.5>T everywhere. What is the electric field? | |||
'''Solution: E = <0, 1.13e8, -6.75e7> N/C ''' | |||
Since the electron is traveling at constant velocity, the net force must be zero. Thus, the magnetic field must equal the electric field, or <math> q\vec{v} ⨯ \vec{B}= q\vec{E} </math>. The charge on both sides cancels out to give <math> \vec{v} ⨯ \vec{B}= \vec{E} </math>. Calculating | |||
<math> q\vec{v} ⨯ \vec{B}</math> = <0, -1.13e8, 6.75e7>, so the electric field must point in the opposite direction. | |||
==Connectedness== | |||
1. Speakers use the Lorentz force of an electromagnet to move a cone that creates sound waves in the air. When current flows through the wires in the electromagnetic in different quantities, the speakers move in unique ways to produce the different sounds that we recognize. Amplifiers for electric guitars and basses work in the same way. | |||
2. In today's evolving world, one area of particular interest is sustainable and renewable energy. Wind turbines and hydropower plants work by harnessing the kinetic energy of wind or water and using it to induce an electrical current. The turbines rotate and move a permanent magnet that induces a current in an electromagnet placed inside of the magnet, which is shaped like a hollow cylinder. The induced current is then carried via wires to external sources to provide energy. | |||
== | 3. Several industries manufacture products that induce current using the Lorentz Force. For example, electric guitars and basses work by magnetizing the strings and relying on the Lorentz force to create a current in pickups that is then transmitted to an amplifier. Pickups are small electromagnet coils surrounding a magnet that are placed beneath the strings. The strings become magnetized because of the magnet inside the pickup. When they are played and vibrate, they induce current in the electromagnet. The Lorentz force causes the strings to exert forces that move mobile charges and induce the current. The current is then increased through a potentiometer and sent to an amplifier through a cable. In addition, charged particle accelerators like cyclotrons make use of the circular orbit particles experience when ''v'' and ''B'' are perpendicular to each other. For each revolution, a carefully timed electric field offers additional kinetic energy to cause the particles to move in increasingly-larger orbits until the desired energy level is met. These particles are known to be extracted and used in a number of ways, from basic studies of the properties of matter to the medical treatment of cancer. | ||
==Applications== | |||
Specific applications of the Lorentz force have enabled some of the most significant scientific experimentation to date. | |||
It is known that when the angle between ''v'' and ''B'' is 90 degrees, there is no magnetic force on the particle which continues to move unaffected along the field lines. Cyclotrons and other charged particle accelerators make use of this fact and that particles move in circular orbit when ''v'' and ''B'' are perpendicular with respect to each other (therefore their cross product is equal to 0). With each revolution, these particles gain additional kinetic energy from the electric field which therefore increases orbit. Once reaching the desired energy level, they can be extracted and used in various ways from studies on subatomic particles to even medical treatments for diseases like cancer. | |||
Scientists at the European Organization for Nuclear Research(CERN), the largest organization for particle research, take advantage of the Lorentz force in their collider experiments[4]. | |||
==History== | ==History== | ||
[[[[File:Hendrik Antoon Lorentz.jpg|thumb|right|Hendrik Antoon Lorentz]] | |||
The Lorentz Force is named after Hendrik Lorentz, who derived the formula in the late 19th century following a previous derivation by [[Oliver Heaviside]] in 1889. However, scientists had tried to find formulas for one electromagnetic force for over a hundred years before.Some scientists such as [[Henry Cavendish]] argued that the magnetic poles of an object could create an electric force on a particle that obeys an inverse-square law. However, the experimental proof was not enough to definitively publish. In 1784, [[Charles de Coulomb]], using a torsion balance, was able to definitively show through experiment that this was true. After [[Hans Christian Ørsted]] discovered that a magnetic needle is acted on by a voltaic current, [[Andre Marie Ampere]] derived a new formula for the angular dependence of the force between two current elements. However, the force was still given in terms of the properties of the objects involved and the distances between, not in terms of electric and magnetic fields or forces. | |||
[[Michael Faraday]] introduced modern ideas of magnetic and electric fields, including their interactions and relations with each other, later to be given full mathematical description by [[William Thomson (Lord Kelvin)]] and [[James Maxwell]]. From a modern perspective it is possible to identify in Maxwell's 1865 formulation of his field equations a form of the Lorentz force equation in relation to electric currents, however, it was not initially evident how his equations related to the forces on moving charged objects. [[J.J. Thomson]] was the first to attempt to derive from Maxwell's field equations the electromagnetic forces on a moving charged object in terms of the object's properties and external fields. Interested in determining the electromagnetic behavior of the charged particles in cathode rays, Thomson published a paper in 1881 wherein he gave the force on the particles due to an external magnetic field as <math>\vec{F} = q\vec{E} + \frac{q}{2}\vec{v} ⨯ \vec{B}</math>. Finally, Heaviside and later Lorentz were able to combine the information into the currently accepted Lorentz Force equation. | |||
== See also == | == See also == | ||
The [[Hall Effect]] is a special case in which the magnetic and electric forces on a particle or object cancel out, meaning that there is zero net force. Solving these problems involves setting the two forces equal to each other and using given information to find values for <math>\vec{B}</math>, <math>\vec{v}</math>, or <math>\vec{E}</math>. | |||
[https://www.youtube.com/watch?v=8QWB8IfNoIs This video] demonstrates a few everyday applications and examples of the Lorentz Force. | |||
===Further reading=== | ===Further reading=== | ||
[[Hall Effect]] | |||
*http://hyperphysics.phy-astr.gsu.edu/HBASE/hframe.html | |||
*http://www.ittc.ku.edu/~jstiles/220/handouts/section%203_6%20The%20Lorentz%20Force%20Law%20package.pdf | |||
===External links=== | ===External links=== | ||
[1]*http://jnaudin.free.fr/lifters/lorentz/ | |||
[2]*https://nationalmaglab.org/education/magnet-academy/watchplay/interactive/lorentz-force | |||
[3]*http://web.mit.edu/sahughes/www/8.022/lec10.pdf | |||
[4]*https://www.lhc-closer.es/taking_a_closer_look_at_lhc/0.lorentz_force | |||
==References== | ==References== | ||
*Feynman, Richard Phillips; Leighton, Robert B.; Sands, Matthew L. (2006). The Feynman lectures on physics (3 vol.). Pearson / Addison-Wesley. ISBN 0-8053-9047-2.: volume 2. | |||
*Jackson, John David (1999). Classical electrodynamics (3rd ed.). New York, [NY.]: Wiley. ISBN 0-471-30932-X. | |||
*Serway, Raymond A.; Jewett, John W., Jr. (2004). Physics for scientists and engineers, with modern physics. Belmont, [CA.]: Thomson Brooks/Cole. ISBN 0-534-40846-X. | |||
*Hughs, Scott. “Magnetic Force; Magnetic Fields; Ampere's Law.” MIT.edu. Magnetic Force; Magnetic Fields; Ampere's Law, 29 Nov. 2017, Boston, MIT, Magnetic Force; Magnetic Fields; Ampere's Law. | |||
[[Category:Which Category did you place this in?]] | [[Category:Which Category did you place this in?]] | ||
Latest revision as of 17:59, 13 November 2020
Edited by Fiza Shaikh Fall 2020
The Main Idea
The Lorentz force is the combined effect of the electric and magnetic force on a point charge/particle q due to the influence of electromagnetic fields. This particle is moving with a velocity v through an electrical field E and magnetic field B. The Lorentz force can be generally represented as a combination of the previous forces on a point particle using this equation:
[math]\displaystyle{ \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} }[/math]
Variations to this equation can help describe situations such as the magnetic force on a current-carrying wire, the force on a moving and charged particle, and the electromotive force.
In most cases studied throughout college physics courses, the Lorentz Force on a particle is merely contributed by electric and magnetic forces, where other forces acting on the particle are considered negligible. Let's take a look at a simple situation that illustrates this subject in action.
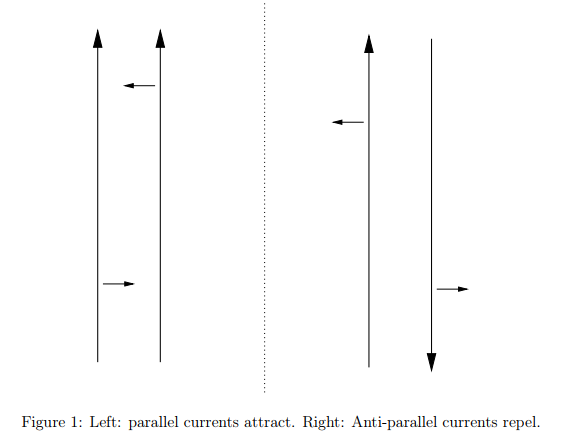
Taking two neutral currents in parallel, we notice something weird happen depending on the direction of the currents in relation to each other:
Referencing the diagram above, we find that the parallel currents that run in the same direction undergo an attractive force. Alternatively, parallel currents that run in opposite directions undergo a repulsive force. Furthermore, experimental analysis prove that this resulting force is proportional to the currents (tripling the current in one of the wires triples the force, while tripling both of the currents produces a force 6x the original). With this in mind, it is clear that the force is proportional to the velocity of a moving charge and points in a direction perpendicular to the moving charge's velocity. This indicates that some kind of magnetic field B arises from moving charges, and this is a main concept of the Lorentz Force.
Significance
The Lorentz force completes the picture that Maxwell's equations paint. Maxwell's equations describe how charged particles and electrical currents or even moving charged particles create and contribute to electric and magnetic fields. The Lorentz force takes Maxwell's equations and completes the picture by describing the force that acts on a moving charge q in the presence of an electromagnetic field(s). Lorentz law plays a major role in the behavior of charged particles. One is how the particle itself responds to being subject to Lorentz law. Two is how the electric E and magnetic B fields by currents and charges are generated.
Generally, the Lorentz force falls short of being the general solution and cannot describe the collective behavior of charged particles conceptually or mathematically. In materials, one must use more complex transport equations to determine how charges respond within the space they are inhabiting.
A Mathematical Model
The electromagnetic force F on a charged particle, the Lorentz force (named after the Dutch physicist Hendrik A. Lorentz) is given by:
[math]\displaystyle{ \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} }[/math]
where [math]\displaystyle{ q\vec{E} }[/math] is the electric force contributed by an external electric field and [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math] is the magnetic force contributed by an external magnetic field. As many applications involve vectors, it is valuable to recognize the resulting directions of [math]\displaystyle{ q\vec{E} }[/math] and [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math] in relation to the particle's charge and velocity within the environment of applied electric/magnetic fields. The resulting electric force vector will always be towards or opposite to the applied electric field, depending on the sign of the charge. For example, an electron undergoing an electric field in the +x direction will receive an electric force in the -x direction. The magnetic force on the particle, however, has a direction perpendicular to both the velocity v of the particle and the magnetic field B, and has a value proportional to q and to the magnitude of the vector cross product [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math]. More specifically, the magnitude of the magnetic force equals qvBsinθ where θ is the angle between v and B.
Motion of a Charged Particle in a Uniform Magnetic Field
A noteworthy result of the Lorentz force is the motion of a charged particle within a uniform magnetic field as the angle between v and B varies. If a scenario presents a charged particle with a velocity vector v perpendicular to the applied magnetic field B (i.e. θ = 90°), the particle will follow a circular trajectory. The radius of this trajectory can easily be calculated:
[math]\displaystyle{ \vec{F}_{Mag} = \vec{F}_{Centripetal} }[/math]
[math]\displaystyle{ qvB = mv^2/R }[/math]
[math]\displaystyle{ R = mv/qB }[/math]
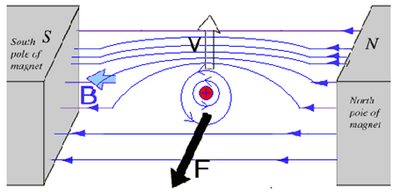
Suppose that for the following example, a charge is shot into a region filled with a uniform magnetic field coming out of the page:
At every instant, the external magnetic field B points out of the page and thus invokes a magnetic force on the particle perpendicular to the particle's velocity - the force needed to create circular motion. The radius R can be calculated from the equation above. In addition, it's worth noting that the particle's charge will determine where the particle veers. If the particle were positively charged, the magnetic force would cause the particle to veer downward (due to right hand rule), and vice-versa if negatively charged.
In the case that θ is less than 90°, the particle's trajectory will orbit a helix path with a central axis parallel to the field lines.
If θ is zero, that is, the magnetic field is in the same direction as the particle's velocity, the particle will experience no magnetic force and continue to move normally along the field lines.
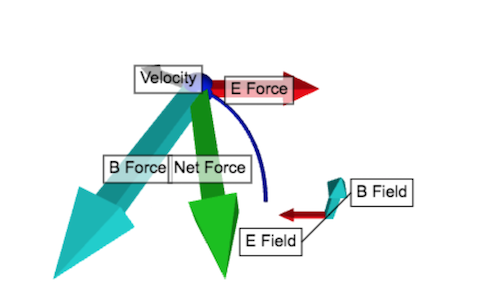
A Computational Model
Here is a visualization on VPython of a negatively charged particle moving through a constant electric and magnetic field:
Initially, a negatively charged particle is traveling with initial velocity in the -z direction. There is a constant electric field E in the -x direction and a constant magnetic field B in the +y direction. The magnetic force on the negatively charged particle is equal to [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math], or the charge of the particle times the cross product of the particle’s velocity and the magnetic field it travels through. The electric force on the particle is equal to [math]\displaystyle{ q\vec{E} }[/math], or the charge of the particle times the electric field that the particle travels through. Since the magnetic force on the particle is related to the particle’s velocity v, the magnetic force changes as the the particle’s velocity changes. Conversely, the electric force on the particle is constant. Since the Magnetic force is variable, the Lorentz Force on the particle, or the net force due to magnetic and electric forces on the particle ([math]\displaystyle{ \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} }[/math]) is also variable, and the particle's velocity changes.
Example Problems
Simple
The electric force on a certain particle is <100,-600,300> N and the magnetic force is <-600,400,0> N. Find the Lorentz force.
Solution: Lorentz force = <-500,-200,300> N

Intermediate
The magnetic force on a proton is 100 N at an angle 30 degrees down from the +x axis. The electric force on the proton is 100 N at an angle 30 degrees up from the +z axis. What is the magnitude of the Lorentz Force on the proton?
Solution: Lorentz force = 122.5 N
Difficult
An electron is traveling with a constant velocity of <0.75c, 0, 0>. You measure the magnetic field to be <0.4, 0.3, 0.5>T everywhere. What is the electric field?
Solution: E = <0, 1.13e8, -6.75e7> N/C
Since the electron is traveling at constant velocity, the net force must be zero. Thus, the magnetic field must equal the electric field, or [math]\displaystyle{ q\vec{v} ⨯ \vec{B}= q\vec{E} }[/math]. The charge on both sides cancels out to give [math]\displaystyle{ \vec{v} ⨯ \vec{B}= \vec{E} }[/math]. Calculating [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math] = <0, -1.13e8, 6.75e7>, so the electric field must point in the opposite direction.
Connectedness
1. Speakers use the Lorentz force of an electromagnet to move a cone that creates sound waves in the air. When current flows through the wires in the electromagnetic in different quantities, the speakers move in unique ways to produce the different sounds that we recognize. Amplifiers for electric guitars and basses work in the same way.
2. In today's evolving world, one area of particular interest is sustainable and renewable energy. Wind turbines and hydropower plants work by harnessing the kinetic energy of wind or water and using it to induce an electrical current. The turbines rotate and move a permanent magnet that induces a current in an electromagnet placed inside of the magnet, which is shaped like a hollow cylinder. The induced current is then carried via wires to external sources to provide energy.
3. Several industries manufacture products that induce current using the Lorentz Force. For example, electric guitars and basses work by magnetizing the strings and relying on the Lorentz force to create a current in pickups that is then transmitted to an amplifier. Pickups are small electromagnet coils surrounding a magnet that are placed beneath the strings. The strings become magnetized because of the magnet inside the pickup. When they are played and vibrate, they induce current in the electromagnet. The Lorentz force causes the strings to exert forces that move mobile charges and induce the current. The current is then increased through a potentiometer and sent to an amplifier through a cable. In addition, charged particle accelerators like cyclotrons make use of the circular orbit particles experience when v and B are perpendicular to each other. For each revolution, a carefully timed electric field offers additional kinetic energy to cause the particles to move in increasingly-larger orbits until the desired energy level is met. These particles are known to be extracted and used in a number of ways, from basic studies of the properties of matter to the medical treatment of cancer.
Applications
Specific applications of the Lorentz force have enabled some of the most significant scientific experimentation to date.
It is known that when the angle between v and B is 90 degrees, there is no magnetic force on the particle which continues to move unaffected along the field lines. Cyclotrons and other charged particle accelerators make use of this fact and that particles move in circular orbit when v and B are perpendicular with respect to each other (therefore their cross product is equal to 0). With each revolution, these particles gain additional kinetic energy from the electric field which therefore increases orbit. Once reaching the desired energy level, they can be extracted and used in various ways from studies on subatomic particles to even medical treatments for diseases like cancer.
Scientists at the European Organization for Nuclear Research(CERN), the largest organization for particle research, take advantage of the Lorentz force in their collider experiments[4].
History
[[

The Lorentz Force is named after Hendrik Lorentz, who derived the formula in the late 19th century following a previous derivation by Oliver Heaviside in 1889. However, scientists had tried to find formulas for one electromagnetic force for over a hundred years before.Some scientists such as Henry Cavendish argued that the magnetic poles of an object could create an electric force on a particle that obeys an inverse-square law. However, the experimental proof was not enough to definitively publish. In 1784, Charles de Coulomb, using a torsion balance, was able to definitively show through experiment that this was true. After Hans Christian Ørsted discovered that a magnetic needle is acted on by a voltaic current, Andre Marie Ampere derived a new formula for the angular dependence of the force between two current elements. However, the force was still given in terms of the properties of the objects involved and the distances between, not in terms of electric and magnetic fields or forces.
Michael Faraday introduced modern ideas of magnetic and electric fields, including their interactions and relations with each other, later to be given full mathematical description by William Thomson (Lord Kelvin) and James Maxwell. From a modern perspective it is possible to identify in Maxwell's 1865 formulation of his field equations a form of the Lorentz force equation in relation to electric currents, however, it was not initially evident how his equations related to the forces on moving charged objects. J.J. Thomson was the first to attempt to derive from Maxwell's field equations the electromagnetic forces on a moving charged object in terms of the object's properties and external fields. Interested in determining the electromagnetic behavior of the charged particles in cathode rays, Thomson published a paper in 1881 wherein he gave the force on the particles due to an external magnetic field as [math]\displaystyle{ \vec{F} = q\vec{E} + \frac{q}{2}\vec{v} ⨯ \vec{B} }[/math]. Finally, Heaviside and later Lorentz were able to combine the information into the currently accepted Lorentz Force equation.
See also
The Hall Effect is a special case in which the magnetic and electric forces on a particle or object cancel out, meaning that there is zero net force. Solving these problems involves setting the two forces equal to each other and using given information to find values for [math]\displaystyle{ \vec{B} }[/math], [math]\displaystyle{ \vec{v} }[/math], or [math]\displaystyle{ \vec{E} }[/math].
This video demonstrates a few everyday applications and examples of the Lorentz Force.
Further reading
- http://hyperphysics.phy-astr.gsu.edu/HBASE/hframe.html
- http://www.ittc.ku.edu/~jstiles/220/handouts/section%203_6%20The%20Lorentz%20Force%20Law%20package.pdf
External links
[1]*http://jnaudin.free.fr/lifters/lorentz/ [2]*https://nationalmaglab.org/education/magnet-academy/watchplay/interactive/lorentz-force [3]*http://web.mit.edu/sahughes/www/8.022/lec10.pdf [4]*https://www.lhc-closer.es/taking_a_closer_look_at_lhc/0.lorentz_force
References
- Feynman, Richard Phillips; Leighton, Robert B.; Sands, Matthew L. (2006). The Feynman lectures on physics (3 vol.). Pearson / Addison-Wesley. ISBN 0-8053-9047-2.: volume 2.
- Jackson, John David (1999). Classical electrodynamics (3rd ed.). New York, [NY.]: Wiley. ISBN 0-471-30932-X.
- Serway, Raymond A.; Jewett, John W., Jr. (2004). Physics for scientists and engineers, with modern physics. Belmont, [CA.]: Thomson Brooks/Cole. ISBN 0-534-40846-X.
- Hughs, Scott. “Magnetic Force; Magnetic Fields; Ampere's Law.” MIT.edu. Magnetic Force; Magnetic Fields; Ampere's Law, 29 Nov. 2017, Boston, MIT, Magnetic Force; Magnetic Fields; Ampere's Law.