Hall Effect

Edited by Adeline Boswell Fall 2019, Edited by Alayna Baker Spring 2020

The Hall Effect is the electric polarization of a block or slab of metal that occurs when a current is run through it while it is subject to a magnetic field perpendicular to the current.

The Main Idea

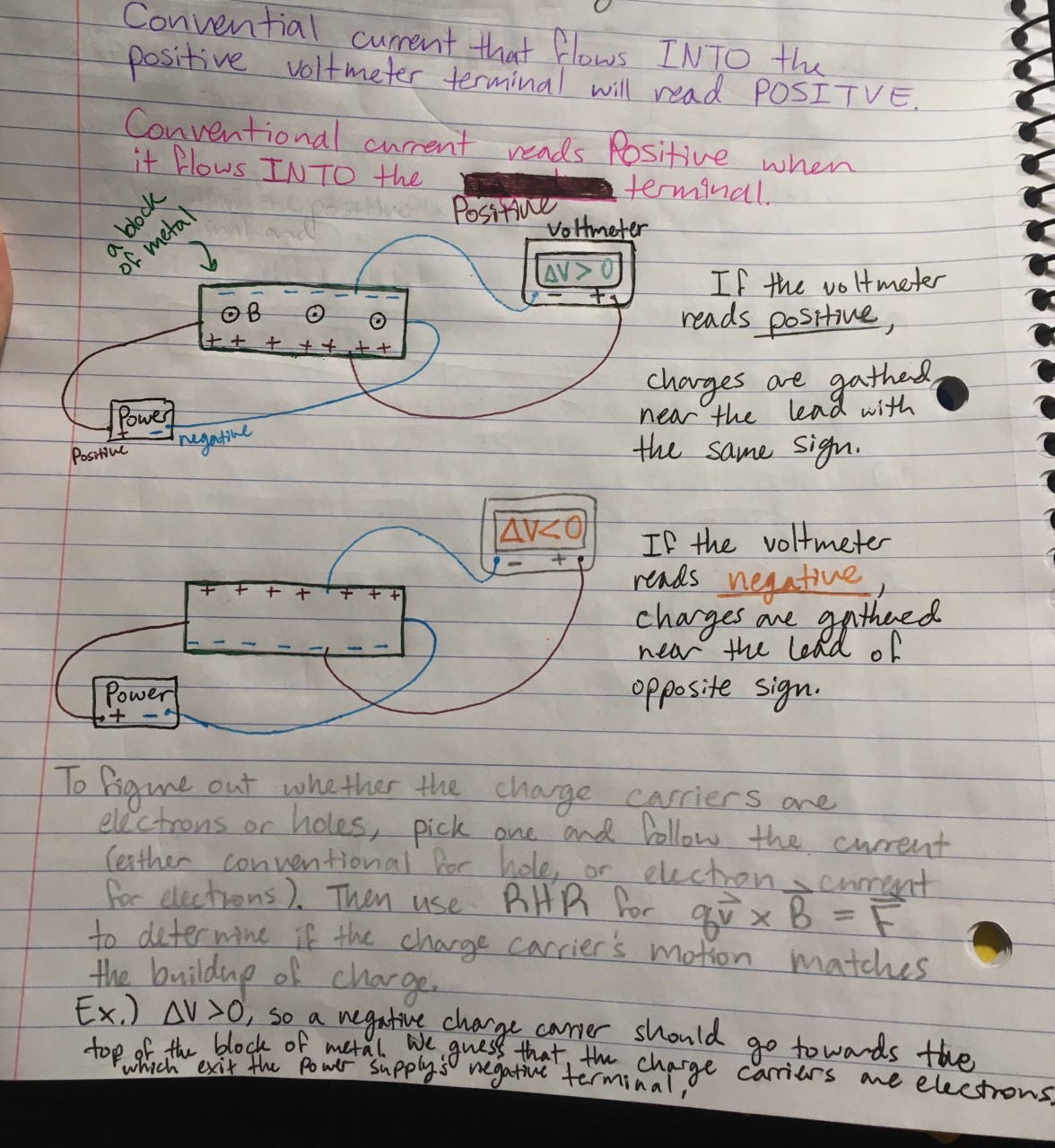
When a mobile charge, either positive or negative, flows through a metal block and is influenced by a magnetic field, the magnetic force on the charges force them to begin concentrating on one side of the block. Thus the block polarizes and has negative charges on one side and positive on the other in order to remain neutral. This grouping of positive charges in one part of the block and negative charges in another part of the block creates an electric field and thus an electric force equal on magnitude to the magnetic force that causes the initial polarization, but opposite in direction. The magnetic and electric forces cancel each other out and after some time, the charges flow normally through the block and do not group on one side or the other of the block. This perpendicular electric field also creates a potential difference known as the "Hall Voltage."

Part 1: Normal circuit (No Magnetic Field Yet)

(For simplicity, the mobile charges in this example have already been determined to be negatively charged electrons. This will not always be the case and it should not be assumed that the mobile charges are electrons)

Mobile electrons flow through a wire due to a parallel electric field inside the wire. This electric field is caused by an energy source, most commonly a battery. The parallel electric field flows from an area of high potential (i.e. the positive end of the battery) to an area of low potential (i.e. the negative end of the battery). This is the same direction as the conventional current. Since electrons are negatively charged, they flow in the opposite direction of the parallel electric field.

Part 2: Initial Transient State (Magnetic Field Present)

Mobile electrons are subjected to a magnetic field perpendicular to their motion as they flow through the wire. This results in the mobile charges being forced onto one side of the block by the magnetic force. This grouping of mobile charges on one side of the block creates an electric force. As time passes, more mobile charges are deposited on the side of the block and the electric force increases in magnitude.

Part 3: Steady State (Magnetic Field Still Present, but abated)

Over time massive quantities of charges are concentrated on one side of the block. As the charges build up, they will begin to create a charged area on one surface of the conductor. The charged surface will create an electric force to oppose the magnetic force that is pushing new electrons onto this charged surface. This opposing electric force is called the transverse electric force. When enough mobile charges have collected, their combined transverse electric force will be equal in magnitude to the magnetic force that is holding them. At this point, there is no net vertical force pushing more electrons against the surface of the conductor and these electrons will flow normally again, as they would if there was no magnetic field present. This is called the steady state.

A Mathematical Model

Part 1: Normal circuit (No Magnetic Field Yet)

[math]\displaystyle{ F_{electric, parallel} = qE_{parallel} }[/math]

Where q is the electric charge of the mobile charge. As F and E are vectors, a negative charge results in an electric force in the opposite direction of the electric field.

Part 2: Initial Transient State (Magnetic Field Present)

[math]\displaystyle{ F_{magnetic} = q(v\; Χ \;B) }[/math]

Where v is the velocity of the mobile charge and B is the magnetic field. For help calculating the cross product, including an example using the Hall Effect, see Right-Hand_Rule. REMEMBER, the mobile charge will move in the opposite direction of the cross product if it is negative, similar to how it behaves in an electric field.

Part 3: Steady State (Magnetic Field Still Present, but abated)

[math]\displaystyle{ F_{electric, perpendicular} = qE_{perpendicular} }[/math]

[math]\displaystyle{ |F_{electric, perpendicular}| = |F_{magnetic}| }[/math]

Computational Model

In this diagram, it is assumed the charge carrier is a negatively charged electron. THIS IS NOT A SAFE ASSUMPTION on a real question, experiment, or exam but was done for the purpose of simplifying explanations.

Part 1: Normal circuit (No Magnetic Field Yet)

In this diagram a solid conductive metal block is connected to two ends of a battery by wires. At this time there is no magnetic field present and electrons flow through the block in a straight line from wire to wire without interference or interruption.

Part 2: Initial Transient State (Magnetic Field Present)

In this diagram the circles containing x's represent a magnetic field (NOT a magnetic force) into the page. When the electrons begin to move across the block their initial velocity interacts with the magnetic field to create a magnetic force downward. This causes electrons to begin pooling on the bottom face of the slab. This polarizes the block and creates a vertical potential difference across the block. It also creates an electric force that opposes the magnetic force, but in this state it is smaller than the magnetic force, resulting in continued pooling of electrons.

Part 3: Steady State (Magnetic Field Still Present, but abated)

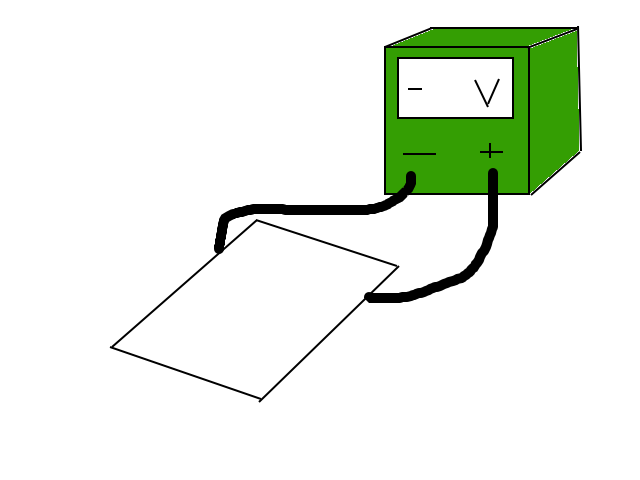
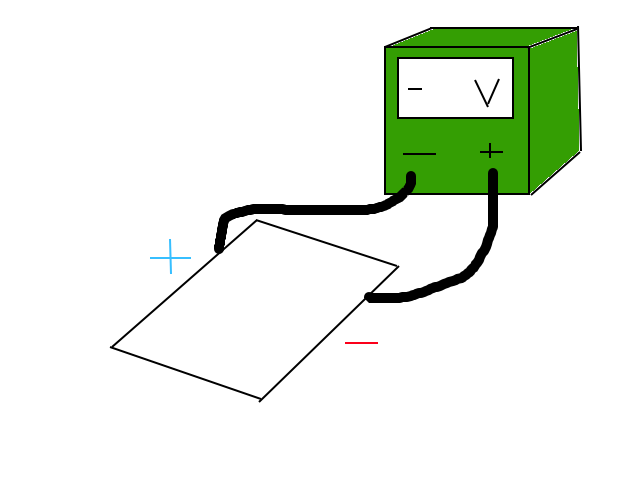
As time passes eventually sufficient quantities of electrons build up to create an electric force equal in magnitude to the magnetic force but opposite in direction. This allows the electrons to continue flow across the block as they did in part 1, however now the vertical voltage difference which was created in part 2 is not only still present but also at its maximum value. Most practice and exam problems will involve either the calculation or orientation of this voltage difference. It's important to remember that a voltmeter will have a positive reading if the positive node is connected to the end of the block which is positively charged and vice versa.

Examples

Simple

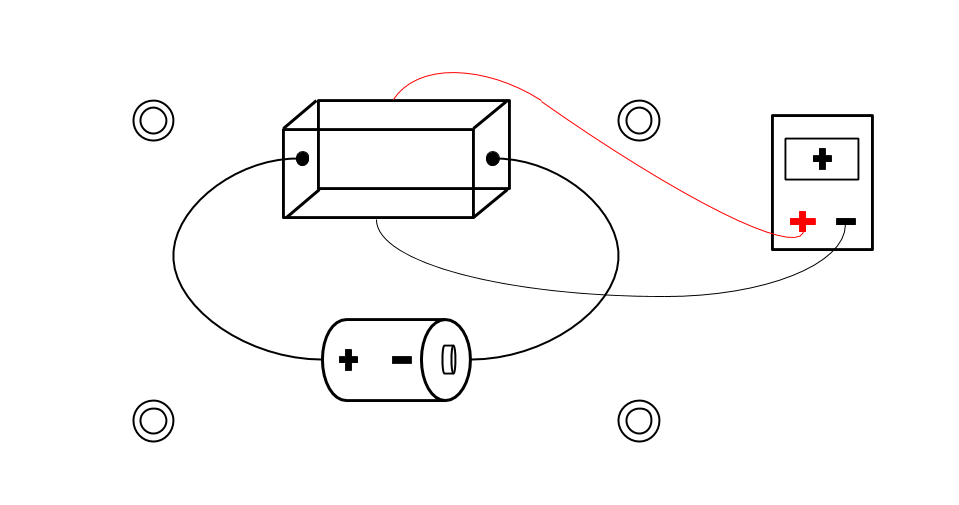
A metal block is connected to a battery by two wires. Conventional current flows clockwise and the mobile charge in the block is positive. The block also experiences a magnetic field out of the page denoted by concentric circles. The block is also connected to a voltmeter. The positive end of the voltmeter is connected to the bottom of the block and the negative end of the voltmeter is connected to the top of the block. See attached photo for a diagram. What sign will the voltmeter display?

Click for Solution

In this case, since magnetic force is q(v X B) and we know the charges are positive and thus follow the conventional current which moves across the block from left to right, the magnetic force points up. This means that the mobile charges (positive) will be pushed towards the bottom of the block. Remember: a voltmeter will have a positive reading if the positive end is connected to the positively charged side of the block. In this case, the bottom of the block is positively charged and the positive end of the voltmeter is connected there. The voltmeter will have a positive reading.

A battery and metal block are connected by 2 wires. Conventional current flows clockwise. A magnetic field points out of the page, denoted by concentric circles. A voltmeter is attached to the block with its positive lead at the top of the block and its negative lead at the bottom of the block. The voltmeter has a positive reading. What sign does the mobile charge have?

Click for Solution

From the voltmeter reading we can deduce that the top of the block is positively charged and the bottom negatively charged. Thus, we check if positive mobile charge carriers satisfy this requirement. A positive charge moves with the conventional current, which in this case is from left to right, meaning its velocity would be in the positive x direction. When taking the cross product of the charge's velocity and the magnetic field (out of the page) we get a magnetic force pointing downward, thus meaning the positive charges would be forced downward as well. This is in conflict with the positive voltmeter reading and thus cannot be true. Next we check if negative charge carriers agree with the voltmeter readings. A negatively charged mobile charge carrier moves counter to the conventional current, in this case meaning it moves across the block from right to left resulting in a velocity in the negative x direction. When we take the cross product of this velocity and the magnetic field out of the page multiplied by the charge of the carrier we get a magnetic force pointing downwards (using F = q(v X B). This would result in the block's bottom being negatively charged and the top being positively charged. This result agrees with the given voltmeter reading. The mobile charge carriers are negative.

Middling

[math]\displaystyle{ B = 1.8 T }[/math] out of the page (denoted by concentric circles)

[math]\displaystyle{ n = 7*10^{25} /m^3 }[/math]

[math]\displaystyle{ u = 3*10^{-5} }[/math]

1. What does reading does the voltmeter display (both magnitude and sign)?
2. What does reading does the Ammeter display(both magnitude and sign?

Click for Solution to #1

Step 1 Find [math]\displaystyle{ E_{Hall} }[/math]

[math]\displaystyle{ ΣF_y = q(v\; Χ \;B) + q|E_{Hall}| }[/math]

[math]\displaystyle{ 0 = q(v\; Χ \;B) + q|E_{Hall}| }[/math]

[math]\displaystyle{ q(v\; Χ \;B) = q|E_{Hall}| }[/math]

[math]\displaystyle{ |E_{Hall}| = (v\; Χ \;B) }[/math]

[math]\displaystyle{ |E_{Hall}| = |v| * |B| }[/math]

Step 2 Find v

[math]\displaystyle{ I = q*n*A*v }[/math]

[math]\displaystyle{ v = \frac{I}{q*n*A} }[/math]

Step 3 Substitute v into our formula for [math]\displaystyle{ E_{Hall} }[/math]

[math]\displaystyle{ |E_{Hall}| = \frac{I * |B|}{q*n*A} }[/math]

Step 4

[math]\displaystyle{ σ = q*n*u }[/math]

Step 5

[math]\displaystyle{ R = \frac{L}{σA} }[/math]

Step 6 Substitute σ

[math]\displaystyle{ R = \frac{L}{q*n*u*A} }[/math]

Step 7

[math]\displaystyle{ Emf = I*R }[/math]

Step 8 Substitute R

[math]\displaystyle{ Emf = \frac{I*L}{q*n*u*A} }[/math]

Step 9 Solve for I

[math]\displaystyle{ I = \frac{Emf*q*n*u*A}{L} }[/math]

Step 10 Substitute I in our formula for [math]\displaystyle{ E_{Hall} }[/math]

[math]\displaystyle{ |E_{Hall}| = \frac{Emf * u * |B|}{L} }[/math]

Step 11

[math]\displaystyle{ ∆V = E * d }[/math]

Step 12 Substitute [math]\displaystyle{ E_{Hall} }[/math]

[math]\displaystyle{ ∆V = \frac{Emf * u * |B|* h}{L} }[/math]

Step 13 Plug in given values and solve for[math]\displaystyle{ ∆V }[/math]

[math]\displaystyle{ ∆V = -1.767*10^{-5} }[/math]

Explanation: The voltmeter reads the voltage of the bar between the given distance. Since this voltmeter is attached along the height of the bar, the distance is going to be the 3cm. We write out the Lorentz Force formula and set it equal to zero, which makes the magnetic force and electric force equal to each other. After manipulating the equation, the Hall Electric Field is drift sped times the magnetic field. The drift speed is found by manipulating the Current formula, Area density formula, and the Resistance Formula. After I is found, you plug it into the I in the drift speed formula, and plug drift speed v into the Hall electric field formula. Since Hall voltage is Hall electric times the distance, you multiply the calculated Hall electric field with 3 cm in order to get the final Hall voltage.

Click for Solution to #2

[math]\displaystyle{ I = \frac{Emf*q*n*u*A}{L} }[/math]

[math]\displaystyle{ I = 2.19927 A }[/math]

Explanation: You use the derivation of I from first portion of the question and plug in the values to calculate the conventional current. The Area here is the width times the height because the Ammeter is connected through the face created by the area of width and height.

Difficult

[math]\displaystyle{ B = 1.5 }[/math] T out of the page (denoted by concentric circles)

1. Calculate the drift speed v of the mobile charges
2. Calculate the charge density n of the mobile charges
3. ∆V = 13 V along the length of the bar, calculate the mobility u of the mobile charge carrier in the metal

Click for Solution to #1

Step 1 Find [math]\displaystyle{ E_{Hall} }[/math]

[math]\displaystyle{ ΣF_y = q(v\; Χ \;B) + q*E_{Hall} }[/math]

[math]\displaystyle{ 0 = q(v\; Χ \;B) + q*E_{Hall} }[/math]

[math]\displaystyle{ q(v\; Χ \;B) = q*E_{Hall} }[/math]

[math]\displaystyle{ E_{Hall} = (v\; Χ \;B) }[/math]

[math]\displaystyle{ E_{Hall} = v * B }[/math]

Step 2

[math]\displaystyle{ E_{Hall} = \frac{∆V_H}{h} }[/math]

Step 3 Substitute [math]\displaystyle{ E_{Hall} }[/math]

[math]\displaystyle{ v * B = \frac{∆V_H}{h} }[/math]

Step 4 Solve for v

[math]\displaystyle{ v = \frac{∆V_H}{h*B} }[/math]

Step 5 Plug in given values

[math]\displaystyle{ v = 1.367 }[/math] m/s

Explanation: First, set the Lorentz Force Equation equal to zero. After a couple of algebraic manipulations similar to the middling question, the Hall electric field equals to the product of the drift speed and magnetic field. Since, the hall electric field is not given but hall voltage is, you have to substitute the hall electric field with hall voltage divided by the height of the bar (distance that voltmeter calculated). Afterwards, plug in all the given values, and calculate for the drift speed.

Click for Solution to #2

Step 1

[math]\displaystyle{ I = |q|*n*A*v }[/math]

Step 2

[math]\displaystyle{ n = \frac{I}{|q|*A*v} }[/math]

Step 3 Plug in given values and solve

[math]\displaystyle{ n = 9.971 * 10^{23} /m^3 }[/math]

Explanation: In order to find the charge density of the mobile charge carriers use the conventional current formula. Manipulate the conventional current formula to find a formula for charge density and plug in all the values.

Click for Solution to #3

Step 1

[math]\displaystyle{ v = u*E }[/math]

Step 2 Find a formula for u

[math]\displaystyle{ u = \frac{v}{E} }[/math]

Step 3 Substitute for E using [math]\displaystyle{ ∆V = E*L }[/math]

[math]\displaystyle{ u = \frac{v*L}{∆V} }[/math]

Step 4 Plug in known and calculated values

[math]\displaystyle{ u = 2.41*10^{-3} }[/math]

Explanation: The drift speed of the charge carriers is the product of the electric field and mobility of the charge carriers. Since electric field is not given, but the voltage along the length of the bar is, you have to substitute the electric field with the given voltage divided by the length of the bar. Afterwards, plug in all the values given in the problem and the value calculated for the drift speed.

Applications

Hall effect is all about seeing the relationship between magnetic and electric forces while also remembering how metals polarize. This means that it has a lot of mechanical and machine applications. It can sense when a magnetic field or electric field changes, so it can control many machines, apply pressures, and report many values. All of these skills are very important for Mechanical Engineering, so this topic has a lot of relevance to my major. Moreover, a lot of engineering, in general, is about analyzing concepts before calculating values. The idea of the Hall Effect gives a lot of important data without the use of any numbers (of course it gives more info on the calculation of numbers). This reasoning process required for the Hall Effect is a very helpful skill for engineers to have.

Hall Effect Sensor with a magnet

Another field that takes advantage of the Hall Effect is Electrical Engineering thanks to the Hall Effect Sensor. Electrical engineers can use the hall effect sensor to record movement. As seen in the picture to the left, the sensor will increase its voltage the closer the magnet is to the sensor. In fact, a VIP group here at Georgia Tech, the VIP Hands-on Learning team, researched the possibility of using the sensor to measure the movement of a two-degree of freedom spring-mass system. Links to the VIP Research: https://vip.gatech.edu/wiki/index.php/Vibrations https://vip.gatech.edu/wiki/index.php/Hall_Effect_Sensor

Industrial

Hall Effects are used in industry to aid in the control of Hydraulic systems such as moving cranes and backhoes. It is also used to help sense a car wheel's motion to aid in the use of anti-skid/anti-lock brakes. Every smartphone today uses a hall effect sensor as well. This is how the digital compass of a cell phone works. The hall effect senses the change in magnetic field to approximate direction. Another great way of using the hall effect in smartphones is to lock the screen when a case cover is flipped. The cover has a magnet that the smartphone senses, so it locks the screen automatically when the cover is on the screen. A test for this feature can be seen in the following video: https://www.youtube.com/watch?v=ITbT5vrvhX8 .

Laboratory

Hall effect is also taken into consideration when hall probes are used as magnetometers.

A Hall probe is used to measure the difference of magnetic flux perpendicular to its sensor. This information is then fed to magnetometers to help read the difference in magnetic fields.

Hall effect sensor: http://www.ebay.com/sch/i.html?_nkw=hall+effect+sensor

Magnetometer: http://www.ebay.com/itm/EM2-EARTH-MAGNETOMETER-MAP-MAGNETIC-FIELDS-SURVEY-TOOL-/251324557405?hash=item3a841c685d:m:m8gnViuidubx7vMbMejiNNA

To use this idea in a lab, simply create a circuit through a conductive material, like a piece of foil, and calculate the direction of the magnetic field using right-hand rule. Use this information to then properly add the hall probes to the foil so they are perpendicular to the magnetic field, and then BOOM! You will have information to read to a magnetometer.

History

Edwin Herbert Hall

The Hall Effect was discovered in 1879 by Edwin Hall while attending Johns Hopkins University for his Doctoral Degree. While a solid mathematical groundwork for electric and magnetic phenomenon had already been discovered by James Clark Maxwell, many of the physical implications and practical uses for these theories was still being explored. The interaction of magnetic and electric fields was a particularly hot topic. Hall exposed a gold leaf (metal slab) to a magnetic field perpendicular to its surface and had current flow through the slab. He observed a potential difference perpendicular to the current and also the magnetic field. This means that potential is observed not only in the direction of current flow as usual. This is what led to Hall's discovery of the Hall Effect, originally published in his paper "On a New Action of the Magnet on Electric Currents".

Conclusion: Tips to remember

1. When a current carrying metal/conductor is placed in a magnetic field, a voltage is formed perpendicular to both current and magnetic field

2. The Hall effect is made when the charges create almost a polarized metal, as a result of being subject to a magnetic field perpendicular to the flow of electrons.

3. Right-hand rule whenever in doubt.

Hall effect can only be tested so many ways. There are a few tricks to keep in mind.

In the diagram above a voltmeter connected to a sheet of metal. Since the voltmeter reads a negative voltage, you can automatically assume that the side connected to the negative terminal of the voltmeter is connected to the positive side of the metal due to hall effect, because voltmeter is reading a charge in the opposite direction.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Combining Electric and Magnetic Forces

Biot-Savart Law for Currents

Lorentz Force

Further reading

Books, Articles or other print media on this topic

Matter and Interactions: Volume 2 by Ruth Chabay and Bruce Sherwood (4th Edition)

http://www.phys.utk.edu/labs/modphys/Hall%20Effect.pdf

External links

Internet resources on this topic

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/hall.html

https://www.youtube.com/watch?v=_ATDraCQtpQ

References

https://en.wikipedia.org/wiki/Hall_effect

http://www.nobelprize.org/nobel_prizes/physics/laureates/1998/press.html

https://en.wikipedia.org/wiki/Edwin_Hall

Matter and Interactions: Volume 2 by Ruth Chabay and Bruce Sherwood (4th Edition)

http://www.nasonline.org/publications/biographical-memoirs/memoir-pdfs/hall-edwin.pdf

http://www.electronics-tutorials.ws/electromagnetism/hall-effect.html

https://www.quora.com/What-is-the-use-of-Hall-effect-sensors-in-smartphones