Right Hand Rule
This topic covers Right Hand Rule. Claimed by: Bhavin Shah Spring 2025
The Main Idea
The right-hand rule is not just a mnemonic that teachers tell you to use—it’s a geometric consequence of how three-dimensional space is defined. Many physical quantities—such as angular momentum, torque, magnetic forces, and rotational motion—are fundamentally tied to the cross product, and the right-hand rule is what gives those quantities a consistent and meaningful direction. Understanding the intuition behind the RHR, combined with practice, allows us as students to move through problems more quickly on tests. By understanding the direction of the resultant vector, we can often use it to guide our work and even use it as a proxy to check whether our answers make sense.
Why We Need the Right-Hand Rule
When two vectors lie in a plane—say, the position vector r of a particle and its momentum vector p—their combination often represents something that is not confined to that plane. For example:
The angular momentum of a particle does not lie in the plane of motion. The magnetic force on a charge depends on a cross product and points perpendicular to the plane of the velocity and magnetic field. The torque exerted on an object is also perpendicular to the plane of applied force and lever arm. The cross product gives a vector that sticks straight out of the plane formed by the two original vectors. But there are two possible directions it could point—one on each side of the plane. The right-hand rule is the convention we use to pick the correct, consistent direction every time. Without this rule, the direction of quantities like torque, angular momentum, or magnetic force would be ambiguous.
A Mathematical and Computational Model
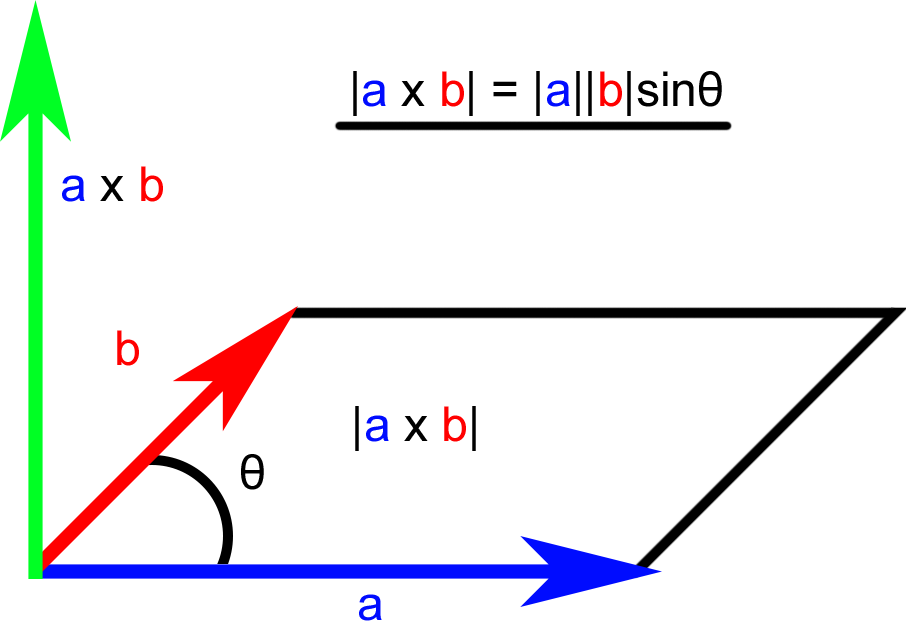
The direction of any quantity defined by a cross product—such as torque, magnetic force, or angular momentum—can be found by computing the cross product of two vectors. For any vectors 𝑎 a and 𝑏 b, the cross product
To calculate the cross product from a matrix, multiply each component by its corresponding determinant. Use this visual representation to help you.
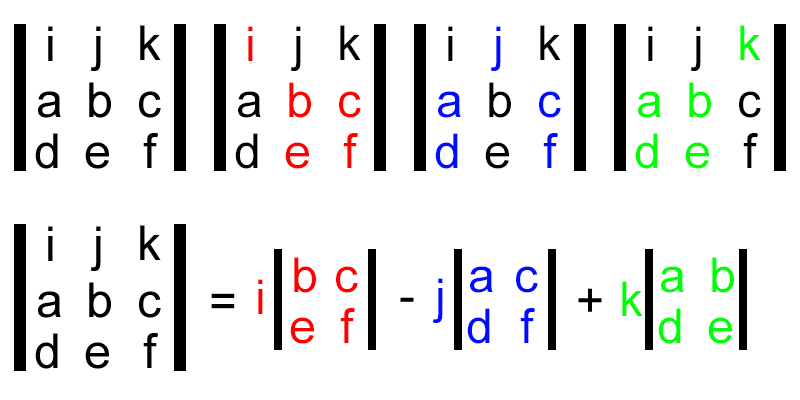
For more on the explanation of how to calculate cross product, visit this website: https://www.mathsisfun.com/algebra/vectors-cross-product.html
Here is an example problem. Solve first using the right hand rule, and then solve mathematically with the cross product.
For a computational model i have attached the trinket code below which provides a model of the the right hand rule cross-product.
https://trinket.io/glowscript/31d0f9ad9e
Answer:
The cross product should be <-12, 0, 0>
So the vector is in the -x direction, which the right hand rule also tells us.
Visualization
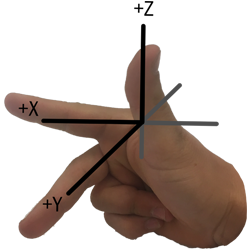
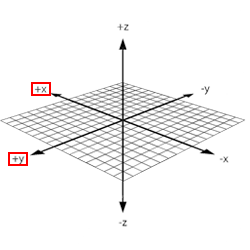
You can use your right hand to visualize the intuition of the Right Hand Rule. Consider the x-y-z space drawn with these axes from the origin:
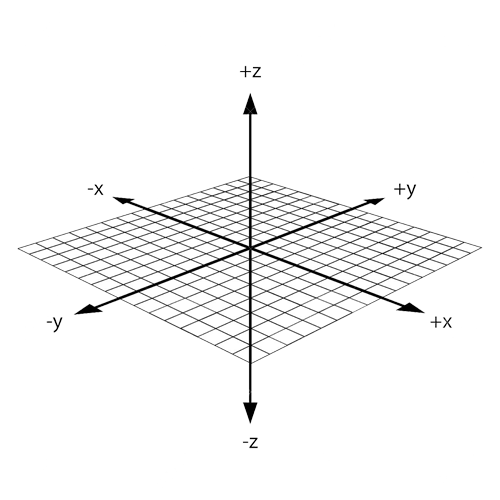
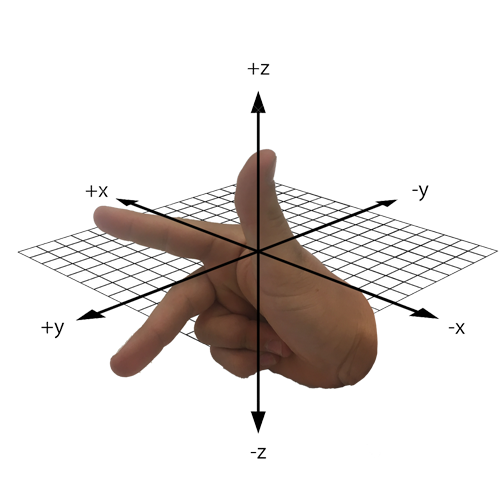
Now, take your right hand and point your index finger forward (the direction your arm faces), point your thumb up, and point your middle finger perpendicular to your index finger. Your thumb is the z-axis and points in the positive z-direction. Your index and middle fingers represent the x-y plane.
Your hand should look something like this:
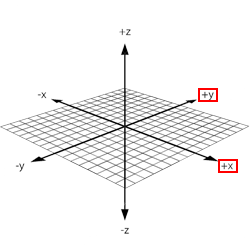
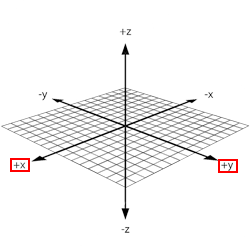
Then you can visualize the x-y-z axes over your hand like this:
Realize that you can rotate the x-y plane along the z-axis. For example, if you were to rotate the original x-y plane in 90 degree increments clockwise, you would see this:
Now, as you can see, your right hand indeed represents the entire x-y-z space.
Performing the Right Hand Rule
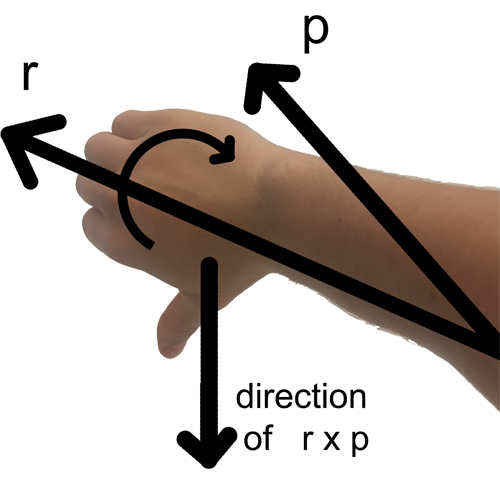
Right-Hand Rule: Extend your right arm so that it points in the direction of the r vector. Rotate your wrist so that your palm can curl toward the direction of the p (momentum) vector. Curl your fingers in the direction of p, and extend your thumb. The thumb now points in the direction of the unit vector that represents the angular momentum.
Hint: If the rotation is counterclockwise, your right thumb—and therefore the angular momentum vector—points out of the plane (+z direction). If the rotation is clockwise, the vector points into the plane (–z direction).
Right-Hand Rule (for magnetic fields around a current-carrying wire): Point your thumb in the direction of the current. Your curled fingers naturally wrap around the wire in the direction of the magnetic field lines.
Counterclockwise example:
When the direction from r to p is counterclockwise, your curled fingers match that motion, and your thumb points upward in the +z direction. This confirms that the angular momentum vector points out of the page.
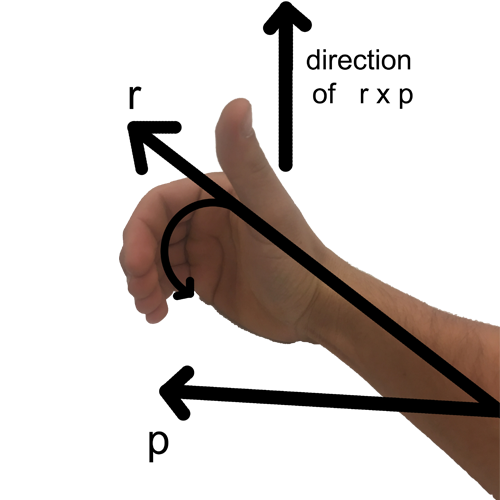
If the p vector is in the other direction relative to r, you would need to turn your hand upside down to curl your fingers towards it. In this case, your thumb points down in the -z direction!
This situation would also make your thumb point in the -z direction (Notice it is just the first image rotated 180 degrees).
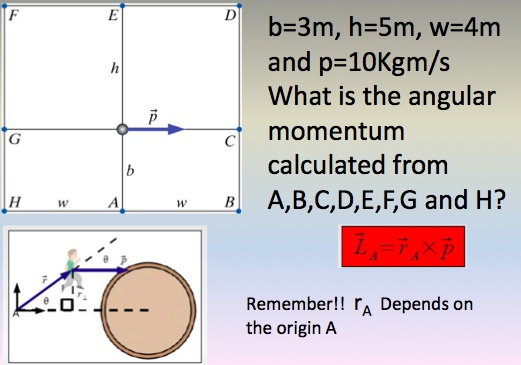
Examples
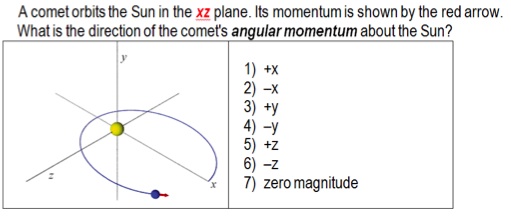
Ans: 4
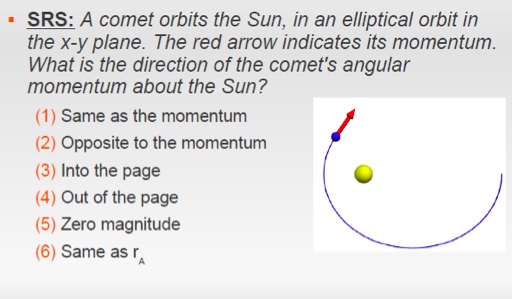
Ans: 3
Ans: 3
Ans: L(A)=L(B)=L(H) = <0, 0, -30> L(G)=L(C) = <0, 0, 0> L(D)=L(E)=L(F) = <0, 0, +50>
Connectedness
The Right Hand Rule is a very essential component of solving cross products, such as in Hall Effect, Angular Momentum, Lorentz force and more. The concept is usually very tricky to understand, so I wanted to give my best insight on what helped me understand exactly how and why it works. It also provides a proxy for right answers whcih will be useful in a testing environment.
History
The right-hand rule emerged in the 1800s as scientists sought a consistent method for describing directions in electricity, magnetism, and rotational motion. After Ørsted and Ampère showed that electric currents generate magnetic fields, physicists needed a standardized way to define the direction of those fields. James Clerk Maxwell later unified electricity and magnetism and adopted a right-handed coordinate system in his equations, helping solidify the convention. By the late 19th century, Josiah Willard Gibbs and Oliver Heaviside formally defined the modern vector cross product and specified its direction using the right hand, embedding the rule into vector calculus. Today, the right-hand rule is universally used to assign consistent directions to physical quantities such as torque, angular momentum, and magnetic forces.
See also
The Right Hand Rule is a crucial part in solving Angular Momentum and Torque problems.
External links
https://trinket.io/glowscript/31d0f9ad9e
https://www.mathsisfun.com/algebra/vectors-cross-product.html
https://teachingandlearninglabs.com/AllHTML/RightHandRule.shtml
References
The following pictures were created in Adobe Photoshop using pictures taken by me:
- Cross product visualization
- All Right Hand Rule visualization pictures
All pictures were taken from lecture slides to refrain from infrangement.
https://www.vecteezy.com/vector-art/25747595-fleming-s-right-hand-rule