Potential Difference at One Location
Written by Alex George
The Main Idea
Potential difference is usually defined as the change in the potential between two distinct points. However, it is also useful to determine potential at a single location of interest.
In this case, we must define the potential at a location (ex. Location A) as the potential difference between a point infinitely far from all other charged particles and the location we defined.
As potential has a value at all locations at space, it is a scalar field, not a vector field.
A Mathematical Model
The Potential at One Location
[math]\displaystyle{ V_{a} = V_{a} - V_{\infty } }[/math] where [math]\displaystyle{ V_{a} }[/math] is the potential location of interest and [math]\displaystyle{ V_{\infty } }[/math] is the potential at a location infinitely far away.
This equation is only valid when [math]\displaystyle{ V_{\infty } }[/math] is equal to zero.
Potential near a Point Charge
Parameters: A point charge with charge [math]\displaystyle{ q }[/math]. We are a distance [math]\displaystyle{ x }[/math] from this point charge and we want to find the potential difference between our point charge and the potential at infinity.
[math]\displaystyle{ V_{x} = V_{x} - V_{\infty } = -\int_{\infty }^{x} \frac{1}{4\pi\varepsilon _{0} } \frac{q}{x^2} dx = \frac{1}{4\pi\varepsilon _{0} } (\frac{q}{x}-\frac{q}{\infty}) = \frac{1}{4\pi\varepsilon _{0}} \frac{q}{x} }[/math]
The sign of the potential depends on the sign of the charge on the particle:
if [math]\displaystyle{ q \lt 0, V_{x} \lt 0 }[/math]
if [math]\displaystyle{ q \gt 0, V_{x} \gt 0 }[/math]
Potential Energy at a Single Location
Once the value of the potential at one location is known, the potential energy of a system can be calculated.
If a charged object was placed at the location where the potential is known, then the potential energy of the system would be given the the equation:
[math]\displaystyle{ U_{A} = qV_{A} }[/math]
Substituting in the derived equation from the previous section for [math]\displaystyle{ V_{A} }[/math], we obtain the following:
[math]\displaystyle{ U = q_{1} (\frac{1}{4\pi\varepsilon _{0}} \frac{q_{2}}{x}) = (\frac{1}{4\pi\varepsilon _{0}} \frac{q_{1}q_{2}}{x}) }[/math] where [math]\displaystyle{ x }[/math] is the separation between the two particles, and [math]\displaystyle{ q_{1} }[/math] and [math]\displaystyle{ q_{2} }[/math] are the respective charges of the particles.
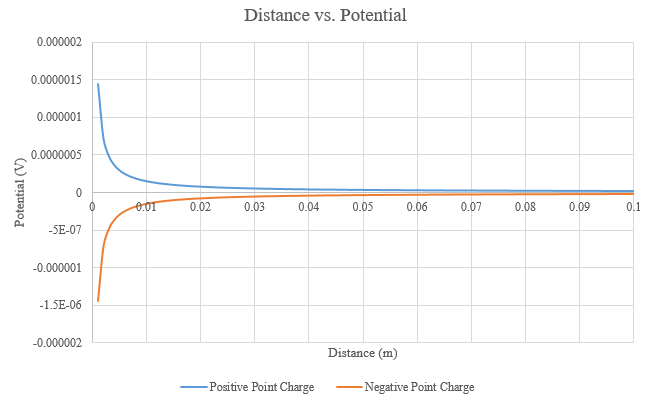
A Visual Model
A visualization of Distance vs. Potential from a point charge is given by Figure 1:
Figure 1. Potential vs. Distance for a Point charge with Charge [math]\displaystyle{ e }[/math]
The electric field of the point charge can be obtained by differentiation. The negative gradient of the potential with respect to distance would yield the electric field:
[math]\displaystyle{ E_{x} = -\frac{\partial V}{\partial x} }[/math]
Here is a video explaining the above concepts with more examples [1].
Examples
Here are a couple of problems that illustrate the concepts presented above.
Simple Examples
Example 1 - Potential at a Location Near a Sphere
What is the electric potential 5 cm away from a 1 cm diameter metal sphere that has a -3.00 nC static charge?
Solution:
As the distance from the center of the sphere is greater than the radius, we can treat the metal sphere as a point charge.
From the above derivation of the potential for a single point charge, we have:
[math]\displaystyle{ V_{x} = V_{x} - V_{\infty } = -\int_{\infty }^{x} \frac{1}{4\pi\varepsilon _{0} } \frac{q}{x^2} dx = \frac{1}{4\pi\varepsilon _{0} } \bigg(\frac{q}{x}-\frac{q}{\infty} \bigg) }[/math]
[math]\displaystyle{ V_{x} = 9\times 10^{9} \frac{N\cdot m^{2}}{C^{2} } \bigg(\frac{-3.00\times 10^{-9}\ C}{5.00\times 10^{-2}\ m}-\frac{-3.00\times 10^{-9}\ C}{\infty}\bigg) = 9\times 10^{9} \frac{N\cdot m^{2}}{C^{2} } \frac{-3.00\times 10^{-9}\ C}{5.00\times 10^{-2}\ m} = -539 V }[/math]
Example 2 - Charge Required to Produce a Specific Potential
What is the excess charge on a Van de Graff generator that has a 25.0 cm diameter metal sphere that produces a voltage of 50 kV near the surface?
Solution
The potential of the surface will be the same as that of a point charge from the center of the sphere, 12.5 cm away. The excess charge can be derived from the equation for potential a distance away from a point charge:
[math]\displaystyle{ V_{x} = \frac{1}{4\pi\varepsilon _{0} } \bigg(\frac{q}{x}\bigg) }[/math]
[math]\displaystyle{ q = {4\pi\varepsilon _{0}} x V_{x} }[/math]
[math]\displaystyle{ q = \frac{1}{9\times 10^{9}} \frac {N\cdot m^{2}}{C^{2}} (12.5 \times 10^{-2} \ m) (50 \times 10^{3} \ V) = 6.94 \times 10^{-7} \ C }[/math]
Difficult Examples
Example 1 - Potential Along the Axis of a Ring
What is the potential a distance [math]\displaystyle{ z }[/math] from the center of the ring?
Solution:
The electric field of a ring is given by the following equation:
[math]\displaystyle{ E_{z,ring} = \frac{1}{4\pi\varepsilon _{0} } \frac {Qz}{(R^{2}+z^{2})^{\frac {3}{2}}} }[/math] where [math]\displaystyle{ z }[/math] is the distance from the center of the ring, [math]\displaystyle{ R }[/math] is radius of the ring, and [math]\displaystyle{ Q }[/math] is the charge on the ring.
This equation can be integrated with respect to [math]\displaystyle{ z }[/math] and the appropriate bounds to obtain the potential at a location [math]\displaystyle{ z }[/math] from the center of the ring:
[math]\displaystyle{ V_{z,ring} = -\int_{\infty}^{z} \frac{1}{4\pi\varepsilon _{0} } \frac {Qz}{(R^{2}+z^{2})^{\frac {3}{2}}} dz }[/math]
[math]\displaystyle{ V_{z,ring} = \frac{1}{4\pi\varepsilon _{0} } \frac {Q}{\sqrt{R^{2}+z^{2}}} }[/math]
Connectedness
- How is this topic connected to something that you are interested in? This topic is related to the concept of Potential Energy, or the capacity to do work in a system. Electric Potential is a derivation of potential energy and is a convenient way to express potential in terms of electric potential energy per unit charge. I am interested in bio instrumentation, so this concept has direct relevance in terms of circuit analysis and design.
- How is it connected to your major? My major is biochemistry and electric potential has several applications in biological systems. For instance, in mechanisms such as the firing of a neuron's action potential, the electric potential across the neuronal membrane must reach certain thresholds in order to propagate the neural signal.
- Is there an interesting industrial application? Electric potential has various applications in industry, particularly in the aspects of circuit design and analysis. A particular implementation in medicine would be a defibrillator.
History
The SI unit for electric potential is the volt, which is named in honor of the Italian physicist Count Alessandro Volta (1745-1827), who invented the voltaic pile, the first chemical battery.
Volta had developed the voltaic pile using an effective pair of metals (zinc and silver) to create a steady electric current in the 1880s.
Today, the "conventional" volt is used and was defined in 1988 by the 18th general conference on Weights and Measures and adopted in 1990. The Josephson effect was employed to produce an exact frequency to voltage conversion and a cesium frequency standard is used to define the modern volt.
More information on Alessandro Volta can be found at Wikipedia [2] .
See also
Potential Difference in a Uniform Field
Potential Difference Path Independence
Potential Difference of point charge in a non-Uniform Field
Potential Difference in an Insulator
Further reading
Chabay, Ruth W. Matter and Interactions, Ch. 16.7. 4th ed. New York: Wiley, 2015. Print.
Urone, Paul Peter., et al. College Physics, Ch. 19.3. Houston, Texas: OpenStax College, Rice University, 2013. Print.
External links
Youtube Video on Electric Potential of a Point Charge
References
Chabay, Ruth W. Matter and Interactions. 4th ed. New York: Wiley, 2015. Print.
Urone, Paul Peter., et al. College Physics. Houston, Texas: OpenStax College, Rice University, 2013. Print.
Wikipedia.org