Kirchoff's Laws
Edits: Emma Hardin, Spring 2024
Kirchoff's Laws are two fundamental principles of electric circuits and are used to determine the behaviors of electric circuits and their components. They serve as a guide for how circuits will behave and are accurate for all DC and low-frequency AC circuits. These principles are used to measure voltage and current in voltmeters and ammeters.
Kirchoff's First Law, also known as Kirchoff's Node Rule or Kirchoff's Junction Rule, further exercises the law of Conservation of Charge and states that if current is constant, all the current that flows through one junction must be equal to all the current that flows out of the junction. This rule can be applied both to conventional and electron currents. This rule is not a fundamental principle, but rather a consequence of the fundamental principle of conservation of charge and the definition of steady-state. This law essentially states that the net amount of current entering a particular juncture in the system is equal to the net amount of current leaving the system. A mathematical way to think about is that the sum of the currents entering a point will be equal to the sum leaving it.
Kirchoff's Second Law, also known as Kirchhoff's Loop Rule or Kirchhoff's Voltage Law states that the sum of potential differences around a closed circuit is equal to zero. More simply, in a completed circuit, the voltages around a loop will sum to 0. This is because voltage is just energy per unit charge, and both energy and charge are conserved by fundamental laws. A good way to think about this is by attaching a positive value to the points in the loop that contribute to the net voltage, and by attaching a negative value to the resistors. The amount of voltage that enters the loop will be equal to the amount that is dissipated across the loop, thus ensuring that the net voltage is zero.
Note that this is only true when the magnetic field is neither fluctuating nor time-varying. If a changing magnetic field links the closed loop, then the principle of energy conservation does not apply to the electric field, causing the Loop Rule to be inaccurate in this scenario.
Both laws have limitations; most specifically, the node rule relies on the net charge in the system being constant, while loop rule depends on time-varying magnetic fields being confined to singular parts.
The Main Idea
Kirchoff's Node Rule
The node rule states that at any junction in an electrical circuit, the amount of current flowing into the junction is equal to the amount of current flowing out of the junction in steady-state.
In the steady state, for many electrons flowing into and out of a node,
- electron current: [math]\displaystyle{ net\ i_{in} = net\ i_{out}, }[/math] where [math]\displaystyle{ i = nA\mu }[/math][math]\displaystyle{ E }[/math]
- conventional current: [math]\displaystyle{ net\ I_{in} = net\ I_{out}, }[/math] where [math]\displaystyle{ I = |q|nA\mu }[/math][math]\displaystyle{ E }[/math]
Conservation of Charge
This rule is an application of the conservation of electric charge, basically that charge within a circuit cannot be created or lost. During the flow process around the circuit, there is no loss of any charge, thus the total current in any cross-section of the circuit is the same. If there are no nodes in the loop, the conventional current is the same throughout the loop. This also why the node rule relies on a constant charge throughout the system; if the charge was constantly changing, then the node rule will not apply. The node rule essentially states that the net current entering a juncture in the system will always be constant.
Kirchoff's Loop Rule
The loop rule simply states that in any round trip path in a circuit, Electric Potential equals zero. This applies through any round trip path; in more complex circuits, there can be multiple round trip paths. This principle is an application of the conservation of energy, specifically within a circuit. This principle is often used to solve for resistance or current passing through of light bulbs and other resistors, as well as the capacitance or charge of capacitors in a circuit.
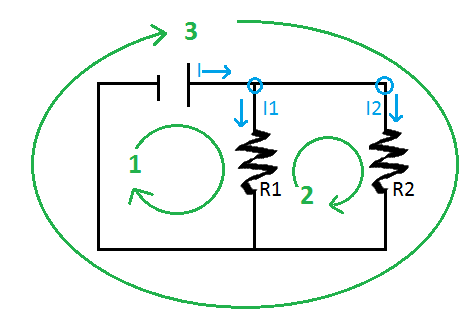
LOOP 1: [math]\displaystyle{ \Delta {V}_1 = emf - I_1R_1 = 0 }[/math]
LOOP 2: [math]\displaystyle{ \Delta {V}_2 = I_1R_1 - I_2R_2 = 0 }[/math]
LOOP 3: [math]\displaystyle{ \Delta {V}_3 = emf - I_2R_2 = 0 }[/math]
To figure out the sign of the voltages, act as an observer walking along the path. Start at the negative end of the emf and continue walking along the path. The emf will be positive in the loop rule because you are moving from low to high voltage. Once you reach a resistor or capacitor, this will be negative in the loop rule equation because it is high to low voltage. Continue along the path until you return to the starting position.
Bringing Both Laws Together
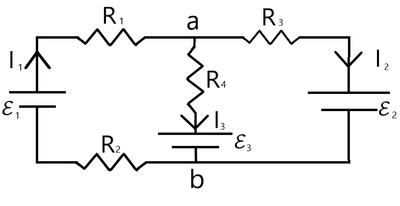
Find all possible node and loop equations for the following circuit.
You should have 3 Loop Equations and 2 Node equations.
Some examples:
[math]\displaystyle{ I_1= I_2+I_3 }[/math]
[math]\displaystyle{ I_1*R_1 + emf_1 + emf_3 + I_3*R_4 = 0 }[/math]
Matrices in Conjunction with Kirchhoff's Laws
After creating loop equations for all possible loops in a circuit using the node rule and loop rule, you can input the coefficients of the equations into a matrix. After inputting it into the matrix, you can use linear algebra and row reduction in order to solve for the current or resistances of the different parts of the circuit. This format and method of understanding complex circuits are especially useful for circuits with a large number of loops as it makes the algebra involved in getting the currents much simpler and straightforward. Simply creating the equations for every loop possible and every node and then inputting the coefficients into a row reduction calculator can give you all the values for I and/or R that you might need.
After finding the loop equations you can use a matrix calculator as well to further simplify your task!: Online Matrix Row Reduction Calculator
You can alternatively use a system of equations to find currents, resistance, or capacitors (for when you don't know linear algebra or do not have a calculator present
An example of how you would format the matrix of a Kirchhoff's law problem is shown below:
- [math]\displaystyle{ \mathbf{A} = \begin{bmatrix} R1 & R2 & R3 & | EMF \\ & & & | EMF \\ & & & | EMF \end{bmatrix}. }[/math]
Simply place to coefficients or resistances of each of the different resistors as separate elements in the columns of the matrix while keeping track of which resistance pertains to which part of the loop and place the EMF of that loop as the solution column in the augmented matrix. Then after row reducing, each of the resistors should be simplified so that there is a 1 in at least 1 row for every resistor and the current at the end of that row is the current for the resistor that is in the same column as the 1 in the row of the current.
For example in the matrix below the current going through R2 is 1/15 amps:
- [math]\displaystyle{ \mathbf{A} = \begin{bmatrix} R1 & R2 & R3 & | EMF \\ & 1 & & | 1/15 \\ & & & | EMF \end{bmatrix}. }[/math]
Limitations
The Node rule assumes that current flows only in conductors and that whenever current flows into one end of a conductor it immediately flows out the other end. This is not a safe assumption for high-frequency AC circuits. In other words, the node is valid only if the total electric charge, [math]\displaystyle{ Q }[/math], remains constant in the region being considered. In practical cases, this is always so when the node rule is applied at a point.
The Loop rule is based on the assumption that there is no fluctuating magnetic field linking the closed-loop. This is not a safe assumption for high-frequency AC circuits. In the presence of a changing magnetic field, the electric field is not a conservative vector field. Therefore, the electric field cannot be the gradient of any potential. That is to say, the line integral of the electric field around the loop is not zero, directly contradicting KVL.
Understanding these limitations is essential to understanding how motional emf, motors, and generators work.
A Mathematical Model
Kirchoff's Node Rule

The node rule can be stated as:
- [math]\displaystyle{ \sum \Delta{I} = 0 }[/math]
where [math]\displaystyle{ I }[/math] stands for the current of the individual parts or wires in a circuit and the sign of the current that flows into the junction is opposite of the current that flows out of the junction. This simply supports the idea that charge cannot be created or destroyed because the total current must remain equal regardless of the path it takes.
- [math]\displaystyle{ \sum_{k=1}^n I_k = 0 }[/math]
where [math]\displaystyle{ n }[/math] is the total number of branches with current flowing through the node, as well as along any node in a circuit:
- [math]\displaystyle{ \Delta {I}_{1} + \Delta {I}_{2} + \space.... = 0 }[/math]
or more generally:
- [math]\displaystyle{ \sum_{k=1}^n \tilde{I_k} }[/math] = 0
Another definition is simply a summation rule: "[math]\displaystyle{ \sum I(in) = \sum I(out) }[/math] Kirchoff's Loop Rule
A mathematical representation is:
- [math]\displaystyle{ \sum \Delta{V} = 0 }[/math]
where [math]\displaystyle{ V }[/math] stands for the voltage of the individual parts or wires in a circuit and the sign of the voltage that flows clock-wise is opposite of the current that flows counterclockwise. This simply supports the idea that energy cannot be created or destroyed because the total current must remain equal regardless of the path it takes.
- [math]\displaystyle{ \sum_{i=1}^n {V}_{i} = 0 }[/math]
where [math]\displaystyle{ n }[/math] is the number of voltages being measured in the loop, as well as
- [math]\displaystyle{ \Delta {V}_{1} + \Delta {V}_{2} + \space.... = 0 }[/math]
along any closed path in a circuit. The voltages may also be complex:
- [math]\displaystyle{ \sum_{k=1}^n \tilde{V}_k = 0 }[/math]
Matrix Intrepretation
Using matrices can simplify the process of using node and loop rules in order to find out different parts of a complex circuit. Simply write out all the loop and node rules for a circuit. Then place coefficients of the equations you created in a matrix in the format below. The matrix should be an augmented matrix with the elements on the left being the resistances and the right being the EMF of that loop.
- [math]\displaystyle{ \mathbf{A} = \begin{bmatrix} R1 & R2 & R3 & | EMF \\ & & & | EMF \\ & & & | EMF \end{bmatrix}. }[/math]
To row reduce you should add, subtract, multiply, interchange or add a multiple of rows to each other until the matrix is as far simplified as possible. This is mostly related to concepts from linear algebra. A good way to think about is algebraic manipulation: the goal is get simple terms in the matrix through normal mathematical manipulations.
A Computational Model
Click here for a computational model of an online circuit simulator. It opens up with an LRC circuit that has current running through it. The graphs on the bottom show the voltage as the current runs through the circuit. You can see that after a full loop the voltage is 0, verifying the loop rule. The voltage is always conserved, as long as the node rule can apply.
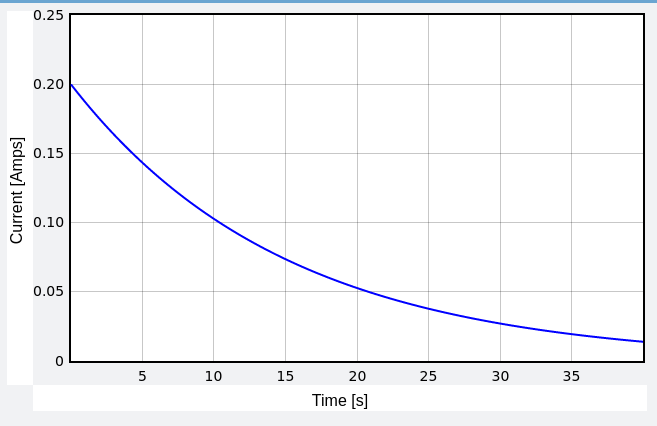
Another computational model, taken from an open source article is given here. This depicts the loop rule in a RC circuit with a bulb. It depicts how the net voltage in the bulb tends to zero over time, thus signifying a physical example of the loop rule in action. The Glowscript code can be found here. The result is shown below:
Examples
Simple
Question

Figure 1 displays a node in a circuit. I1 is equal to 10 amps. I2 is equal to 4 amps. What is I3?
Solution
- The current flowing into the node: [math]\displaystyle{ I_1 = 10A }[/math]
The current flowing out of the node: [math]\displaystyle{ I_2 + I_3 }[/math]
We know that the current flowing in must equal the current flowing out, so [math]\displaystyle{ 10A = 4A + I_3 }[/math]
Therefore [math]\displaystyle{ I_3 }[/math] must equal 6A.
Question
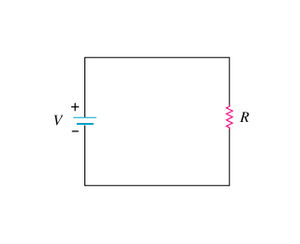
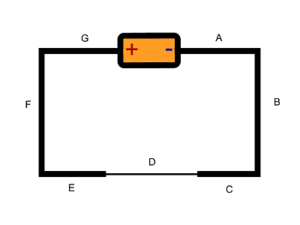
The circuit shown above consists of a single battery and a single resistor. The resistance of the wires is negligible for this problem.
If the [math]\displaystyle{ emf }[/math] is 5 V and the resistance of the resistor is 10 ohms, what is the current passing through the resistor?
Solution
Although we can solve this using the [math]\displaystyle{ V = IR }[/math] equation for the whole loop, let's examine this problem using the loop rule equation.
The loop rule equation would be [math]\displaystyle{ {V}_{battery} - {V}_{resistor} = 0 }[/math]
Since we know the [math]\displaystyle{ emf }[/math] of the battery we just need to find the potential difference through the resistor. For this we can use the equation of [math]\displaystyle{ V = IR }[/math].
Thus we now have an loop rule equation of [math]\displaystyle{ emf - IR = 0 }[/math] From here it is a relatively simple process to find the current. We can rewrite the loop rule equation as [math]\displaystyle{ emf = IR }[/math] and then plug in 5 for the emf and 10 for the resistance, leaving us with I = .5 amperes.
Middling
Question
The circuit shown above consists of a single battery, whose [math]\displaystyle{ emf }[/math] is 1.3 V, and three wires made of the same material, but having different cross-sectional areas. Let the length of the thin wires be [math]\displaystyle{ {L}_{thick} }[/math] and the length of the thin wire be [math]\displaystyle{ {L}_{thin} }[/math] Find a loop rule equation that starts at the negative end of the battery and goes counterclockwise through the circuit.
Solution
When beginning this problem, you must notice that the difference in cross-sectional areas affects the electric field in each wire. Because of this we will denote the electric field at D. as [math]\displaystyle{ {E}_{D} }[/math] and the electric field everywhere else as [math]\displaystyle{ {E}_{A} }[/math]. To begin we will go around the circuit clockwise and add up each component. First, we know that the [math]\displaystyle{ emf }[/math] of the battery is 1.3 V. Then, we will add up the potential voltage of each of the wires.
Remember that the electric potential of a wire is equal to the product of the electric field and the length of the wire. From this we can now find the potential difference of each section of the wires. The electric potential of location A-C is [math]\displaystyle{ {E}_{A} * {L}_{thick} }[/math]. This is the same for the electric potential of locations E - G of the wire. For the thin section of the wire, the electric potential is [math]\displaystyle{ {E}_{D} * {L}_{thin} }[/math]. From here we just go around the circuit counterclockwise and add each potential difference to the loop rule equation.
Thus we can find that a loop rule equation is: [math]\displaystyle{ emf - 2 ({E}_{A} * {L}_{thick}) - {E}_{D} * {L}_{thin} = 0 }[/math]
This can also be rewritten as: [math]\displaystyle{ emf = 2 ({E}_{A} * {L}_{thick}) + {E}_{D} * {L}_{thin} = 0 }[/math]
Difficult
Question
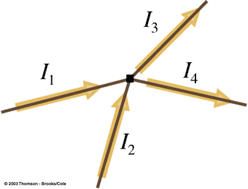
In Figure 2, I1 equal 23 amps, I2 equals 5 amps and I3 equals 42 amps. What is I4?
Solution
- The current flowing into the node: [math]\displaystyle{ I_1 + I_2 = 23A + 5A = 28A }[/math]
The current flowing out of the node: [math]\displaystyle{ I_3 + I_4 = 42A + I_4 }[/math]
Applying the node rule by using substitution, [math]\displaystyle{ I_4 = -14A }[/math]
But how could we get a negative current? This negative current implies that [math]\displaystyle{ I_4 }[/math] flows in the opposite direction of what we assumed. A negative current in a loop rule problem implies that a current is in the opposite direction.
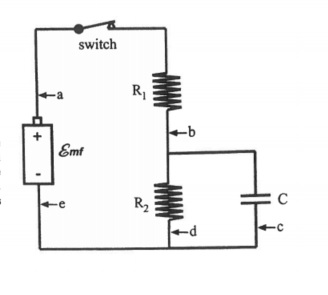
Question
For the circuit above, imagine a situation where the switch has been closed for a long time. Calculate the current at a,b,c,d,e and charge Q of the capacitor. Answer these using [math]\displaystyle{ emf, {R}_{1}, {R}_{2}, and \space C }[/math]
Solution
First, write loop rule equations for each of the possible loops in the circuit. It is advised, if given a paper version/one that can be edited, to draw the different nodes and loops on the image itself. This helps prevent careless errors. There are 3 loop equations that are possible.
[math]\displaystyle{ emf - {I}_{1}{R}_{1} - {I}_{2}{R}_{2} = 0 }[/math]
[math]\displaystyle{ emf - {I}_{1}{R}_{1} - Q/C = 0 }[/math]
[math]\displaystyle{ {I}_{2}{R}_{2} - Q/C = 0 }[/math]
From here, we can then solve for the current passing through a,b,d and e. We also know that the current passing through these points must be the same so [math]\displaystyle{ {I}_{1} = {I}_{2} }[/math]
[math]\displaystyle{ emf - {I}_{1}{R}_{1} - {I}_{1}{R}_{2} = 0 }[/math]
[math]\displaystyle{ emf = {I}_{1}({R}_{1} + {R}_{2}) = 0 }[/math]
[math]\displaystyle{ emf/({R}_{1} + {R}_{2}) = {I}_{1} }[/math]
So the current at [math]\displaystyle{ a,b,d,e = emf/({R}_{1} + {R}_{2}) }[/math]
You must also know that once a capacitor is charging for a long time, current no longer flows through the capacitor. We can then easily solve for c because since current is no longer flowing through the capacitor, the current at c = 0.
We will use the loop rule equation of [math]\displaystyle{ {I}_{2}{R}_{2} - Q/C = 0 }[/math] to solve for Q.
[math]\displaystyle{ {I}_{2}{R}_{2} = Q/C }[/math]
[math]\displaystyle{ C*({I}_{2}{R}_{2}) = Q }[/math] Since [math]\displaystyle{ {I}_{1} = {I}_{2} }[/math]
[math]\displaystyle{ C*({I}_{1}{R}_{2}) = Q }[/math]
We will plug in what we found {I}_{1} equals from before.
[math]\displaystyle{ C* (emf/({R}_{1} + {R}_{2})){R}_{2}) = Q }[/math]
Lastly, [math]\displaystyle{ Q = C* (emf/({R}_{1} + {R}_{2})){R}_{2} }[/math] and we have now solved the problem.
Current at [math]\displaystyle{ a,b,d,e = emf/({R}_{1} + {R}_{2}) }[/math]
Current at [math]\displaystyle{ c = 0 }[/math]
[math]\displaystyle{ Q = C* (emf/({R}_{1} + {R}_{2})){R}_{2} }[/math]
Question (USING MATRICES)
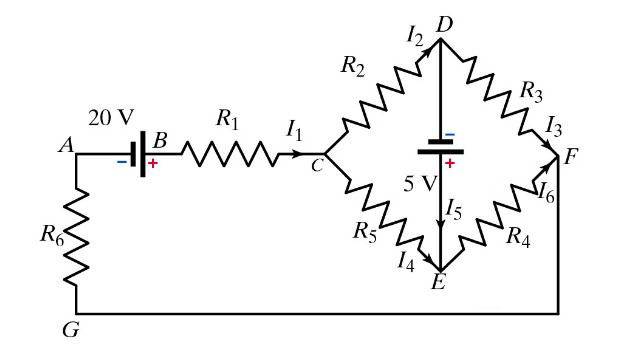
Six identical resistors and two different batteries are connected in a circuit as shown in the diagram. One of the batteries has a potential difference of 20 V and the other has a potential difference of 5 V. The direction of the currents in the circuit are indicated and labeled. Solve your loop and node equations to determine the current through resistorR6. The resistance of each resistor is 100 Ω.
Solution
From the diagram, it is evident that this particular problem will require quite a few loop and node rule equations, 11 total to be exact. To figure out the current through resistor R6 we will need to set up the node and loop rule equations in order to have a system of equations that will have enough variables and coefficients in order to be able to solve for this current.
The node equations are:
0 = I1 - I3 - I6
0 = I1 - I2 - I4
0 = I2 - I3 - I5
0 = I4 + I5 - I6
The loop rule equations are:
0 = -emf1 + (R1 + R4)I1 + (R5)I4 + (R4)I6
0 = -emf1 + (R1 + R6)I1 + (R2)I2 + (R3)I3
0 = -emf1 + (R1 + R6)I1 + (R2)I2 + emf2 + (R4)I6
0 = (R2)I2 + (R3)I3 - (R4)I6 - (R5)I4
0 = (R2)I2 - emf2 - (R5)I4
0 = (R3)I3 - (R4)I6 + emf2
0 = -emf1 + (R1 + R6)I1 + (R5)I4 + emf2 + (R3)I3
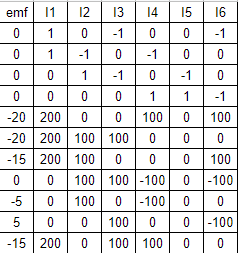
Now that we have the equations instead of taking the time to solve the system of equations for all 11 of these equations, we can simply use a matrix and row reduce in order to find the current is going through R6 as we should have enough relationships to deduce this. The matrix for this particular problem would be the following:
In the matrix above, the headers at the top represent what the coefficients in the matrix pertain too, being the emf and the resistances associated with each of the currents form I1 through I6. Now using a row reduction calculator we can make an augmented matrix with the results being the emf column and the currents and associated resistances being on the LHS and we can find the I in the right hand column of the augmented matrix that is associated with the correct part of the circuit we are looking for and that will be our result for the current through the circuit at that resistor. In this case, that ends up being 1/15 amps.
In this particular problem, using traditional system of equation methods would prove problematic and time consuming as there are 11 equations that we have to work with. Thus, by using a matrix and row reduction, we can simply place the coefficients into a matrix, row reduce, and look at the number that is in the column of the resistor we are trying to find the current for and that will be our solution.
Connectedness
The Node Rule is connected to a lot of other topics in physics. The loop rule is the most important one, as the node rule and loop rule in conjunction allow us to solve circuits. The node rule is also connected to other concepts such as voltage, current and electricity. The Node Rule also supports the law of conservation of energy because in essence, current is simply the flow of electric charge, and since you cannot (at least as of now) create energy or electrons out of nothing, everything that is put into the system must come out somehow. Therefore, all the current that is applied, must come out the other end. Kirchoff's laws preceeded Maxwell's, and played a key part in his equations.
The Loop Rule is simply an extension of the conservation of energy applied to circuits. Circuits are ubiquitous as they are featured in almost every technology today. Our understanding of these technologies is rooted in the empirical discoveries made in the mid 19th century, and further boosted by the the advancement of theoretical knowledge due to the likes of Faraday and Maxwell.
Perhaps the most interesting thing about Kirchoff's rules is that they can be derived from the fundamental laws of physics, and thus do not be explicitly memorized. They are simply extensions of the energy concepts we already know to be true.
One interesting note about Loop Rule is that is does not apply universally to all circuits. In particular, AC (alternating current) circuits at high frequencies, have a fluctuating electric charge that changes direction. This causes the electric potential of a round trip path around the circuit to no longer be zero. However, DC (direct current) circuits, and low frequency circuits in general, still follow the loop rule.
These laws allow for voltmeters and ammeters to work, with voltmeters having a high resistance and being connected in parallel and ammeters having a low resistance and being connected in series.
Linear algebra is also intertwined with Kirchhoff's laws involving loops and nodes as complex and large circuits with many components can often lead to many different loops and the amount of loop and node equations can often get out of hand very quickly. As a result, we can use matrices to simplify the algebra involved with solving for currents in components that are a part of large circuits with many different loop and node equations. After creating the matrix we need skills from linear algebra in order to find the row reduced form of the augmented matrix that we create. With this reduced version of the matrix, we can find the current or resistances of the different parts of the circuit in a much easier and more timely fashion.
Applications
Circuit Design
Kirchhoff's Laws are vital when designing electrical circuits as well as when we are analyzing them. The circuits that these laws can help us design and analyze can range from those found in our household appliances to more complex ones used in industrial applications at a large scale. In engineering, these laws are relevant because they help us design circuits that meet specific performance requirements.
Current Measurement
Kirchhoff's Laws can be used to measure the current flowing at various specific points of a circuit. By applying these laws at specific locations in a circuit, it can help us determine the amount of current entering and leaving that location or node. This aids us when we want to measure and control the flow of current in a circuit while designing or analyzing said circuit.
Voltage Measurement
Kirchhoff's Laws can be used to measure the voltage at different points of a circuit. By applying these laws to a loop in a circuit, it can help us determine the amount of voltage across all the points in that loop. This aids us when we want to measure and control the voltage levels in a circuit while designing or analyzing said circuit.
History

Gustav Kirchhoff (1824-1887) was a German physicist who is credited for the theory of spectrum analysis and Kirchoff's Laws (1845) among other accolades. There are many equations and laws named after him that he helped to discover. His circuit laws (the node rule and loop rule) were the first laws that he conceived, and discovered this during his time as a student at Albertus University of Königsberg in 1845; he later wrote his doctoral dissertation on these laws. Kirchoff went on to explore the topics of spectroscopy and black body radiation after his graduation from Albertus at the University of Berlin (when he became a lecturer, professor, and eventually chair of mathematical physics). In addition to his circuit laws, he is also known for his law of thermochemistry, determining the composition of the Sun, and the three laws of spectroscopy, the latter of which helped lead to quantum mechanics.
See Also
Further Reading
External Links
https://en.wikipedia.org/wiki/Kirchhoff%27s_circuit_laws#Kirchhoff.27s
http://www.tutorvista.com/content/physics/physics-iv/current-electricity/kirchhoffs-rules.php
http://physics.bu.edu/~duffy/py106/Kirchoff.html
https://www.mathportal.org/algebra/solving-system-of-linear-equations/row-reduction-method.php
References
- Matter & Interactions 4th Edition by Ruth W. Chabay & Bruce A. Sherwood
- http://www.math.odu.edu/~bogacki/cgi-bin/lat.cgi?c=roc
- http://www.regentsprep.org/Regents/physics/phys03/bkirchof1/
- https://www.mathportal.org/algebra/solving-system-of-linear-equations/row-reduction-method.php
- https://en.wikipedia.org/wiki/Kirchhoff%27s_circuit_laws#Kirchhoff.27s
- https://en.wikipedia.org/wiki/Kirchhoff%27s_circuit_laws#Kirchhoff.27s_voltage_law
- https://www.khanacademy.org/science/electrical-engineering/ee-circuit-analysis-topic/ee-dc-circuit-analysis
- http://www.ux1.eiu.edu/~cfadd/1360/28DC/Loop.html
- http://higheredbcs.wiley.com/legacy/college/cutnell/0470223553/concept_sims/sim34/sim34.html
- http://www.falstad.com/circuit/
- https://www.britannica.com/biography/Gustav-Robert-Kirchhoff
- Schuster, D. (Producer). (2013). Kirchhoff's Loop and Junction Rules Theory [Motion picture]. United States of America: YouTube.
- Schuster, D. (Producer). (2013). Kirchhoff's Rules (Laws) Worked Example [Motion picture]. United States of America: YouTube.
- Anderson, P. (Producer). (2015). Kirchoff's Loop Rule [Motion picture]. United States of America: YouTube.