Charged Spherical Shell
The Main Idea
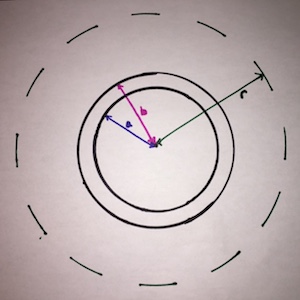
A charged spherical shell is referring to the idea that there is a solid object that can be defined as the space between two concentric spheres that has a uniformly distributed charge, in other words, a hollow sphere that has some thickness. Charged objects create electric fields and this electric field depends on the object's shape, charge, and the distance to the observation location. In the case of a charged spherical shell, if the observation location is within the hollow portion of the shell (distance less than the inner radius of the spherical shell) the electric field is zero. If the observation location is outside of the shell (distance greater than the outer radius of the sphere) then the equation to calculate the electric field of a point charge can be applied. If the observation location is within the spherical shell itself (distance r between inner radius a and outer radius b) then the electric field of the shell can be found using the charge contained within the radius r instead of the total charge.
A Mathematical Model
When considering how to calculate the electric field of a charged spherical shell you first need to identify where the observation location is, and then follow the guidelines below.
Observation location outside of the spherical shell: [math]\displaystyle{ \vec{E}_{sphere}=\frac{1}{4\pi E_0}\frac{Q}{r^2}\widehat{r} }[/math]
Observation location within the spherical shell: [math]\displaystyle{ \vec{E}_{sphere} = \frac{1}{4\pi\epsilon_0}\frac{Q_1}{r^2}\widehat{r} }[/math] where [math]\displaystyle{ Q_1 = \frac{r^3-a^3}{b^3-a^3}Q\widehat{r} }[/math]
Observation location inside of the hollow portion of the spherical shell: [math]\displaystyle{ \vec{E}_{sphere}=0 }[/math]
A Computational Model
Linked below is a VPython simulation of the electric field of a charged spherical shell. The sphere is modeled in this simulation as a series of rings stacked on top of one another with varying radii. The white arrows represent the electric field at any given point, and the yellow trail represents the theoretical path of an electron orbiting the sphere.
Observation Location Outside the Spherical Shell:
If the observation location is outside of the shell, the electric field produced mirrors that of a point charge, due to the shape and charge distribution of the charged spherical shell. Say the shell is located at the origin, and the observation location is on the x-axis. The direction of the electric field produced by the shell at the observation location is in the x direction. This is because all of the other electric field vectors with y and x components cancel out in the y direction, leaving only the electric field in the x direction. The same logic would be used if the observation location was on any of the axes. For example, if the observation location had a unit vector of <1,1,0>, then the electric field would have components in the x and y directions, and their magnitudes would be whatever the value of the electric field was found to be multiplied by 1, since both the x and y components of the unit vector have values of 1.
See this trinket for an example of an electric field of a spherical shell with observation locations outside of the shell.
The idea that the electric field produced by a spherical shell can be modeled with a point charge can be explained through Gauss's Law. Gauss's Law allows one to find the electric field for symmetric charge distributions. Gauss's Law states [math]\displaystyle{ \frac{Q_{enclosed}}{\varepsilon_0} = \oint_C E\bullet dA }[/math].
Gauss's Law considers electric flux through the surface, in which the Electric Field is perpendicular to surface. Therefore, any Electric Field that is tangential to the surface is not considered when determining the charge on a spherical shell.
If a sphere of a radius equal to the distance between the observation location and the center of the shell is used for the gaussian surface,then the area can be replaced as follows: [math]\displaystyle{ E = \frac{Q_{enclosed}}{\varepsilon_0 4\pi r^2} }[/math].
In other words, [math]\displaystyle{ E = \frac{1}{ 4\pi \varepsilon_0} \frac{Q_{enclosed}}{r^2} }[/math] which is the equation for an electric field of a charged particle.
Observation Location Inside the Hollow Portion of the Spherical Shell:
If the observation location is anywhere inside of the spherical shell, then the electric field is zero. If there are positive charges distributed equally around a spherical shell, then those charges contribute to the net electric field. Suppose we choose a point inside the sphere, point A. The contributions of the different charges in the spherical shell cancel each other out. The closer a charge is to point A inside the sphere, the larger its contribution to the electric field at point A. This is because

the distance from an observation location to a charge (r) is inversely proportional to the magnitude of the electric field the charge produces. If point A is closer to one side of the sphere, then that means there are more charges on the other side of the sphere that affect the observation location. The extra magnitude from the greater number of charges on the far side cancel out the increased magnitude of the close side. This causes the electric field to be zero at point A inside the sphere, and this can be generalized to any point inside the sphere.
This concept can also be shown through Gauss's Law.
[math]\displaystyle{ \frac{Q_{enclosed}}{\varepsilon_0} = \oint_C E\bullet dA }[/math]
Using a gaussian surface of a sphere of radius r where r<a<b
the charge enclosed by the gaussian surface is 0, [math]\displaystyle{ 0 = \oint_C E\bullet dA }[/math] and thus the electric field through the surface is also 0.
IMPORTANT: It is very important to remember that the electric field inside a spherical shell is NOT always zero. Other charges that exist may contribute to the electric field inside the spherical shell, only the electric field that is being caused by the uniformly distributed charges within the spherical shell is zero.
Observation Location Within the Spherical Shell:
The electric field at an observation location within the spherical shell itself is dependent on the portion of the shell that is closer to the center of the shell than the observation location. In other words, the electric field is dependent on the distance from the observation location to the center of the spherical shell, the outer radius of the shell, and the inner radius of the shell.

If there is a uniformly charged spherical shell of total charge Q with an outer radius of b, an inner radius of a, the electric field at an observation location radius r away from the center of the shell (a<r<b) can be found as follows:
The charge contained within radius r: [math]\displaystyle{ Q_1 = \frac{r^3-a^3}{b^3-a^3}Q }[/math]
Using Gauss's Law the electric field through the gaussian surface (a sphere of radius r):
[math]\displaystyle{ E = \frac{Q_1}{\epsilon_0*4\pi r^2} }[/math]
There is no electric field contributed by the portion of the shell that is of a radius greater than r, as the observation location would then be inside the hollow section of this larger shell and the electric field would be 0. Thus the electric field at the observation location is only due to the portion of the shell that is less than a distance r away from the center of the shell.
Examples
Simple
A spherical shell of charge with a radius of 5 is located at the origin and is uniformly charged with q=+2. What is the electric field produced from the spherical shell at x=2?
Remember that the electric field is zero withing the hollow center of the shell: [math]\displaystyle{ E = 0 }[/math].
Middling
A spherical shell with a radius of 1m is located at the origin and is uniformly charged with q=+6e-8. What is the electric field produced from the spherical shell at (6,3,2)?
[math]\displaystyle{ E_{sphere} = \frac{1}{4\pi \epsilon_0}\frac{q}{r^2}\widehat{r} }[/math]
[math]\displaystyle{ E_{sphere} = \frac{1}{4\pi \epsilon_0}\frac{6*10^{-8}}{7^2}\lt \frac{6}{7},\frac{3}{7},\frac{2}{7}\gt }[/math]
[math]\displaystyle{ E_{sphere} ≈\ (11.02)\lt \frac{6}{7},\frac{3}{7},\frac{2}{7}\gt }[/math]
Difficult
A spherical shell of charge Q = +5e-10 with an outer radius of 1m and an inner radius of .8m is located at the origin and uniformly charged. What is the electric field produced by the spherical shell at (.9,0,0)?
[math]\displaystyle{ \vec{E}_{sphere} = \frac{1}{4\pi\epsilon_0}\frac{Q_1}{r^2} }[/math] where [math]\displaystyle{ Q_1 = \frac{r^3-a^3}{b^3-a^3}Q }[/math]
[math]\displaystyle{ Q_1 = \frac{.9^3-.8^3}{1^3-.8^3}((5)10^{-10}) }[/math]
[math]\displaystyle{ \vec{E}_{sphere} = \frac{1}{4\pi\epsilon_0}\frac{\frac{.9^3-.8^3}{1^3-.8^3}(5*10^{-10})}{.9^2} }[/math]
[math]\displaystyle{ E_{sphere} ≈\ \lt 2.74489,0,0\gt }[/math]
Step Problem
A conducting spherical shell has an inner radius of a, outer radius of b (a<r<b). It also has a positive point charge of +Q at the center. The total charge on the shell is -4Q.
Find: (1) Electric Field r >b from center. (2) Surface Charge Density on the Inner Surface (3) Surface Charge Density on the Outer Surface
(1)Since this is a conducting shell the Electric Field is pointing inward then the sign is negative. Also the net charge is -4Q+Q=-3Q, this value replaces Q enclosed in the aforementioned section, Computational Model - Outside of the Shell. Therefore the the Electric Field can be noted as: [math]\displaystyle{ E = \frac{-1}{ 4\pi \varepsilon_0} \frac{3*Q_{enclosed}}{r^2} }[/math]
(2)Surface density is the ratio of surface charge to the surface area of the shell, which is a circle. Therefore the surface charge density for the inner surface of a shell can be noted as (using only charge on inside, -Q): [math]\displaystyle{ E = \frac{-Q_{(inner)}}{4\pi{r^2}} }[/math]
(2)The surface charge density for the outer surface of a shell can be noted as (using net, -3Q): [math]\displaystyle{ E = \frac{-3Q_{(inner)}}{4\pi{r^2}} }[/math].
Connectedness
This topic is related to electric fields and the effects that electric fields can have on other objects. For example, electric fields can have effects on humans! The body's voltage can be increased, currents can be induced by the body, and electric charges can buildup on the surface of peoples' skin which is why they feel a tingling sensation when exposed to electric fields (such as from standing under a high voltage power line). This tingling is felt starting from voltages of 1,000 volts per meter. At that same voltage, there are microdischarges when a person touches something made of metal.
This topic is also very closely tied to Gauss's Law as can be seen in the computational model. The electric field can always be found by using Gauss's Law and the charge contained within a certain radius.
History
The electric field from a point charge was discovered by Charles Augustin de Coulomb, a French physicists. Coulomb's law was published in 1784. The law states that the electric field from a point charge is inversely proportional to the distance between the charged particle and the observation location. It also states that if the charge creating the electric field is positive, then the electric field will point radially outward. However, if the particle creating the field is negatively charged, then the electric field will point radially inward.
See also
- Electric Force One application of electric fields due to point charges deals with finding electric force
- Electric Field More general ideas about electric fields
- Gauss's Law More information behind why Gauss's law works and why it can be applied to spherical shells
Further reading
- Principles of Electrodynamics by Melvin Schwartz, ISBN: 9780486134673
External links
References
- Note: all images are original and were produced by the author