Quantum Harmonic Oscillator: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
The Quantum Harmonic Oscillator is the quantum parallel to the classical simple harmonic oscillator. The key difference between these two is in the name. In the quantum harmonic oscillator, energy levels are ''quantized'' meaning there are discrete energy levels to this oscillator, (it cannot be any positive value as a classical oscillator can have). At low levels of energy, an oscillator obeys the rules of quantum mechanics. So the QHO has numerous applications such as molecular vibrations. These energy levels, denoted by <math>E_n, n=1,2,3... </math> and is evaluated by the relation: <br><math> E_n=(n+\frac{1}{2})\hbar\omega </math><br> | The Quantum Harmonic Oscillator is the quantum parallel to the classical simple harmonic oscillator. The key difference between these two is in the name. In the quantum harmonic oscillator, energy levels are ''quantized'' meaning there are discrete energy levels to this oscillator, (it cannot be any positive value as a classical oscillator can have). At low levels of energy, an oscillator obeys the rules of quantum mechanics. So the QHO has numerous applications such as molecular vibrations. These energy levels, denoted by <math>E_n, n=1,2,3... </math> and is evaluated by the relation: <br><math> E_n=(n+\frac{1}{2})\hbar\omega </math><br> | ||
Where <math>n</math> is the principle quantum number, <math>\hbar</math> is the reduced planks constant, and <math>\omega</math> is the angular frequency of the oscillator.<br><br> | Where <math>n</math> is the principle quantum number, <math>\hbar</math> is the reduced planks constant, and <math>\omega</math> is the angular frequency of the oscillator.<br> | ||
[[File:qho2.png|300px|]]<br> | |||
Displayed above is a diagram displaying the quantized energy levels for the quantum harmonic oscillator. | |||
==Comparing the Classic and Quantum== | ==Comparing the Classic and Quantum== | ||
Below is a comparison of the positional probabilities of the classical and quantum harmonic oscillators for the principal quantum number <math>n=3</math><br><br> | Below is a comparison of the positional probabilities of the classical and quantum harmonic oscillators for the principal quantum number <math>n=3</math><br><br> | ||
[[File:Qhm2.png|300px|]]<br> | [[File:Qhm2.png|300px|]]<br> | ||
As <math>n</math> increases, there is more agreement between models. One thing that is interesting to note is that the classical probability is constrained within the dotted lines, as there is a physical limit to the displacement. There is no energy for the displacement of a classical harmonic oscillator to pass the forbidden zone. In the quantum realm, however, recall that there is some probability that the position exceeds these realms as there is some uncertainty given by the Uncertainty Principle. Another notable difference between the two is their differing ground-state energy levels. Classically the minimum energy is simply zero. For the QHO, recall from the introductory section that <br> <math>E_n=(n+\frac{1}{2})\hbar\omega</math>.<br> If <math>n=0</math>, then by substitution we see that <math>E_0=\frac{\hbar\omega}{2}</math><br><br> | As <math>n</math> increases, there is more agreement between models. One thing that is interesting to note is that the classical probability is constrained within the dotted lines, as there is a physical limit to the displacement. There is no energy for the displacement of a classical harmonic oscillator to pass the forbidden zone. In the quantum realm, however, recall that there is some probability that the position exceeds these realms as there is some uncertainty given by the Uncertainty Principle. Another notable difference between the two is their differing ground-state energy levels. Classically the minimum energy is simply zero. For the QHO, recall from the introductory section that the diagram doesn't have an energy level at zero and that <br> <math>E_n=(n+\frac{1}{2})\hbar\omega</math>.<br> If <math>n=0</math>, then by substitution we see that <math>E_0=\frac{\hbar\omega}{2}</math><br><br> | ||
This is intuitively logical as <math>E_0=0</math> is contradictory to Heisenberg's Uncertainty Principle. If the ground state energy were to be zero, the given particle would be motionless. If the particle is motionless, then <br><br><math>p=0</math> and <math> x=C </math>. Since this hypothetical particle has invariant momentum and position, then <math>\Delta x=0</math> and <math>\Delta p=0</math> which directly violates <math>\Delta p \Delta x \geq \frac{\hbar}{2}</math> | This is intuitively logical as <math>E_0=0</math> is contradictory to Heisenberg's Uncertainty Principle. If the ground state energy were to be zero, the given particle would be motionless. If the particle is motionless, then <br><br><math>p=0</math> and <math> x=C </math>. Since this hypothetical particle has invariant momentum and position, then <math>\Delta x=0</math> and <math>\Delta p=0</math> which directly violates <math>\Delta p \Delta x \geq \frac{\hbar}{2}</math><br> | ||
==Potential for Analytical, Closed-Form Solution to the Schrodinger Equation for the Quantum Harmonic Oscillator== | |||
The quantum harmonic oscillator is one of the few systems modeled by the Schrodinger Equation that has an analytical solution. We will make an attempt to derive the solution in one spacial dimension:<br> | |||
Revision as of 10:04, 6 December 2022
The Quantum Harmonic Oscillator is the quantum parallel to the classical simple harmonic oscillator. The key difference between these two is in the name. In the quantum harmonic oscillator, energy levels are quantized meaning there are discrete energy levels to this oscillator, (it cannot be any positive value as a classical oscillator can have). At low levels of energy, an oscillator obeys the rules of quantum mechanics. So the QHO has numerous applications such as molecular vibrations. These energy levels, denoted by [math]\displaystyle{ E_n, n=1,2,3... }[/math] and is evaluated by the relation:
[math]\displaystyle{ E_n=(n+\frac{1}{2})\hbar\omega }[/math]
Where [math]\displaystyle{ n }[/math] is the principle quantum number, [math]\displaystyle{ \hbar }[/math] is the reduced planks constant, and [math]\displaystyle{ \omega }[/math] is the angular frequency of the oscillator.
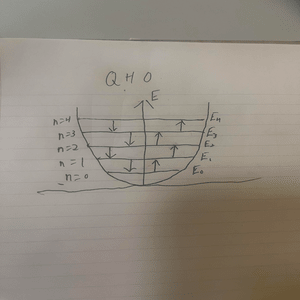
Displayed above is a diagram displaying the quantized energy levels for the quantum harmonic oscillator.
Comparing the Classic and Quantum
Below is a comparison of the positional probabilities of the classical and quantum harmonic oscillators for the principal quantum number [math]\displaystyle{ n=3 }[/math]
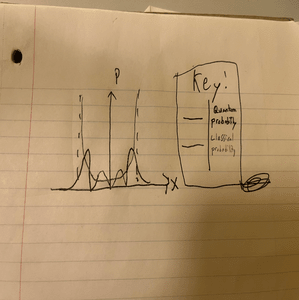
As [math]\displaystyle{ n }[/math] increases, there is more agreement between models. One thing that is interesting to note is that the classical probability is constrained within the dotted lines, as there is a physical limit to the displacement. There is no energy for the displacement of a classical harmonic oscillator to pass the forbidden zone. In the quantum realm, however, recall that there is some probability that the position exceeds these realms as there is some uncertainty given by the Uncertainty Principle. Another notable difference between the two is their differing ground-state energy levels. Classically the minimum energy is simply zero. For the QHO, recall from the introductory section that the diagram doesn't have an energy level at zero and that
[math]\displaystyle{ E_n=(n+\frac{1}{2})\hbar\omega }[/math].
If [math]\displaystyle{ n=0 }[/math], then by substitution we see that [math]\displaystyle{ E_0=\frac{\hbar\omega}{2} }[/math]
This is intuitively logical as [math]\displaystyle{ E_0=0 }[/math] is contradictory to Heisenberg's Uncertainty Principle. If the ground state energy were to be zero, the given particle would be motionless. If the particle is motionless, then
[math]\displaystyle{ p=0 }[/math] and [math]\displaystyle{ x=C }[/math]. Since this hypothetical particle has invariant momentum and position, then [math]\displaystyle{ \Delta x=0 }[/math] and [math]\displaystyle{ \Delta p=0 }[/math] which directly violates [math]\displaystyle{ \Delta p \Delta x \geq \frac{\hbar}{2} }[/math]
Potential for Analytical, Closed-Form Solution to the Schrodinger Equation for the Quantum Harmonic Oscillator
The quantum harmonic oscillator is one of the few systems modeled by the Schrodinger Equation that has an analytical solution. We will make an attempt to derive the solution in one spacial dimension: