Quantum Harmonic Oscillator

Claimed - Eric Carder Fall 2022
The Quantum Harmonic Oscillator is the quantum parallel to the classical simple harmonic oscillator. The key difference between these two is in the name. In the quantum harmonic oscillator, energy levels are quantized meaning there are discrete energy levels to this oscillator, (it cannot be any positive value as a classical oscillator can have). At low levels of energy, an oscillator obeys the rules of quantum mechanics. The QHO does have applications, most notably as an approximation of molecular vibrations. These energy levels, denoted by [math]\displaystyle{ E_n, n=1,2,3... }[/math] can be evaluated by the relation:
[math]\displaystyle{ E_n=(n+\frac{1}{2})\hbar\omega }[/math]
Where [math]\displaystyle{ n }[/math] is the principal quantum number, [math]\displaystyle{ \hbar }[/math] is the reduced planks constant, and [math]\displaystyle{ \omega }[/math] is the angular frequency of the oscillator.

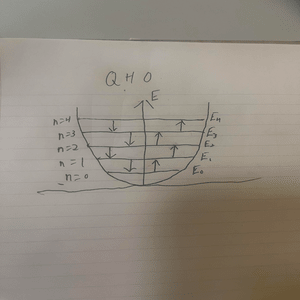
Displayed above is a diagram displaying the quantized energy levels for the quantum harmonic oscillator.

Comparing the Classic and Quantum

Below is a comparison of the positional probabilities of the classical and quantum harmonic oscillators for the principal quantum number [math]\displaystyle{ n=3 }[/math]


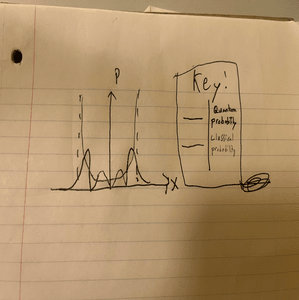
As [math]\displaystyle{ n }[/math] increases, there is more agreement between models. One thing that is interesting to note is that the classical probability is constrained within the dotted lines, as there is a physical limit to the displacement. There is no energy for the displacement of a classical harmonic oscillator to pass the forbidden zone. In the quantum realm, however, recall that there is some probability that the position exceeds these realms as there is some uncertainty given by the Uncertainty Principle. Another notable difference between the two is their differing ground-state energy levels. Classically the minimum energy is simply zero. For the QHO, recall from the introductory section that the diagram doesn't have an energy level at zero and that

[math]\displaystyle{ E_n=(n+\frac{1}{2})\hbar\omega }[/math].

If [math]\displaystyle{ n=0 }[/math],

then by substitution, we see that

[math]\displaystyle{ E_0=\frac{\hbar\omega}{2} }[/math]

This is logical as [math]\displaystyle{ E_0=0 }[/math] is contradictory to Heisenberg's Uncertainty Principle. If the ground state energy were to be zero, the given particle would be motionless. If the particle is motionless, then

[math]\displaystyle{ p=0 }[/math] and [math]\displaystyle{ x=C }[/math]. Since this hypothetical particle has invariant momentum and position, then [math]\displaystyle{ \Delta x=0 }[/math] and [math]\displaystyle{ \Delta p=0 }[/math] which directly violates [math]\displaystyle{ \Delta p \Delta x \geq \frac{\hbar}{2} }[/math]

Proving the Ground-State Energy Relation Using Uncertainty Principle

The Uncertainty Principle mathematically limits the ground-state energy level to [math]\displaystyle{ E_0=\frac{\hbar\omega}{2} }[/math].
The classical definition of kinetic energy is: [math]\displaystyle{ KE=\frac{1}{2}mv^2 }[/math]
Rewriting in terms of momentum is: [math]\displaystyle{ KE= \frac{p^2}{2m} }[/math]
Classically, we know the spring potential for the SHO: [math]\displaystyle{ U(x)=\frac{1}{2}kx^2 }[/math]
We also know the angular frequency is: [math]\displaystyle{ \omega=\sqrt{\frac{k}{m}} }[/math]

In solving for [math]\displaystyle{ k }[/math], we get [math]\displaystyle{ k=\omega^2m }[/math]

Rewrite the potential as:

[math]\displaystyle{ U(x)=\frac{1}{2}mx^2\omega^2 }[/math]

In formulating in terms of uncertainties, the energy for the QHO must be at least:

[math]\displaystyle{ E=\frac{(\Delta p)^2}{2m} + \frac{1}{2}m\omega^2 (\Delta x)^2 }[/math]

In considering the lower bound of the Uncertainty Principle, namely when the relationship is equal such that:
[math]\displaystyle{ \Delta x \Delta p = \frac{\hbar}{2} }[/math]

We can rewrite one uncertainty as a function of the other. In this case, we will rewrite the momentum uncertainty as a function of the position uncertainty:

[math]\displaystyle{ \Delta p = \frac{\hbar}{2\Delta x} }[/math] and substituting into the energy relation

[math]\displaystyle{ E=\frac{\hbar^2}{8m(\Delta x)^2} + \frac{1}{2}m\omega^2 (\Delta x)^2 }[/math]

Our goal is to minimize the energy, hence we now differentiate and set it to zero to find the critical point.
[math]\displaystyle{ \frac{d}{d(\Delta x)}\bigg[ E=\frac{\hbar^2}{8m(\Delta x)^2} + \frac{1}{2}m\omega^2 (\Delta x)^2 \bigg] = -\frac{\hbar^2}{4m(\Delta x)^3} + m\omega^2 \Delta x =0 }[/math]

Solving for [math]\displaystyle{ \Delta x }[/math] yields:
[math]\displaystyle{ \Delta x = \sqrt{\frac{\hbar}{2m\omega}} }[/math]

All that remains now is to substitute the derived positional uncertainty into the Energy equation:

[math]\displaystyle{ E=\frac{\hbar^2}{8m(\Delta x)^2} + \frac{1}{2}m\omega^2 (\Delta x)^2 }[/math]

[math]\displaystyle{ E_0=\frac{\hbar^2}{8m(\sqrt{\frac{\hbar}{2m\omega}})^2} + \frac{1}{2}m\omega^2 (\sqrt{\frac{\hbar}{2m\omega}})^2 }[/math]

[math]\displaystyle{ E_0=\frac{2m\omega \hbar}{8m\hbar} + \frac{1}{2}m\omega^2 (\sqrt{\frac{\hbar}{2m\omega}})^2 }[/math]

[math]\displaystyle{ E_0=\frac{\hbar \omega}{4} + \frac{\hbar \omega}{4} }[/math]

[math]\displaystyle{ \therefore E_0 = \frac{\hbar \omega}{2} }[/math]
This is substantial as it proves that, unlike the classical harmonic oscillator, the quantum harmonic oscillator cannot have zero energy. This holds true even in the absence of any temperature. So in the modeling of polyatomic molecules in a gas, they still must have energy even at absolute zero. The ground-vibrational state energy is generally referred to as "zero point vibration"

Deriving the Energy and Considering the Potential for Analytical, Closed-Form Solutions

The quantum harmonic oscillator is one of the few systems modeled by the Schrodinger Equation that has an analytical solution. The solution requires many unintuitive substitutions that would be difficult to spontaneously arrive at. We will make an attempt to derive the formula for energy in one spacial dimension using spectral analysis:

Rewriting the potential that we derived above previously as:

[math]\displaystyle{ U(x)=\frac{1}{2}mx^2\omega^2 }[/math]

The one-dimensional, time-dependent Schrodinger Equation is:

[math]\displaystyle{ \frac{-\hbar^2}{2m}\frac{d^2\Psi}{dx^2}+U(x)\Psi=E\Psi }[/math]

In substituting our derived potential:

[math]\displaystyle{ \frac{-\hbar^2}{2m}\frac{d^2\Psi}{dx^2}+\frac{1}{2}mx^2\omega^2\Psi=E\Psi }[/math]

Dividing both sides by [math]\displaystyle{ \frac{-\hbar^2}{2m} }[/math] and setting the differential equation equal to zero yields:

[math]\displaystyle{ \frac{d^2\Psi}{dx^2}+(\frac{2mE}{\hbar^2}-\frac{m^2\omega^2 x^2}{\hbar^2})\Psi=0 }[/math]

We will soon use a power series to simplify the equation. First, let's assign a dimensionless variable:

[math]\displaystyle{ t=x\sqrt{\frac{m\omega}{\hbar}} }[/math]
Substituting into our main equation now gives:

[math]\displaystyle{ \frac{d^2\Psi}{dt^2}+\Psi(t)(\frac{2E}{\hbar\omega}-t^2)=0 }[/math]

The [math]\displaystyle{ \frac{2E}{\hbar\omega} }[/math] is negligible for large [math]\displaystyle{ t }[/math] values Hence we use the guessing method to solve this second-order differential equation.

The wave function should include [math]\displaystyle{ e^{\frac{-t^2}{2}} }[/math]

So let's guess a solution of the form: [math]\displaystyle{ \Psi(t)=u(t)e^{\frac{-t^2}{2}} }[/math]

Now of course we must differentiate and substitute into the differential equation.

[math]\displaystyle{ \frac{d\Psi(t)}{dt}=\frac{du(t)}{dt}e^{\frac{-t^2}{2}}-tu(t)e^{\frac{-t^2}{2}} }[/math]

[math]\displaystyle{ \frac{d^2\Psi(t)}{dt^2}=\frac{d^2u(t)}{dt^2}e^{\frac{-t^2}{2}}-t\frac{du(t)}{dt}e^{\frac{-t^2}{2}}-t\frac{du(t)}{dt}e^{\frac{-t^2}{2}}+u(t)(t^2-1)e^{\frac{-t^2}{2}}. }[/math]

Time to substitute the derivatives: [math]\displaystyle{ \frac{d^2u(t)}{dt^2}e^{\frac{-t^2}{2}}-2t\frac{du(t)}{dt}+u(t)(t^2-1)e^{\frac{-t^2}{2}}+(\frac{2E}{\hbar\omega}-t^2)u(t)e^{\frac{-t^2}{2}}=0 }[/math]

Which simplifies quite nicely:

[math]\displaystyle{ \frac{d^2u(t)}{dt^2}e^{\frac{-t^2}{2}}-2t\frac{du(t)}{dt}-u(t)e^{\frac{-t^2}{2}}+\frac{2E}{\hbar\omega}u(t)e^{\frac{-t^2}{2}}=0 }[/math]

Now we omit [math]\displaystyle{ e^{\frac{-t^2}{2}} }[/math] by dividing both sides by the expression:

[math]\displaystyle{ \frac{d^2u(t)}{dt^2}-2t\frac{du(t)}{dt}-u(t)+(\frac{2E}{\hbar\omega}-1)u(t)=0 }[/math]

We can now construct a power series to find a direct solution:

[math]\displaystyle{ u(t)=\sum_{n=0}^\infty{a_nt^n} }[/math]

Now we repeat the above process of differentiation and substitution:

[math]\displaystyle{ \frac{du(t)}{dt}=\sum_{n=0}^\infty{na_nt^{n-1}} }[/math]

[math]\displaystyle{ \frac{d^2u(t)}{dt^2}=\sum_{n=0}^\infty{(n-1)na_nt^{n-2}} }[/math]

Once again we substitute and unintuitively replace [math]\displaystyle{ n }[/math] with [math]\displaystyle{ n+2 }[/math]

To show how this works, here is an expansion of [math]\displaystyle{ u(t) }[/math]:

[math]\displaystyle{ u(t)=a_0+a_1t+a_2t^2+a_3t^3... }[/math]

By inspection (evaluate if you'd like), differentiating [math]\displaystyle{ u(t) }[/math] twice yields zero for the first two terms.

[math]\displaystyle{ \sum_{n=0}^\infty{((n+2)-1))a_{n+2}t^{(n+2)-2}+(\frac{2E}{\hbar\omega}-1-2n)\sum_{n=0}^\infty{a_nt^n}}=0 }[/math]

In simplifying again: [math]\displaystyle{ \sum_{n=0}^\infty{\bigg[(n+2)(n+1)a_{n+2}+(\frac{2E}{\hbar\omega}-1-2n)a_n)\bigg]t^{2n}}=0 }[/math]

Notice that the RHS of the equation above is equal to zero. This means that the coefficient of [math]\displaystyle{ t^{2n} }[/math] equals zero. Hence we can make the following equation and solve for [math]\displaystyle{ a_{n+2} }[/math]

[math]\displaystyle{ (n+2)(n+1)a_{n+2}+(\frac{2E}{\hbar \omega}-1-2n)a_n=0 }[/math]

[math]\displaystyle{ a_{n+2}=\frac{2n+1-\frac{2E}{\hbar\omega}}{(n+1)(n+2)}a_n }[/math]

Since [math]\displaystyle{ \frac{2}{n} }[/math] decreases faster than [math]\displaystyle{ e^{\frac{-t^2}{2}} }[/math], we must equate the numerator of [math]\displaystyle{ a_{n+2} }[/math] to zero in order to avoid divergence.:

[math]\displaystyle{ 2n+1-\frac{2E}{\hbar\omega}=0 }[/math]

Algebraically solving for [math]\displaystyle{ E }[/math] yields:

[math]\displaystyle{ E=\frac{\hbar\omega}{2}(2n+1)=(n+\frac{1}{2})\hbar\omega }[/math]

Which is the energy formula as seen in the introduction.

Deriving a closed-form solution for the wave function is more difficult, and requires the inclusion of Hermite Polynomials. The one dimensional solution is:

: [math]\displaystyle{ \Psi(x)=H_n(\frac{m\omega}{\pi\hbar})^{\frac{1}{4}}\cdot\frac{1}{\sqrt{2^nn!}}\bigg[\bigg(\frac{m\omega}{\hbar}\bigg)^\frac{1}{2}x\bigg]e^\frac{-m\omega x^2}{2\hbar} }[/math]

Where [math]\displaystyle{ H_n }[/math] are Hermite Polynomials defined as:

[math]\displaystyle{ H_n(x)=(-1)^ne^{x^2}\cdot \frac{d^n }{d x^n}e^{-x^2} }[/math]

History

In the case of the quantum harmonic oscillator, there isn't much history for it. It is more so a specific case of the Schrodinger Equation, as it was one of the first cases solved after the famous equation was formulated. The first solution of the QHO I've been able to find was as early as 1925, in a paper written by Max Born and Pascual Jordan.

Connectedness

At first glance, applications of the quantum harmonic oscillator seem limited. It's important to realize that it is simply an analog of its classical counterpart. When harmonically oscillating systems approach the atomic scale, they must obey the laws of quantum mechanics as anything else would. An adept understanding of quantum harmonic oscillators can enhance humans' understanding of larger-scale models. A quick example would be the consideration of how an understanding of molecular vibrations can lead to a greater understanding of the phenomena that are byproducts of these vibrations.

References

Dudik, R. (2004, May 5). The Quantum Harmonic Oscillator. Retrieved 2022, from http://physics.gmu.edu/~dmaria/590%20Web%20Page/public_html/qm_topics/harmonic/

Libretexts. (2020, August 11). 5.6: The harmonic-oscillator wavefunctions involve hermite polynomials. Chemistry LibreTexts. Retrieved 2022, from https://chem.libretexts.org/Courses/Pacific_Union_College/Quantum_Chemistry/05%3A_The_Harmonic_Oscillator_and_the_Rigid_Rotor/5.06%3A_The_Harmonic-Oscillator_Wavefunctions_involve_Hermite_Polynomials

Libretexts. (2022, September 12). 7.6: The Quantum Harmonic Oscillator. Physics LibreTexts. Retrieved 2022, from https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/University_Physics_III_-_Optics_and_Modern_Physics_(OpenStax)/07%3A_Quantum_Mechanics/7.06%3A_The_Quantum_Harmonic_Oscillator

Born, Max; Jordan, Pascual, Zur Quantenmechanik, Z. f. Physik 34, 858-888 (1925). ZBL51.0728.08. (27 September 1925)

Nave, R. (2014). Energy minimum from uncertainty principle. Quantum Harmonic Oscillator. Retrieved 2022, from http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hosc4.html#c1