Magnetic Field of a Disk: Difference between revisions
No edit summary |
|||
| Line 1: | Line 1: | ||
==Main Idea== | ==Main Idea== | ||
Through this page, you will understand how to solve for the magnetic field produced by a | Through this page, you will understand how to solve for the magnetic field produced by a rotating, charged, circular disk. | ||
First, let us start with the basics. We know that moving charges spread out over the surface of an object will produce a magnetic field. This is similar to the concept of how charges spread out over an object allowed them to produce unique electric fields. | First, let us start with the basics. We know that moving charges spread out over the surface of an object will produce a magnetic field. This is similar to the concept of how charges spread out over an object allowed them to produce unique electric fields. | ||
| Line 7: | Line 7: | ||
===Mathematical Model=== | ===Mathematical Model=== | ||
Say we have a flat circular disk with radius <math>R</math> and carrying a uniform surface charge density <math>\sigma</math>. It rotates with an angular velocity <math>\omega</math> about the z-axis. | Say we have a "flat" circular disk with radius <math>R</math> and carrying a uniform surface charge density <math>\sigma</math>. It rotates with an angular velocity <math>\omega</math> about the z-axis. | ||
[[File:magfielddisk1.png|400px|center]] | [[File:magfielddisk1.png|400px|center]] | ||
To find the magnetic field <math>B</math> at any point <math>z</math> along the rotation axis, we can consider the disk to be a collection of concentric current loops. Breaking the disk into a series of loops with infinitesimal width <math>dr</math> and with radius <math>r</math>, we will have | To find the magnetic field <math>B</math> at any point <math>z</math> along the rotation axis, we can consider the disk to be a collection of concentric current loops. Breaking the disk into a series of loops with infinitesimal width <math>dr</math> and with radius <math>r</math>, we will have an infinitesimal area for loop : | ||
<math>dA = 2\pi r dr</math> | ::<math>dA = 2\pi r dr </math>, where | ||
:::<math>A = \pi r^2</math> | |||
<math>dQ = 2\pi \sigma rdr</math> | And therefore have an infinitesimal charge on each loop of: | ||
::<math>dQ = 2\pi \sigma rdr</math>, where | |||
:::<math>Q = \sigma A</math> | |||
This loop is rotating at an angular velocity <math>\omega</math>, which means the charge <math>dQ</math> on our loop makes a full rotation around the axis every period, | This loop is rotating at an angular velocity <math>\omega</math>, which means the charge <math>dQ</math> on our loop makes a full rotation around the axis every period, | ||
<math> T = \frac{2\pi}{\omega} </math> seconds. | ::<math> T = \frac{2\pi}{\omega} </math> seconds. | ||
Since a charge <math>dQ</math> makes a full rotation every <math>T</math> seconds, our infinitesimally thin ring is a current loop with an infinitesimal current: | |||
::<math>dI = \frac{dQ}{T} = \frac{2\pi \sigma rdr}{\frac{2\pi}{\omega}} = \sigma \omega rdr </math>, where | |||
<math> | :::<math>I = \frac{Q}{t}</math> | ||
For this single loop, equivalent to a current <math>dI</math>, we can calculate the field a distance <math>z</math> above the axis. Using this proof from the Magnetic Field of a Loop page, we can get | For this single loop, equivalent to a current <math>dI</math>, we can calculate the field a distance <math>z</math> above the axis. Using this proof from the [[Magnetic Field of a Loop]] page, we can get: | ||
<math> dB = \frac{\mu_0 r^2 dI}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}}</math> | ::<math> dB = \frac{\mu_0 r^2 dI}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}}</math> | ||
Now to find the total field for all of the concentric rings, we must integrate from <math>r = 0</math> to <math>r = R</math>: | Now to find the total magnetic field for all of the concentric rings, we must integrate from <math>r = 0</math> to <math>r = R</math>: | ||
<math> B = \int_{0}^{R} \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 \sigma\omega}{2} \int_{0}^{R} \frac{r^3 dr}{(r^2+z^2)^{3/2}}</math> | ::<math> B = \int_{0}^{R} \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 \sigma\omega}{2} \int_{0}^{R} \frac{r^3 dr}{(r^2+z^2)^{3/2}}</math> | ||
<math> B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+r^2}{\sqrt{r^2+z^2}}\right]_{0}^{R}</math> | ::<math> B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+r^2}{\sqrt{r^2+z^2}}\right]_{0}^{R}</math> | ||
<math> B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+R^2}{\sqrt{R^2+z^2}} - 2|z| \right]</math> | ::<math> B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+R^2}{\sqrt{R^2+z^2}} - 2|z| \right]</math> | ||
The absolute value around the z is important because we want the field to be the same on either side of the disk, whether in the positive z or negative z direction. | The absolute value around the <math>z</math> is important because we want the field to be the same on either side of the disk, whether we are in the positive z or negative z direction. | ||
===Computational Model=== | ===Computational Model=== | ||
::'''Insert Computational Model here''' | |||
==Examples== | ==Examples== | ||
Revision as of 10:22, 25 August 2019
Main Idea
Through this page, you will understand how to solve for the magnetic field produced by a rotating, charged, circular disk.
First, let us start with the basics. We know that moving charges spread out over the surface of an object will produce a magnetic field. This is similar to the concept of how charges spread out over an object allowed them to produce unique electric fields.
In order to figure out this magnetic field, we will start from the fundamental principles that we have learned already with regards to how magnetic fields are produced. We will then build on that and include the geometry of the object in question, in this a circular disk, in order to solve for the magnetic field produced by this disk.
Mathematical Model
Say we have a "flat" circular disk with radius [math]\displaystyle{ R }[/math] and carrying a uniform surface charge density [math]\displaystyle{ \sigma }[/math]. It rotates with an angular velocity [math]\displaystyle{ \omega }[/math] about the z-axis.
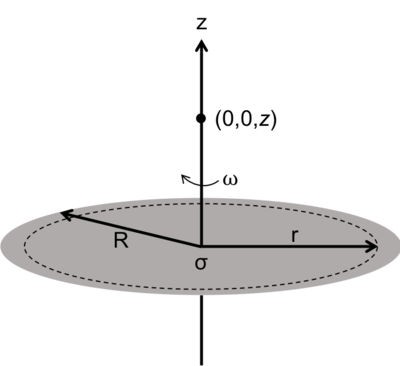
To find the magnetic field [math]\displaystyle{ B }[/math] at any point [math]\displaystyle{ z }[/math] along the rotation axis, we can consider the disk to be a collection of concentric current loops. Breaking the disk into a series of loops with infinitesimal width [math]\displaystyle{ dr }[/math] and with radius [math]\displaystyle{ r }[/math], we will have an infinitesimal area for loop :
- [math]\displaystyle{ dA = 2\pi r dr }[/math], where
- [math]\displaystyle{ A = \pi r^2 }[/math]
And therefore have an infinitesimal charge on each loop of:
- [math]\displaystyle{ dQ = 2\pi \sigma rdr }[/math], where
- [math]\displaystyle{ Q = \sigma A }[/math]
This loop is rotating at an angular velocity [math]\displaystyle{ \omega }[/math], which means the charge [math]\displaystyle{ dQ }[/math] on our loop makes a full rotation around the axis every period,
- [math]\displaystyle{ T = \frac{2\pi}{\omega} }[/math] seconds.
Since a charge [math]\displaystyle{ dQ }[/math] makes a full rotation every [math]\displaystyle{ T }[/math] seconds, our infinitesimally thin ring is a current loop with an infinitesimal current:
- [math]\displaystyle{ dI = \frac{dQ}{T} = \frac{2\pi \sigma rdr}{\frac{2\pi}{\omega}} = \sigma \omega rdr }[/math], where
- [math]\displaystyle{ I = \frac{Q}{t} }[/math]
For this single loop, equivalent to a current [math]\displaystyle{ dI }[/math], we can calculate the field a distance [math]\displaystyle{ z }[/math] above the axis. Using this proof from the Magnetic Field of a Loop page, we can get:
- [math]\displaystyle{ dB = \frac{\mu_0 r^2 dI}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}} }[/math]
Now to find the total magnetic field for all of the concentric rings, we must integrate from [math]\displaystyle{ r = 0 }[/math] to [math]\displaystyle{ r = R }[/math]:
- [math]\displaystyle{ B = \int_{0}^{R} \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 \sigma\omega}{2} \int_{0}^{R} \frac{r^3 dr}{(r^2+z^2)^{3/2}} }[/math]
- [math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+r^2}{\sqrt{r^2+z^2}}\right]_{0}^{R} }[/math]
- [math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+R^2}{\sqrt{R^2+z^2}} - 2|z| \right] }[/math]
The absolute value around the [math]\displaystyle{ z }[/math] is important because we want the field to be the same on either side of the disk, whether we are in the positive z or negative z direction.
Computational Model
- Insert Computational Model here
Examples
Simple
Middling
Difficult
Connectedness
History
See also
Further reading
External links
Magnetic Field of a Long Straight Wire