Field of a Charged Rod: Difference between revisions

From Physics Book
Jump to navigation Jump to search
No edit summary
 
(48 intermediate revisions by 6 users not shown)
Line 1: Line 1:
 
'''Sajan Thomas, Spring 2024'''
''(After finishing this, I found an article called [[Charged Rod]] written by the people of yesteryear. I didn't see that and created this new one instead. The 2 should be merged in the future.)''


== The Main Idea ==
== The Main Idea ==


Previously, we've learned about the electric field of a point particle. Often, when analyzing physical systems, it is the case that we're unable to analyze each individual particle that composes an object and need to therefore generalize collections of particles into shapes (in this case, a rod) whereby the mathematics corresponding to electric field calculations can be simplified. This can essentially be done by adding up the contributions to the electric field made by parts of an object, approximating each part of an object as a point charge.
Previously, we've learned about the electric field of a point particle. While this skill does build the fundamentals of E&M physics, the real world is not simply made up of isolated particles. In fact, the world is consisted of many geometric shapes our one equation for the electric field of a particle cannot account for. One such example of these geometric shapes is a '''rod'''.


Some objects, such as rods, can be modeled as a uniformly charged object in order to calculate the electric field at some observation location. The following wiki page provides an overview of electric fields created by uniformly charged thin rods, briefly presenting its inception, some specific cases, and proof of concept experiments. The case of a uniformly charged thin rod is a fundamental example of electric field patterns and calculations within physics. Its implications can be applied to other charged objects, such as rings, disks, and spheres.
For the purposes of this course's scope, we assume that the charge is uniformly distributed along the rod. This is an important assumption to make since if it weren't the case, a lot of the calculations would change. This in mind, let's start with what we know: the electric field of a point particle. By itself, we can't represent a rod. But, if we stack a lot of charged particles together closely in a line, what do we get? a rod. That is the basis of how we calculate the electric field of a charged rod.  


In practical situations, objects have charges spread all over their surface. When going about calculating the electric fields of these objects, we can either use one of two processes: numerical summation or integration, or dividing an object into many pieces and summing the individual pieces' electric field contributions. As with point charges, the direction of the field is determined by the sign of the object's charge (positive-points away, negative-points toward) and the size of the field is determined by the observation distance and the magnitude of the object's charge.
That's the basis of it but for now, we'll keep that for later when we're actually deriving how to find it. First, let's discuss the factors that can contribute to the electric field of the charged rod. Firstly, as with any electric field, we have to know the charge of the source-- in this case, the rod. Secondly, we have to know the length of the rod. Thirdly, we also should know the observation location to find the radius from the rod.  


The process of finding the electric field due to charge distributed over an object has four steps:
The process of finding the electric field due to charge distributed over an object has four steps:


1. Divide the charged object into small pieces. Make a diagram and draw the electric field <math>\Delta \vec{E}</math> contributed by one of the pieces.
1. Consider the rod, as previously discussed, as a collection of many, many, infinitesimally small charged particles. Make a diagram and draw the electric field <math>\Delta \vec{E}</math> contributed by one of the pieces.


2. Choose an origin and the axes. Write an algebraic expression for the electric field <math>\Delta \vec{E}</math> due to one piece.
2. By drawing the vectors for the <math>\Delta \vec{E}</math> contributed to one piece, and repeating it along the rod, you should realize by symmetry that several of the vector components will cancel out.  


3. Add up the contributions of all pieces, either numerically or symbolically.
3. Add up the contributions of all pieces, either numerically or symbolically. While there is a formula we can just apply simply later, this step requires integration as you are adding all of the <math>\Delta \vec{E}</math> contributions of many, many, charged particles.  


4. Check that the result is physically correct.
4. Check that the result is physically correct.


=== A Mathematical Model (Explaination 1) ===
=== A Mathematical Model ===
The process of calculating a uniformly charged rod's electric field is tedious, but breaking the process down into several steps makes the task at hand easier. Consider a uniformly charged thin rod of length <math>L</math>  and positive charge <math>Q</math> centered on and lying along the x-axis. The rod is being observed from above at a point on the y-axis.
The process of calculating a uniformly charged rod's electric field is tedious, but breaking the process down into several steps makes the task at hand easier. Consider a uniformly charged thin rod of length <math>L</math>  and positive charge <math>Q</math> centered on and lying along the x-axis. The rod is being observed from above at a point on the y-axis.
[[Image:SajanThomas1.png|800px|center|thumb|Figure 2: Problem 2]]


'''Step 1: Divide the Distribution into Pieces; Draw <math>\Delta \vec{E}</math>'''
'''Step 1: Divide the Distribution into Pieces; Draw <math>\Delta \vec{E}</math>'''


Imagine dividing the rod into a series of very thin slices, each with the same charge <math>\Delta Q</math>. This charge <math>\Delta Q</math> is a small part of the overall charge.  Picture it as a point charge.  Each slice contributes its own electric field, <math>\Delta E</math>.  Summing all these individual slices of <math>E</math> gives you the total electric field of the rod.  This process is the same as taking an integral, as each thickness approaches 0 and the the number of slices approaches infinity.  Note that in this example, the variable that is changing for each slice is its x-coordinate.
Imagine dividing the rod into a series of very thin slices, each with the same charge <math>\Delta Q</math>. This charge <math>\Delta Q</math> is a small part of the overall charge.  Picture it as a point charge.  Each slice contributes its own electric field, <math>\Delta E</math>.  Summing all these individual slices of <math>E</math> gives you the total electric field of the rod.  This process approaches taking an integral, as each thickness approaches 0 and the the number of slices approaches infinity.  Note that in this example, the variable that is changing for each slice is its x-coordinate.
 
[[Image:SajanThomas2.png|800px|center|thumb|Figure 2: Problem 2]]
 


'''Step 2: Write an Expression for the Electric Field Due to One Piece'''
'''Step 2: Write an Expression for the Electric Field Due to One Piece'''


The second step is to write a mathematical expression for the field <math>\Delta E</math> contributed by a single slice of the rod.  We use the formula of the electric field for a point charge because we are imagining each slice as a point charge.  First, determine <math>r</math>, the vector pointing from the source to the observation location.  For our example, this is <math> r = obs - source = <0,y,0> - < x,0,0> = <-x,y,0></math>.  Now use this to calculate the magnitude and direction of <math>r</math>.  So <math>|\vec{r}| = \sqrt{(-x)^2 + y^2} = \sqrt{x^2 + y^2}</math> and <math>\hat{r} = \frac{\vec{r}}{\hat{r}} = \frac{< -x,y,0>}{\sqrt{x^2 + y^2}} </math>. <math> \hat{r}</math> is the vector portion of the expression for the field.  The scalar portion is <math> \frac{1}{4\pi\epsilon_0} \cdot \frac{\Delta Q}{|\vec{r}|^2}</math>.  Thus the expression for one slice of the rod is:
The second step is to write a mathematical expression for the field <math>\Delta E</math> contributed by a single slice of the rod.  We use the formula of the electric field for a point charge because we are imagining each slice as a point charge.  First, determine <math>r</math>, the vector pointing from the source to the observation location.  For our example, this is <math> r = obs - source = <0,y,0> - < x,0,0> = <-x,y,0></math>.  Now use this to calculate the magnitude and direction of <math>r</math>.  So <math>|\vec{r}| = \sqrt{(-x)^2 + y^2} = \sqrt{x^2 + y^2}</math> and <math>\hat{r} = \frac{\vec{r}}{\hat{r}} = \frac{< -x,y,0>}{\sqrt{x^2 + y^2}} </math>. <math> \hat{r}</math> is the vector portion of the expression for the field.  The scalar portion is <math> \frac{1}{4\pi\epsilon_0} \cdot \frac{\Delta Q}{|\vec{r}|^2}</math>.  Thus the expression for one slice of the rod is:
<math> \Delta \vec{E} = \frac{1}{4\pi\epsilon_0} \cdot \frac{\Delta Q}{(\sqrt{x^2+y^2})^{3/2}} \cdot < -x,y,0> </math>.
<math> \Delta \vec{E} = \frac{1}{4\pi\epsilon_0} \cdot \frac{\Delta Q}{(x^2+y^2)^{3/2}} \cdot < -x,y,0> </math>.


'''Determining <math>\Delta Q</math> and the integration variable'''
'''Determining <math>\Delta Q</math> and the integration variable'''
Line 39: Line 43:
'''Expression for <math> \Delta \vec{E}</math>
'''Expression for <math> \Delta \vec{E}</math>


Substitute the expression for the integration variable into the formula for the electric field of one slice. Separating the equation into separate x and y components, we get <math> \Delta \vec{E_x} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{-x}{(\sqrt{x^2+y^2})^{3/2}} \cdot dx  </math> and <math> \Delta \vec{E_y} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{y}{(\sqrt{x^2+y^2})^{3/2}} \cdot dx  </math>.  Note that we have replaced <math> \Delta x </math> with <math> dx</math> in preparation for integration.
Substitute the expression for the integration variable into the formula for the electric field of one slice. Separating the equation into separate x and y components, we get <math> \Delta \vec{E_x} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{-x}{(x^2+y^2)^{3/2}} \cdot dx  </math> and <math> \Delta \vec{E_y} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{y}{(x^2+y^2)^{3/2}} \cdot dx  </math>.  Note that we have replaced <math> \Delta x </math> with <math> dx</math> in preparation for integration.


'''Step 3: Add Up the Contributions of All the Pieces'''
'''Step 3: Add Up the Contributions of All the Pieces'''


The third step is to sum all of our slices.  We can go about this in two ways. One way is with numerical summation, or separating the object into a finite number of small pieces, calculating the individual contributing electric fields, and then summing them.  Another, more precise method is to integrate.  Most of the work of finding the field of a uniformly charged object is setting up this integral. If you have reached the correct expression to integrate, the rest is simple math.  The bounds for integration are the coordinates of the start and stop of the rod.  In this example the bounds are from <math>-L/2</math> to <math>+L/2</math>.  So the expression is <math> \int\limits_{-L/2}^{L/2}\ \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{y}{(\sqrt{x^2+y^2})^{3/2}} \cdot dx. </math>  Solving this gives the final expression <math> E_y = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{x} \cdot \frac{1}{(\sqrt{x^2+ (L/2)^2})}    </math>.  Note that the field parallel to the x axis is zero.  This can be observed due to the symmetry of the problem.  
The third step is to sum all of our slices.  We can go about this in two ways. One way is with numerical summation, or separating the object into a finite number of small pieces, calculating the individual contributing electric fields, and then summing them.  Another, more precise method is to integrate.  Most of the work of finding the field of a uniformly charged object is setting up this integral. If you have reached the correct expression to integrate, the rest is simple math.  The bounds for integration are the coordinates of the start and stop of the rod.  In this example the bounds are from <math>-L/2</math> to <math>+L/2</math>.  So the expression is <math> \int\limits_{-L/2}^{L/2}\ \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{y}{(x^2+y^2)^{3/2}} \cdot dx. </math>  Solving this gives the final expression <math> E_y = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{x} \cdot \frac{1}{(\sqrt{x^2+ (L/2)^2})}    </math>.  Note that the field parallel to the x axis is zero.  This can be observed due to the symmetry of the problem.  
This equation can be written more generally as <math> E = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r} \cdot \frac{1}{(\sqrt{r^2+ (L/2)^2})}    </math> where r represents the distance from the rod to the observation location.
This equation can be written more generally as <math> E = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r} \cdot \frac{1}{(\sqrt{r^2+ (L/2)^2})}    </math> where r represents the distance from the rod to the observation location.


Line 50: Line 54:
Finally, the fourth step is to check the result. The units should be the same as the units of the expression for the electric field for a single point particle <math> E = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r^2}    </math>.  
Finally, the fourth step is to check the result. The units should be the same as the units of the expression for the electric field for a single point particle <math> E = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r^2}    </math>.  
Our answer has the right units, since <math> \frac{1}{(\sqrt{x^2+ (L/2)^2})}    </math>. has the same units of <math>\frac{Q}{r^2}</math>
Our answer has the right units, since <math> \frac{1}{(\sqrt{x^2+ (L/2)^2})}    </math>. has the same units of <math>\frac{Q}{r^2}</math>
Is the direction qualitatively correct? We have the electric field pointing straight away from the midpoint of the rod, which is correct, given the symmetry of the situation. The vertical component of the electric field should indeed be zero.
Is the direction qualitatively correct? We have the electric field pointing straight away from the midpoint of the rod, which is correct, given the symmetry of the situation. The vertical component of the electric field should indeed be zero.


==== The System in Question ====
=== Computational Models ===
 
As discussed in the previous section, we're considering a system
abstracted from the particle model we're familiar with, therefore we will
make the generalization that our rod of length L has a total charge of
quantity Q. For this generalization, we will need to assume that the rod
is so thin that we can ignore its thickness.
 
[[Image:LukasYoder01.jpg|200px|center]]
 
Since the electric field produced by a charge at any given location is
proportional to the distance from the charge to that location, we will
need to relate the observation location to the source of the charge, which
we will consider the origin of the rod. To do that, we will need to divide
the rod into pieces of length <math>\Delta y</math> each containing a charge <math>\Delta Q</math>.
In the image below, you can see what this looks like and the relation that
can be found between the observation location and the source, forming the
distance vector <math>\vec{r}</math>.
 
[[Image:LukasYoder02.jpg|400px|center]]
 
By the pythagorean theorem, we can find the vector <math>\vec{r}</math> as follows:
 
[[Image:LukasYoder03.jpg|400px|center]]
 
 
And to find the unit vector in the direction of <math>\vec{r}</math>, <math>\hat{r}</math>, we do as
follows:
 
[[Image:LukasYoder04.jpg|400px|center]]
 


'''Finding the Electric Field from a Rod with Code'''
While computation done by hand does have its merits, and certainly was the
methodology used when these ideas were conceived, there are much more efficient,
powerful, and most importantly, pretty ways to go about finding and showing the
electric field. This is of course referring to computers, specifically computers
running glowscript code in the case of Physics 2212. With that idea in mind,
here are some demonstrations of said methodology:


==== Finding the Contribution of Each Piece to the Electric Field ====


Now that we've set up a model for the system, with the rod broken down
This is some code that you can run which shows the electric field vector
into pieces, we can find the contribution of each piece to the electric
field of the system. We will start from the electric field equation you
learned for a point particle but plug in the parameters for the rod system
into the equation.
 
[[Image:LukasYoder05.jpg|400px|center]]
 
 
By mathematically simplifying, we then get the following equation:
 
[[Image:LukasYoder06.jpg|400px|center]]
 
 
==== Finding the Net Contribution of all Pieces ====
 
In the previous section, we found out the contribution to the electric
field at a given location of only one of the pieces constituting the rod.
In order to figure out the net field at any particular location, we need
to add up the electric fields produced by individual pieces along the
length of the rod.
 
We will switch from vector notation for the electric field to the scalar
notation for the x- and y-components. (From the vector in the equation
above, we can see that the z-component of the electric field at any point
is always 0.) The x-component of the electric
field is the sum of the x-components of every <math>\Delta{y}</math> along the rod, and
the y-component of the electric field is the sum of the y-components of
every <math>\Delta{y}</math> along the rod. We can show this mathematically:
 
[[Image:LukasYoder07.jpg|400px|center]]
 
 
To make use of this relation, because we don't know <math>\Delta{Q}</math>, we need to
relate it to parameters that we already know about the rod system we're
analyzing. We can express <math>\Delta{Q}</math> as the charge density of the rod
(which is Q/L) times the <math>\Delta{y}</math> we've chosen for the system. Thus,
 
[[Image:LukasYoder08.jpg|200px|center]]
 
 
By plugging the above equation into our equations for the x- and
y-components of the electric field at a point, we can find the electric
field at any point in the system. This technique is called numerical
integration and is typically done by computers because the computational
complexity is dependant upon the size of <math>\Delta{y}</math> with respect to L.
 
==== Simplifying ====
 
Using calculus, we can simplify a lot of the math required to compute the
electric field at any given point. Notationally, all we're doing is switching from the
discretely-sized <math>\Delta{y}</math> to <math>dy</math> and from the sigma notation to
an integral starting from -L/2 (the lower end of the rod) and ending at
L/2 (the upper end of the rod) as follows:
 
[[Image:LukasYoder09.jpg|400px|center]]
[[Image:LukasYoder10.jpg|400px|center]]
 
 
By evaluating the integral, we can determine that the x-component of the
electric field at any point is:
 
[[Image:LukasYoder11.jpg|400px|center]]
 
 
Without evaluating the integral for the y-component of the electric field,
we can use symmetry to determine that the y-component of the electric
field at any given point is 0. Let's consider the contributions to the
electric field from the top and bottom halves of the rod at any
observation point.
 
[[Image:LukasYoder12.jpg|200px|center]]
 
 
Since the y-components of <math>E_{top}</math> and <math>E_{bottom}</math> are of equal magnitude and
opposite direction, they cancel each other out, and therefore the
y-component of teh electric field at any given point due to the rod is 0.
 
[[Image:LukasYoder13.jpg|200px|center]]
 
 
Finally, because the rod is round and can be rotated, as a convenience,
we'll use d (distance from the rod) as opposed to x (distance along the
x-direction) to refer to the electric field.
 
Thus we can simplify electric field calculations for a rod into a form
that we can readily use:
 
[[Image:LukasYoder14.jpg|400px|center]]
 
 
==== Further Simplification ====
 
By noting the contributions of each variable to the equation for the
electric field, we can make approximations to simplify our math by simply
declaring one variable as insignificant.
 
For example, if we have a system in which the length of a rod is much
greater than the magnitude of the distance from the rod (denoted L>>d), we
can neglect some of the instances in which d is taken into account as
follows:
 
[[Image:LukasYoder15.jpg|400px|center]]
 
=== A Computational Model ===
 
==== (Finding the Electric Field from a Rod with Code) ====
 
Here is some code that you can run which shows the electric field vector
at a given distance from the rod along its length. The rod is shown as a
at a given distance from the rod along its length. The rod is shown as a
series of green balls to help emphasize that when using the numerical
series of green balls to help emphasize that when using the numerical
integrations mentioned on this page, you are measuring the field produced
integrations mentioned on this page, you are measuring the field produced
by discrete parts of the rod being analyzed.
by discrete parts of the rod being analyzed. At each point of analysis,
eight field arrows are shown so as to visualize the electric field.


Notice the edge-effects of the electric field of the rod. For reasons
Notice the edge-effects of the electric field of the rod. For reasons
Line 205: Line 79:
effects would be negligible.
effects would be negligible.


[http://www.glowscript.org/#/user/yoderlukas/folder/Public/program/ElectricFieldAlongRodLength Click Here to Run the Code]
[http://www.glowscript.org/#/user/yoderlukas/folder/Public/program/ElectricFieldAlongRodLength '''Click Here to Run the Code''']
 
For a more precise model, the two links below lead to code that generates a
forty  element line of charge with given magnitude, and length, and then
iterates vectors representing the electric field in the space all around said
line of charge. Note that the vectors are small, but for the positively charged
rod, they lead radially outward, and for the negative, radially inward. This is
due to the fact that the rod(s) are treated as lines of positive or negative
charge, and the electric field behaves as such.
 
Try zooming in and out! You can really see the symmetry of the field far out,
and the edge effects when zoomed in.
 
[https://www.glowscript.org/#/user/michaelwise/folder/Public/program/LineofCharge-Positive '''Positive Charge''']
 
[https://www.glowscript.org/#/user/michaelwise/folder/Public/program/LineofCharge-Negative '''Negative Charge''']


==Examples==
==Examples==
Line 213: Line 102:
===Simple===
===Simple===


[[Image:LukasYoderNo.jpg|400px|center]]
[[Image:LukasYoderNo.jpg|800px|center|thumb|Figure1: Problem 1]]


===Middling===
===Middling===


[[Image:LukasYoderMaybe.jpg|400px|center]]
[[Image:LukasYoderMaybe.jpg|800px|center|thumb|Figure 2: Problem 2]]


===Difficult===
===Difficult===


[[Image:LukasYoderYes.jpg|400px|center]]
[[Image:LukasYoderYes.jpg|800px|center|thumb|Figure 3: Problem 3]]


== Connectedness ==
== Connectedness ==
The electrical field of a charged rod has many real world applications. Even within other areas of physics, you can extend what we know about a charged rod to find out the electric field of other objects. For instance, a ring is also just a rod that is bent in a circle. Further, a disk is a collection of many concentric rings. This method of thinking can lead us to some very interesting derivations for physics.


Electric fields are very important to electrical engineering because they can be used to convey signals. In fact, there is an entire sub-field of electrical engineering called digital signal processing that focuses on modulating different characteristics of radio frequency (RF) signals that are produced by electric fields.
Even if we are to only think about real life, rods exist everywhere. Since everything has an electrical field, any rod or even simply cylindrical shape or anything made of rods is an application. A very useful example that also comes up in physics is the concept of wires. Wires are, in essence, thin rods in which electrons can flow through. This categorizes them as a charged rod. Wires are not only an important subject in physics, but also real life as the device you are reading this on probably needed a wire for charge! What happens inside of the wire is important, but we also what happens outside of it is equally important. If we consider static electricity, a misunderstanding or a failure to account for static could be detrimental at a large scale as static can very easily cause malfunctioning to anything that uses wires to operate.  


I, the most recent editor of this page, see the use of the electric field of charged rods as a CS major constantly for a similar reason: wires. Computer Science and any form of software really only exists with accompanying hardware. Almost always, the connection between software and hardware is wires and the electrical pulses that serve as the data that travels along the wire. Especially as someone looking into robotics, it is important to understand the outward effect that wires have because static can be very tricky if you don't know how to handle it!
== History ==
== History ==


The history of the electric field can be found in a previous section on electric fields. The equation for the electric field of a charged rod was not a discovery, but simply a mathematical simplification that someone made to model a rod. As such, nobody knows who first made the mathematical simplification, where they made it, or when, though it was certainly made after electric fields were discovered.
Physicists and scientists make use of electric fields and charged objects all the time. Many times, we may need to know which objects are contributing how much charge in certain areas. Charged objects may attract or repel (depending on the signs of their charge), so we often need to know how objects will interact with each other based on their charges. The phenomenon of this interaction, or electric force between charged particles, was finally confirmed and stated as a law in 1785 by French physicist Charles-Augustin de Coulomb, hence "Coulomb's Law."


== See also ==
== See also ==


The equation for the electric field of a charged rod was derived from the equation for an electric field of a charged particle. See the article "[[Electric Field]]" for more information.
The equation for the electric field of a charged rod was derived from the equation for the electric field of a charged particle. See the article "[[Electric Field]]" for more information.


=== Further Reading ===
=== Further Reading ===
Line 240: Line 133:


=== External Links ===
=== External Links ===
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elelin.html


http://online.cctt.org/physicslab/content/phyapc/lessonnotes/Efields/EchargedRods.asp
http://online.cctt.org/physicslab/content/phyapc/lessonnotes/Efields/EchargedRods.asp
Line 248: Line 142:


== References ==
== References ==
https://www.glowscript.org/#/
https://rhettallain_gmail_com.trinket.io/intro-to-electric-and-magnetic-fields#/electric-fields/multiple-charges


https://www.youtube.com/watch?v=BBWd0zUe0mI
https://www.youtube.com/watch?v=BBWd0zUe0mI


(For the above reference, I chose to follow the textbook's method in not defining the charge distribution and assuming it was constant, though this was helpful in figuring out a better way to introduce it.)
(For the above reference, the textbook's method is followed in that the charge distribution was left undefined, and assumed to be constant)


Chabay and Sherwood: Matter and Interactions, Fourth Edition, Chapter 15
Chabay and Sherwood: Matter and Interactions, Fourth Edition, Chapter 15


All figures created by author
 
[[Category: Electric Field]]
[[Category: Electric Field]]

Latest revision as of 03:11, 15 April 2024

Sajan Thomas, Spring 2024

The Main Idea

Previously, we've learned about the electric field of a point particle. While this skill does build the fundamentals of E&M physics, the real world is not simply made up of isolated particles. In fact, the world is consisted of many geometric shapes our one equation for the electric field of a particle cannot account for. One such example of these geometric shapes is a rod.

For the purposes of this course's scope, we assume that the charge is uniformly distributed along the rod. This is an important assumption to make since if it weren't the case, a lot of the calculations would change. This in mind, let's start with what we know: the electric field of a point particle. By itself, we can't represent a rod. But, if we stack a lot of charged particles together closely in a line, what do we get? a rod. That is the basis of how we calculate the electric field of a charged rod.

That's the basis of it but for now, we'll keep that for later when we're actually deriving how to find it. First, let's discuss the factors that can contribute to the electric field of the charged rod. Firstly, as with any electric field, we have to know the charge of the source-- in this case, the rod. Secondly, we have to know the length of the rod. Thirdly, we also should know the observation location to find the radius from the rod.

The process of finding the electric field due to charge distributed over an object has four steps:

1. Consider the rod, as previously discussed, as a collection of many, many, infinitesimally small charged particles. Make a diagram and draw the electric field [math]\displaystyle{ \Delta \vec{E} }[/math] contributed by one of the pieces.

2. By drawing the vectors for the [math]\displaystyle{ \Delta \vec{E} }[/math] contributed to one piece, and repeating it along the rod, you should realize by symmetry that several of the vector components will cancel out.

3. Add up the contributions of all pieces, either numerically or symbolically. While there is a formula we can just apply simply later, this step requires integration as you are adding all of the [math]\displaystyle{ \Delta \vec{E} }[/math] contributions of many, many, charged particles.

4. Check that the result is physically correct.

A Mathematical Model

The process of calculating a uniformly charged rod's electric field is tedious, but breaking the process down into several steps makes the task at hand easier. Consider a uniformly charged thin rod of length [math]\displaystyle{ L }[/math] and positive charge [math]\displaystyle{ Q }[/math] centered on and lying along the x-axis. The rod is being observed from above at a point on the y-axis.

Figure 2: Problem 2

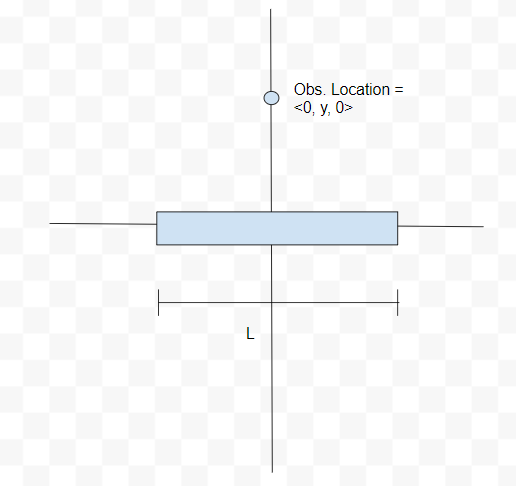
Step 1: Divide the Distribution into Pieces; Draw [math]\displaystyle{ \Delta \vec{E} }[/math]

Imagine dividing the rod into a series of very thin slices, each with the same charge [math]\displaystyle{ \Delta Q }[/math]. This charge [math]\displaystyle{ \Delta Q }[/math] is a small part of the overall charge. Picture it as a point charge. Each slice contributes its own electric field, [math]\displaystyle{ \Delta E }[/math]. Summing all these individual slices of [math]\displaystyle{ E }[/math] gives you the total electric field of the rod. This process approaches taking an integral, as each thickness approaches 0 and the the number of slices approaches infinity. Note that in this example, the variable that is changing for each slice is its x-coordinate.

Figure 2: Problem 2


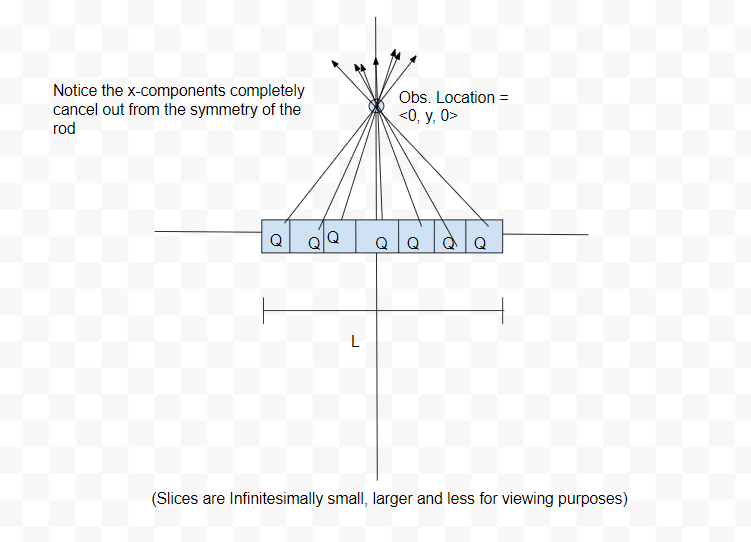
Step 2: Write an Expression for the Electric Field Due to One Piece

The second step is to write a mathematical expression for the field [math]\displaystyle{ \Delta E }[/math] contributed by a single slice of the rod. We use the formula of the electric field for a point charge because we are imagining each slice as a point charge. First, determine [math]\displaystyle{ r }[/math], the vector pointing from the source to the observation location. For our example, this is [math]\displaystyle{ r = obs - source = \lt 0,y,0\gt - \lt x,0,0\gt = \lt -x,y,0\gt }[/math]. Now use this to calculate the magnitude and direction of [math]\displaystyle{ r }[/math]. So [math]\displaystyle{ |\vec{r}| = \sqrt{(-x)^2 + y^2} = \sqrt{x^2 + y^2} }[/math] and [math]\displaystyle{ \hat{r} = \frac{\vec{r}}{\hat{r}} = \frac{\lt -x,y,0\gt }{\sqrt{x^2 + y^2}} }[/math]. [math]\displaystyle{ \hat{r} }[/math] is the vector portion of the expression for the field. The scalar portion is [math]\displaystyle{ \frac{1}{4\pi\epsilon_0} \cdot \frac{\Delta Q}{|\vec{r}|^2} }[/math]. Thus the expression for one slice of the rod is: [math]\displaystyle{ \Delta \vec{E} = \frac{1}{4\pi\epsilon_0} \cdot \frac{\Delta Q}{(x^2+y^2)^{3/2}} \cdot \lt -x,y,0\gt }[/math].

Determining [math]\displaystyle{ \Delta Q }[/math] and the integration variable

In the first step, we determined that the changing variable for this rod was its x-coordinate. This means the integration variable is [math]\displaystyle{ dx }[/math]. We need to put this integration variable into our expression for the electric field. More specifically, we need to express [math]\displaystyle{ \Delta Q }[/math] in terms of the integration variable. Recall that the rod is uniformly charged, so the charge on any single slice of it is: [math]\displaystyle{ \Delta Q = (\frac{\Delta x}{L})\cdot Q }[/math]. This quantity can also be expressed in terms of the charge density.

Expression for [math]\displaystyle{ \Delta \vec{E} }[/math]

Substitute the expression for the integration variable into the formula for the electric field of one slice. Separating the equation into separate x and y components, we get [math]\displaystyle{ \Delta \vec{E_x} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{-x}{(x^2+y^2)^{3/2}} \cdot dx }[/math] and [math]\displaystyle{ \Delta \vec{E_y} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{y}{(x^2+y^2)^{3/2}} \cdot dx }[/math]. Note that we have replaced [math]\displaystyle{ \Delta x }[/math] with [math]\displaystyle{ dx }[/math] in preparation for integration.

Step 3: Add Up the Contributions of All the Pieces

The third step is to sum all of our slices. We can go about this in two ways. One way is with numerical summation, or separating the object into a finite number of small pieces, calculating the individual contributing electric fields, and then summing them. Another, more precise method is to integrate. Most of the work of finding the field of a uniformly charged object is setting up this integral. If you have reached the correct expression to integrate, the rest is simple math. The bounds for integration are the coordinates of the start and stop of the rod. In this example the bounds are from [math]\displaystyle{ -L/2 }[/math] to [math]\displaystyle{ +L/2 }[/math]. So the expression is [math]\displaystyle{ \int\limits_{-L/2}^{L/2}\ \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{L} \cdot \frac{y}{(x^2+y^2)^{3/2}} \cdot dx. }[/math] Solving this gives the final expression [math]\displaystyle{ E_y = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{x} \cdot \frac{1}{(\sqrt{x^2+ (L/2)^2})} }[/math]. Note that the field parallel to the x axis is zero. This can be observed due to the symmetry of the problem. This equation can be written more generally as [math]\displaystyle{ E = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r} \cdot \frac{1}{(\sqrt{r^2+ (L/2)^2})} }[/math] where r represents the distance from the rod to the observation location.

Step 4:Checking the Result

Finally, the fourth step is to check the result. The units should be the same as the units of the expression for the electric field for a single point particle [math]\displaystyle{ E = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r^2} }[/math]. Our answer has the right units, since [math]\displaystyle{ \frac{1}{(\sqrt{x^2+ (L/2)^2})} }[/math]. has the same units of [math]\displaystyle{ \frac{Q}{r^2} }[/math]

Is the direction qualitatively correct? We have the electric field pointing straight away from the midpoint of the rod, which is correct, given the symmetry of the situation. The vertical component of the electric field should indeed be zero.

Computational Models

Finding the Electric Field from a Rod with Code While computation done by hand does have its merits, and certainly was the methodology used when these ideas were conceived, there are much more efficient, powerful, and most importantly, pretty ways to go about finding and showing the electric field. This is of course referring to computers, specifically computers running glowscript code in the case of Physics 2212. With that idea in mind, here are some demonstrations of said methodology:


This is some code that you can run which shows the electric field vector at a given distance from the rod along its length. The rod is shown as a series of green balls to help emphasize that when using the numerical integrations mentioned on this page, you are measuring the field produced by discrete parts of the rod being analyzed. At each point of analysis, eight field arrows are shown so as to visualize the electric field.

Notice the edge-effects of the electric field of the rod. For reasons discussed above, if we used the long rod approximation (L>>d), these effects would be negligible.

Click Here to Run the Code

For a more precise model, the two links below lead to code that generates a forty element line of charge with given magnitude, and length, and then iterates vectors representing the electric field in the space all around said line of charge. Note that the vectors are small, but for the positively charged rod, they lead radially outward, and for the negative, radially inward. This is due to the fact that the rod(s) are treated as lines of positive or negative charge, and the electric field behaves as such.

Try zooming in and out! You can really see the symmetry of the field far out, and the edge effects when zoomed in.

Positive Charge

Negative Charge

Examples

Although this is not a very difficult topic, some reasonably difficult conceptual questions can be asked about it.

Simple

Figure1: Problem 1

Middling

Figure 2: Problem 2

Difficult

Figure 3: Problem 3

Connectedness

The electrical field of a charged rod has many real world applications. Even within other areas of physics, you can extend what we know about a charged rod to find out the electric field of other objects. For instance, a ring is also just a rod that is bent in a circle. Further, a disk is a collection of many concentric rings. This method of thinking can lead us to some very interesting derivations for physics.

Even if we are to only think about real life, rods exist everywhere. Since everything has an electrical field, any rod or even simply cylindrical shape or anything made of rods is an application. A very useful example that also comes up in physics is the concept of wires. Wires are, in essence, thin rods in which electrons can flow through. This categorizes them as a charged rod. Wires are not only an important subject in physics, but also real life as the device you are reading this on probably needed a wire for charge! What happens inside of the wire is important, but we also what happens outside of it is equally important. If we consider static electricity, a misunderstanding or a failure to account for static could be detrimental at a large scale as static can very easily cause malfunctioning to anything that uses wires to operate.

I, the most recent editor of this page, see the use of the electric field of charged rods as a CS major constantly for a similar reason: wires. Computer Science and any form of software really only exists with accompanying hardware. Almost always, the connection between software and hardware is wires and the electrical pulses that serve as the data that travels along the wire. Especially as someone looking into robotics, it is important to understand the outward effect that wires have because static can be very tricky if you don't know how to handle it!


History

Physicists and scientists make use of electric fields and charged objects all the time. Many times, we may need to know which objects are contributing how much charge in certain areas. Charged objects may attract or repel (depending on the signs of their charge), so we often need to know how objects will interact with each other based on their charges. The phenomenon of this interaction, or electric force between charged particles, was finally confirmed and stated as a law in 1785 by French physicist Charles-Augustin de Coulomb, hence "Coulomb's Law."

See also

The equation for the electric field of a charged rod was derived from the equation for the electric field of a charged particle. See the article "Electric Field" for more information.

Further Reading

The page on electric fields: Electric Field

External Links

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elelin.html

http://online.cctt.org/physicslab/content/phyapc/lessonnotes/Efields/EchargedRods.asp

https://pages.uncc.edu/phys2102/online-lectures/chapter-02-electric-field/2-4-electric-field-of-charge-distributions/example-1-electric-field-of-a-charged-rod-along-its-axis/

http://dev.physicslab.org/Document.aspx?doctype=3&filename=Electrostatics_ContinuousChargedRod.xml

References

https://www.glowscript.org/#/

https://rhettallain_gmail_com.trinket.io/intro-to-electric-and-magnetic-fields#/electric-fields/multiple-charges

https://www.youtube.com/watch?v=BBWd0zUe0mI

(For the above reference, the textbook's method is followed in that the charge distribution was left undefined, and assumed to be constant)

Chabay and Sherwood: Matter and Interactions, Fourth Edition, Chapter 15

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Field_of_a_Charged_Rod&oldid=46306"