Current in an RL Circuit

Claimed by Josh Mathew Fall 2016

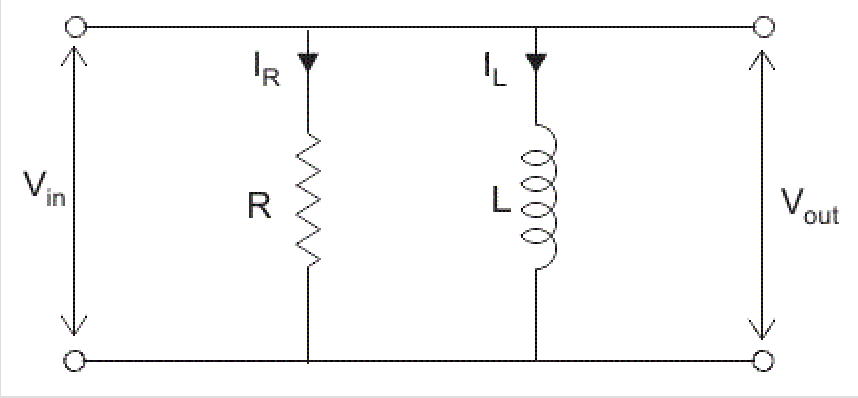
This topic describes the current in a RL circuit. An RL circuit includes a resistor (R) and inductor (L). Thus it is apart of the Inductor circuits along with the LC circuit. This is powered through a voltage or current. A common use of the RL circuit is to DC power supplies to RF amplifiers which is pictured below.

The Main Idea

In order to figure out the current of a RL circuit we must figure out exactly what a RL circuit entails and what the different uses of it are.

RL circuits essentially just include a resistor and inductor. An inductor is a mechanism that essentially able to store energy in a magnetic field. Inductors are useful because they can help reduce resistance especially in A.C. However in a DC, an inductor is a stable resistor. An important point about the energy of an Inductor is that it is kept in magnetic fields. Which is caused by the current and inductance. A resistor is device that regulates the current in a circuit. They can also be used to create a specific voltage. The RL circuit can be used in either parallel or series and they can be used as a low or high passive filters. The difference between the two is that a low passive filter lets frequencies below the threshold to pass. A high pass filter allows frequencies greater than the threshold to pass.

Two types of RL currents we must take into account are those with batteries and those without batteries. The first type includes a inductor, resistor with a battery. When the switch is closed, the inductors contributes resistance to the circuit, and current will reach the same value with the resistor, however it will have to add up at a exponential rate. However if the system was only the resistor and battery, we would only have a current when the switch is closed. In a circuit without a battery, after the current is at a steady state the resistor would cause the current to immediately drop to zero after the switch is turned off. However with the use of an inductor will oppose the sudden drop to the current. So after some time it will reach zero but with a significant amount of time. It is important to note that the inductor does cause a slight "sluggishness" in the circuit.

Included in a RL circuit is Impedance, which is the "effective" resistance within an electrical circuit. This impedance is frequency dependent as well.

In order to figure out the current in a RL circuit we must first have a series of proofs that includes the resistance, inductance, and emf of the battery. Essentially to being figuring out the current of the RL circuit we must first have to find the energy conservation loop for the series circuit. After substituting equivalent terms we are able to proof what the current of a RL circuit would be with a large enough T

A Mathematical Model

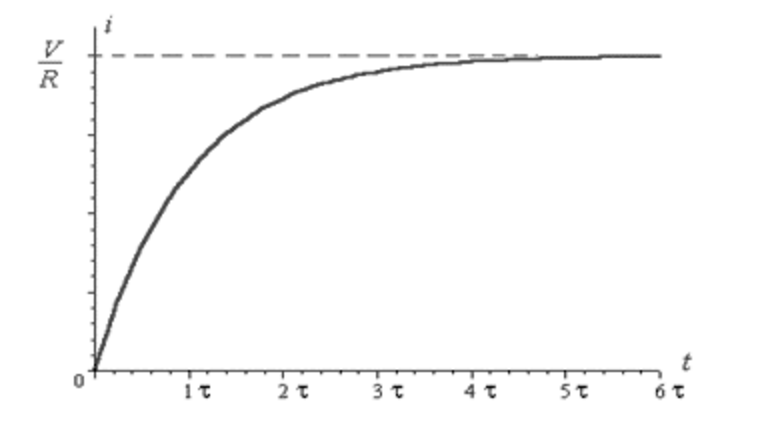
This image is a graph of current vs. time in the RL circuit. It starts at zero because the switch was closed at t= 0.

The energy conservation loop rule for the series circuit is below.

ΔV(battery) + ΔV(resistor) + ΔV(inductor) = 0

Things we must substitute

ΔV(battery) = emf(battery)

ΔV(resistor) = RI

ΔV(inductor) = L(dI/dt)

What we get

emf(battery) - RI - L(dI/dt) = 0

- It is important to note that the L(dI/dt) is negative because inductance acts in the opposite of the increasing current

From here you can solve for the current, and get

After separating variables and and taking the integral with the appropriate limits [0 - t] and [0-I]

We must also power both sides of the equation to e

We would get.

I = (emf(battery)/R) * [ 1-e^(-(R/L)t ]

In order to prove this we must substitute I and dI/dt in the first equation that we had found. After careful inspection we can tell that after a very large value for t , e^(-(R/L)t approaches a very small number which is essentially zero.

Therefore the only terms left are I = (emf(battery)/R) : This depicts steady-state current.

In order to measure the time for it to reach this steady state we must implement the "time constant" which is (L/R)

t = L/R

e^((-R/L)(L/R)) = 1/e = .37

The current would reach the maximum value at a faster rate without the inductor. . This value proves the "lag" that an inductor has on the current of a circuit.

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

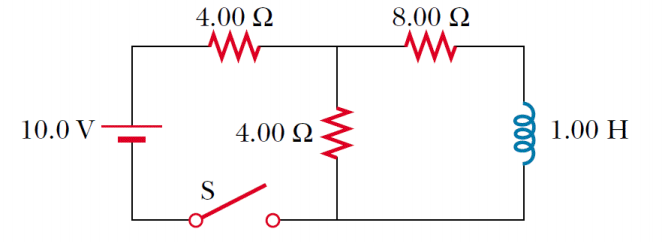
For the RL circuit in the figure, R1 = 4Ω (leftmost one in the figure), R2 = 4Ω ( middle in the figure), and R3 = 8Ω. The currents in R1, R2, and R3 are denoted as I1, I2, and I3, respectively. The voltage drops across R1, R2, R3 and the inductance L are denoted as V1, V2, V3, and VL, respectively. Suppose that initially there is no current in the inductor, and the switch is open.

Simple

Close the switch, and find I3 immediately after the switch is closed

Solution

As proved by Lenz's rule since the inductor is in the opposite direction from the change in current thus I3 = 0

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

Matter & Interactions 4th Edition: Electric and Magnetic Interactions