Current in an RL Circuit

Claimed by Josh Mathew Fall 2016

This topic describes the current in a RL circuit. An RL circuit includes a resistor (R) and inductor (L). Thus it is apart of the Inductor circuits along with the LC circuit. This is powered through a voltage or current. A common use of the RL circuit is to DC power supplies to RF amplifiers which is pictured below.

The Main Idea

In order to figure out the current of a RL circuit we must figure out exactly what a RL circuit entails and what the different uses of it are.

RL circuits essentially just include a resistor and inductor. An inductor is a mechanism that essentially able to store energy in a magnetic field. Inductors are useful because they can help reduce resistance especially in A.C. However in a DC, an inductor is a stable resistor. An important point about the energy of an Inductor is that it is kept in magnetic fields. Which is caused by the current and inductance. A resistor is device that regulates the current in a circuit. They can also be used to create a specific voltage. The RL circuit can be used in either parallel or series and they can be used as a low or high passive filters. The difference between the two is that a low passive filter lets frequencies below the threshold to pass. A high pass filter allows frequencies greater than the threshold to pass.

Two types of RL currents we must take into account are those with batteries and those without batteries. The first type includes a inductor, resistor with a battery. When the switch is closed, the inductors contributes resistance to the circuit, and current will reach the same value with the resistor, however it will have to add up at a exponential rate. However if the system was only the resistor and battery, we would only have a current when the switch is closed. In a circuit without a battery, after the current is at a steady state the resistor would cause the current to immediately drop to zero after the switch is turned off. However with the use of an inductor will oppose the sudden drop to the current. So after some time it will reach zero but with a significant amount of time. It is important to note that the inductor does cause a slight "sluggishness" in the circuit.

Included in a RL circuit is Impedance, which is the "effective" resistance within an electrical circuit. This impedance is frequency dependent as well.

In order to figure out the current in a RL circuit we must first have a series of proofs that includes the resistance, inductance, and emf of the battery. Essentially to being figuring out the current of the RL circuit we must first have to find the energy conservation loop for the series circuit. After substituting equivalent terms we are able to proof what the current of a RL circuit would be with a large enough T

A Mathematical Model

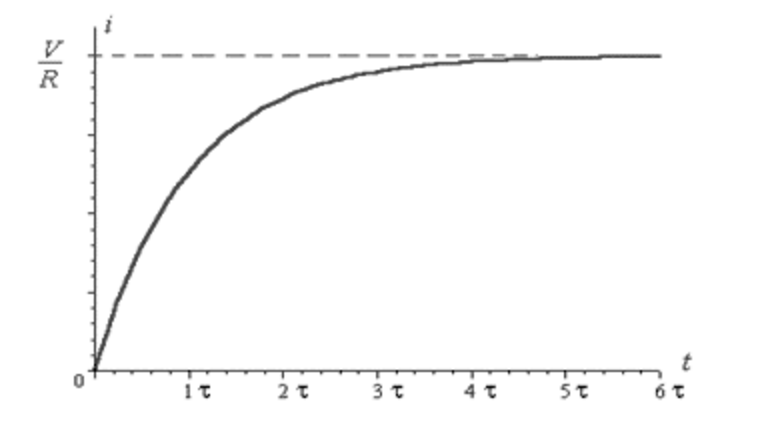
This image is a graph of current vs. time in the RL circuit. It starts at zero because the switch was closed at t= 0.

The energy conservation loop rule for the series circuit is below.

ΔV(battery) + ΔV(resistor) + ΔV(inductor) = 0

Things we must substitute

ΔV(battery) = emf(battery)

ΔV(resistor) = RI

ΔV(inductor) = L(dI/dt)

What we get

emf(battery) - RI - L(dI/dt) = 0

- It is important to note that the L(dI/dt) is negative because inductance acts in the opposite of the increasing current

From here you can solve for the current, and get

After separating variables and and taking the integral with the appropriate limits [0 - t] and [0-I]

We must also power both sides of the equation to e

We would get.

I = (emf(battery)/R) * [ 1-e^(-(R/L)t ]

In order to prove this we must substitute I and dI/dt in the first equation that we had found. After careful inspection we can tell that after a very large value for t , e^(-(R/L)t approaches a very small number which is essentially zero.

Therefore the only terms left are I = (emf(battery)/R) : This depicts steady-state current.

In order to measure the time for it to reach this steady state we must implement the "time constant" which is (L/R)

t = L/R

e^((-R/L)(L/R)) = 1/e = .37

The current would reach the maximum value at a faster rate without the inductor. . This value proves the "lag" that an inductor has on the current of a circuit.

A Computational Model

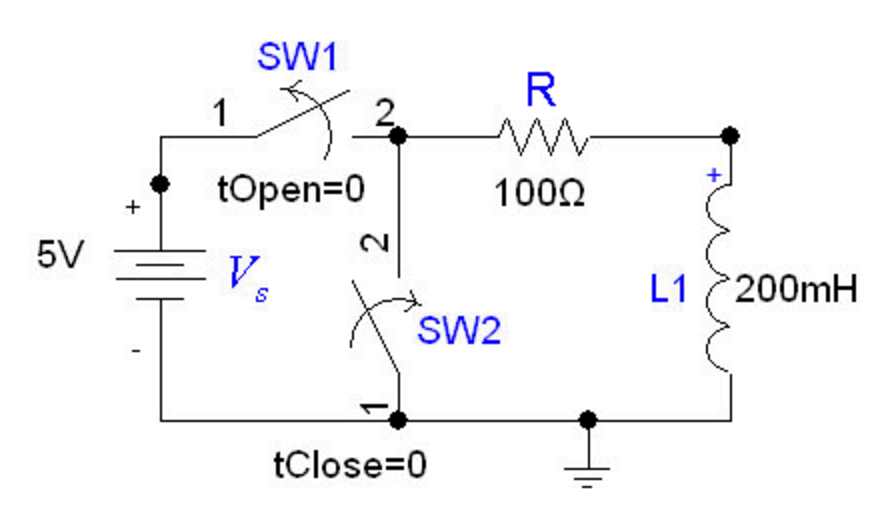
The following is a picture of a RL circuit discharging

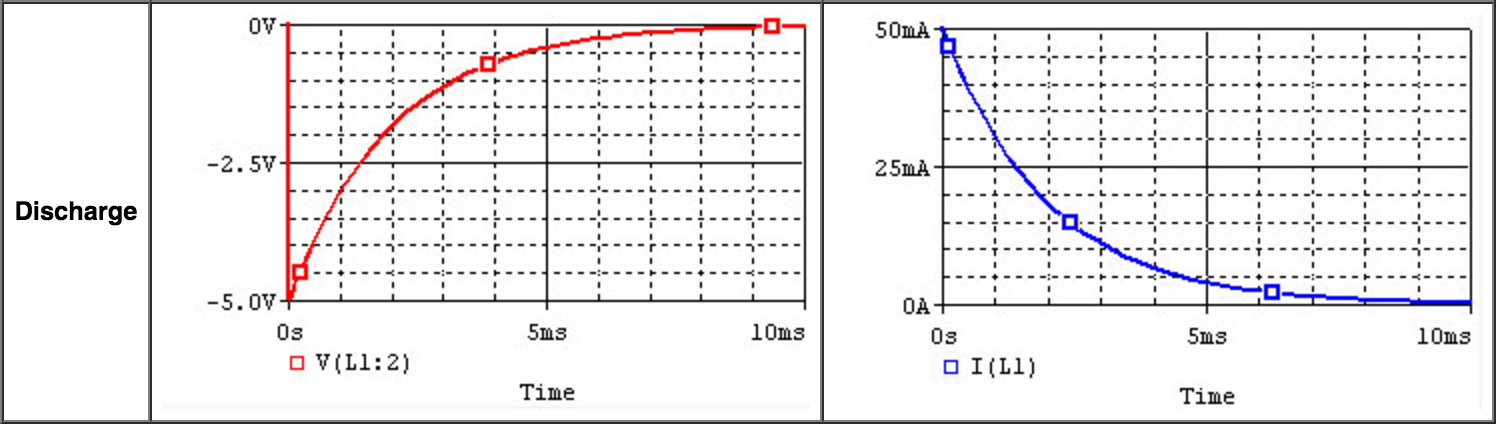
The following calculated graph measures the discharging voltage and current. The red graph is voltage and the blue graph is current.

Examples

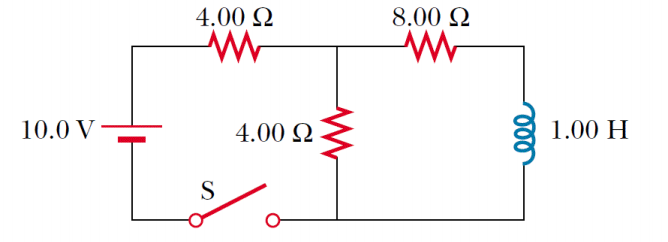
For the RL circuit depicted, R1 = 4Ω , R2 = 4Ω , and R3 = 8Ω. The currents in R1, R2, and R3 are I1, I2, and I3, respectively. The voltage drops across R1, R2, R3 and the inductance L are denoted as V1, V2, V3, and VL, respectively. At first the switch is open and there is no current in the inductor.

Simple

Close the switch, and find I3 immediately after the switch is closed

Solution

As proved by Lenz's rule since the inductor is in the opposite direction from the change in current, I3 = 0.

Middling

Find Kirchoff’s loop rule, and find I1 and I2.

Solution

ε − I1R1 − I2R2 = 0

We can assume I1=I2

From the diagram we can see that ε = 10v, R1= 4Ω, R2 = 4Ω

Therefore we get

10 − 8I1 = 0.

I1 = I2 = 10/8 (A)

Difficult

After the switch is closed for a very long time, find I1.

Solution

The key word here is, closed, since it is closed for a very long time the current reaches steady state. Thus VL = L∆I3/∆t = 0

This tells us that R2 and R3 and in parallel. This also tells us that they are in series with R1.

Req = R1 + ((R2R3)/ (R2 + R3)) = (4 + 4 × 8)/(4 + 8) = 20/3(Ω).

In order to get I1 we set it equal to I(eq) which is equivalent to 10/ R(eq) = 10/(20/3) = 1.5(A)

Connectedness

How is this topic connected to something that you are interested in?

Growing up I was always curious about how certain circuits are better for certain applications than others. And I never fully understood how Inductors played a role in circuits and how they can affect the current of a circuit. So this helped me understand those certain topics.

How is it connected to your major?

I assume this will be very useful for a major like electrical engineering. However, while it may not be directly connected to my major ,Industrial Engineering, there is a indirect connection. It was noted that the popularity and use of RL is not as high as certain other circuits. So from a production and manufacturing stand point, I may have to figure out a more efficient way to produce these products without affecting the production potential of other circuits.

Is there an interesting industrial application?

RL circuits can be used for DC power supplies for RF amplifiers, this is where the inductor is utilized to proceed DC bias current and it will not allow the RF to go back to the power supply.

History

There is not much discovery of the RL circuit alone, that may be partially due to the fact that the discovery of the RLC circuit also uncovered many concepts that affected the RL circuit. The first time an individual could tell that a capacitor could make electrical oscillation was by Felix Savary in 1826. Then from there multiple advancements occurred by different scientists, such as the German Physicist Heinrich Hertz who noted recorded a electrical resonance curve. Then from there demonstrations of resonance between tuned circuits occurred with Lodges, syntonic jars experiment in 1889. After research and multiple papers being published, RLC circuits were used for radio transmitters in the 1890's. The first usable radio was actually invented in 1900 by Italian Guglielmo Marconi. Therefore around this time frame or possibly later the practical use for just a RL circuit was also made.

http://physics.info/circuits-rl/

http://physics.bu.edu/~duffy/semester2/c19_RL.html

http://hades.mech.northwestern.edu/index.php/RC_and_RL_Exponential_Responses

https://en.wikipedia.org/wiki/RLC_circuit#History

Current in an RL Circuit

Contents

The Main Idea

A Mathematical Model

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu