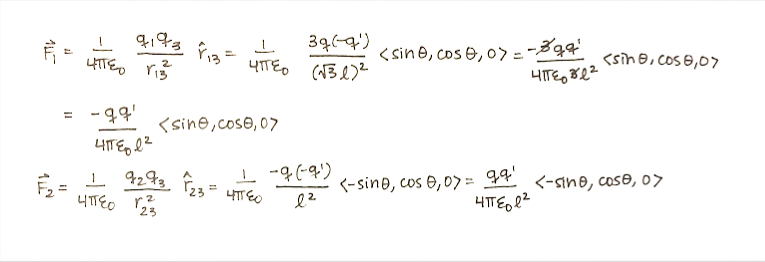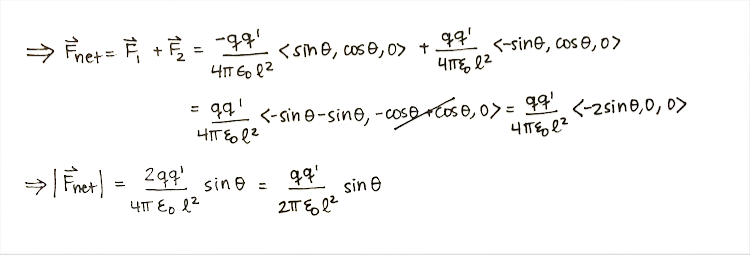Electric Force
CLAIMED BY Luis Pimentel Spring 2018
The Main Idea
There are two kinds of electric charge: positive and negative. Particles with like charges will repel each other, and particles with unlike charges attract each other. Calling a particle a "point particle" signifies an object with a radius so small in comparison to the distance between it and all other objects of interest. The object is then treated as if all its charge and mass were concentrated at a single point. Many times protons and electrons can be considered point particles due to its size.
The Electric Field created by a charge contains a force that is exerted on other charged particles or objects called an electric force. The strength of this electrical interaction is a vector quantity that has magnitude and direction. If the electric field at a particular location is known, then this field can be used to calculate the electric force of the particle being acted upon. The electric force is directly proportional to the amount of charge within each particle being acted upon by the other's electric field. Moreover, the magnitude of the force is inversely proportional to the square distance between the two interacting particles. It is important to remember that a particle cannot have an electric force on itself; there must be at least two interacting, charged components.
A Mathematical Model
The Coulomb Force Law The formula for the magnitude of the electric force between two point charges is:
[math]\displaystyle{ F=\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}{q}_{2}|}{r^2} }[/math], where [math]\displaystyle{ {q}_{1} }[/math] and [math]\displaystyle{ {q}_{2} }[/math] are the magnitudes of electric charge of point 1 and point 2, and [math]\displaystyle{ r }[/math] is the distance between the two point charges. The units for electric force are in Newtons. The expression [math]\displaystyle{ \frac{1}{4 \pi \epsilon_0 } }[/math] is known as the electric constant and carries the value 9e9. Epsilon 0 defines electric permittivity of space.
Interestingly enough, one can see a relationship between this formula and the formula for gravitational force ([math]\displaystyle{ F={G} \frac{|{m}_{1}{m}_{2}|}{r^2} }[/math]). From this relationship, one can conclude that the interactions of two objects as a result of their charges or masses follow similar fundamental laws of physics.
Derivations of Electric Force
The electric force on a particle can also be written as:
[math]\displaystyle{ \vec F=q\vec E }[/math], where [math]\displaystyle{ q }[/math] is the charge of the particle and [math]\displaystyle{ \vec E }[/math] is the external electric field.
This formula can be derived from [math]\displaystyle{ |\vec F|=\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}{q}_{2}|}{r^2} }[/math], the electric force between two point charges. The magnitude of the electric field created by a point charge is [math]\displaystyle{ |\vec E|=\frac{1}{4 \pi \epsilon_0 } \frac{|q|}{r^2} }[/math], where [math]\displaystyle{ q }[/math] is the magnitude of the charge of the particle and [math]\displaystyle{ r }[/math] is the distance between the observation location and the point charge. Therefore, the magnitude of electric force between point charge 1 and point charge 2 can be written as:
[math]\displaystyle{ |\vec F|=\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}{q}_{2}|}{r^2}=|{q}_{2}|\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}|}{r^2}=|{q}_{2}||\vec{E}_{1}| }[/math]
The units of charge are in Coulombs and the units for electric field are in Newton/Coulombs, so this derivation is correct in its dimensions since multiplying the two units gives just Newtons. The Newton is the unit for electric force.
A Computational Model
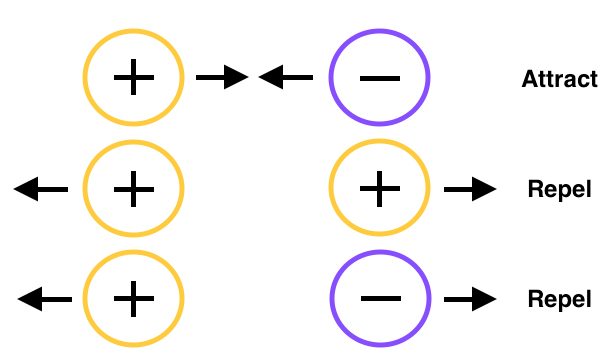
Direction of the Electric Force
The electric force is along a straight line between the two point charges in the observed system. If the point charges have the same sign (i.e. both are either positively or negatively charged), then the charges repel each other. If the signs of the point charges are different (i.e. one is positively charged and one is negatively charged), then the point charges are attracted to each other. The electric force vector acts either in the same or opposite direction of the electric field acting on a particle, depending on the charge of that particle. Remember that negative charges attract, so the electric field of a negative charge will act from the observation location towards the charged negatively charged particle. If the observation particle is positively charged, then the electric force will act in the same direction as the electric field. If the observation particle is negatively charged, then the force will act in the opposite direction as the electric field. The same concepts apply to positive electric fields, which point away from the source location at the observation location.
Electric force follows Newton's third law of equal and opposite forces, meaning that the electric force experienced by one of the two interacting objects will be equal and opposite to the electric force of the first object.
A computational representation of the Electric force can be created using VPython. The code below shows how we can find the net force, momentum and final position between two charged particles in VPython. This example uses two positively charged protons.
#CONSTANTS
E= 9e9 # Electric Force constant
q1 = +1.6e-19 # Charge of proton 1
q2 = +1.6e-19 # Charge of proton 2
while t < 200 :
# Calculate electric force acting on proton 1 by proton 2
r = proton.pos - proton2.pos
rmag = mag(r)
rhat = r/rmag
Fnet = E*((q1*q2)/(mag2(r)))*rhat
# Calculate electric force acting on proton 1 by proton 2
r2 = proton2.pos - proton.pos
rmag2 = mag(r2)
rhat2 = r2/rmag2
Fnet2 = E*((q1*q2)/(mag2(r2)))*rhat2
# Update positions of BOTH protons
pproton = pproton + Fnet*deltat
vproton = pproton/mproton
proton.pos = proton.pos + vproton*deltat
pproton2 = pproton2 + Fnet2*deltat
vproton2 = pproton2/mproton
proton2.pos = proton2.pos + vproton2*deltat
Notice that this iterative process is very similar to that working with Gravitational Forces.
Notice, however, that the direction of motion of each particle is not determined by relative position, but by the charges of the particles. The product of these charges ultimately determine whether the two particles will attract each other, or repel. This is demonstrated in the following simulations:
The trinket model linked demonstrates the Electric force interaction of a proton and an electron. Proton-Electron Electric Force Interaction
The trinket model linked demonstrates the Electric force interaction between two protons. Proton-Proton Electric Force Interaction
Examples
Simple
Problem: Find the electric force of a -3 C particle in a region with an electric field of [math]\displaystyle{ \lt 7, 5, 0\gt }[/math]N/C.
Step 1: Substitute values into the correct formula.
[math]\displaystyle{ \vec F=q\vec E }[/math]
[math]\displaystyle{ \vec F=(-3 C)\lt 7, 5, 0\gt }[/math]N/C
[math]\displaystyle{ \vec F=\lt -21, -15, 0\gt }[/math]N
The electric force vector for this particle is [math]\displaystyle{ \lt -21, -15, 0\gt }[/math]N.
Midding
Problem: Find the magnitude of electric force on two charged particles located at [math]\displaystyle{ \lt 0, 0, 0\gt }[/math]m and [math]\displaystyle{ \lt 0, 10, 0\gt }[/math]m. The first particle has a charge of +5 nC and the second particle has a charge of -10 nC. Is the force attractive or repulsive?
Step 1: Find the distance between the two point charges.
[math]\displaystyle{ d=\sqrt{(0 m-0 m)^2+(0 m-10 m)^2+(0 m-0 m)^2}=\sqrt{100 m}=10 }[/math]m.
The distance between the two points is 10 m.
Step 2: Substitute values into the correct formula.
[math]\displaystyle{ |\vec F|=\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}{q}_{2}|}{r^2}=\frac{1}{4 \pi \epsilon_0 } \frac{|(5 nC)(-10 nC)|}{(10m)^2} }[/math]
[math]\displaystyle{ |\vec F|=4.5e-9 }[/math] N
The magnitude of electric force is [math]\displaystyle{ |\vec F|=4.5e-9 }[/math] N.
Step 3: Determine if force is attractive or repulsive.
Since the first particle is positively charged and the second is negatively charged, the force is attractive. The particles are attracted to each other.
Difficult
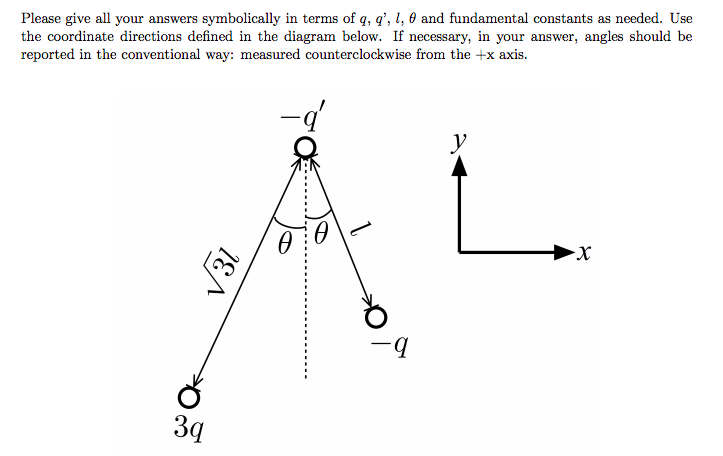
Problem:
Using the graphic above, find a) the net force acting on particle -q' and b) the direction of the net force on this charge.
Step 1: Calculate the net force.
Step 2: Evaluate the direction of the force.
Problems involving electric force exclusively will not be more complicated than the above. However, the the electric force can be used in calculation of a net force acting on a particle in combination with non-Coulomb electric force and magnetic force.
Connectedness
Electric force is ubiquitous in everyday life, although it is not always evident. One common example of electric force is the attraction of clothes to one another after being washed. The charges caused by the machine-drying process create opposite, attractive charges on different pieces of clothing which cause them to stick together. Another example can be seen in refrigerator magnets due to the electromagnetic forces that enable magnetism. Thinking more complexly, the electric force is also prevalent in almost all forms of modern technology involving electricity. One particular example is the process of charging a smartphone: the electric force allows a current to be generated which transfers charge from outlets to the internal battery of these devices. A final, slightly more complicated example of the electric force is seen in the production of abrasive paper, whereby positively charged-smoothing particles are attracted to a negatively charged, smooth surface to create papers like sandpaper.
History
French physicist Charles-Augustin de Coulomb discovered in 1785 that the magnitude of electric force between two charged particles is directly proportional to the product of the absolute value of the two charges and inversely proportional to the distance squared between the two particles. He experimented with a torsion balance which consisted of an insulated bar suspended in the air by a silk thread. Coulomb attached a metal ball with a known charge to one end of the insulated bar. He then brought another ball with the same charge near the first ball. This distance between the two balls was recorded. The balls repelled each other, causing the silk thread to twist. The angle of the twist was measured and by knowing how much force was required for the thread to twist through the recorded angle, Coulomb was able to calculate the force between the two balls and derive the formula for electric force.
This video explains Coulomb's experiment and the corresponding derivation of his law.
See Also
Electric Field: [1]
Net Force: [2]
References
Matter & Interactions, Vol. II: Electric and Magnetic Interactions, 4th Edition
https://en.wikipedia.org/wiki/Coulomb's_law
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elefor.html