Point Charge
This page is all about the Electric Field due to a Point Charge.CLAIMED BY DEJAN TOJCIC 10-31-2016 == Electric Field==
A Work In Progress by Dejan Tojcic. dtojcic3 (talk)
The Main Idea
Looking at one of the four fundamental interactions of physics, electromagnetism, you can derive the expression for Coulombs Force Law. Using this expression, there is just a simple equation that is used to derive the the exact value of the electric field. The electric field of a point charge can be directly coordinated with a couple of independent variables. The variables that are directly coordinated with the value of an electric field is the direction of the particle and the charge of the particle. Electric field of a point charge is also inversely proportional to distance.
A Mathematical Model of Electric Field due to Point Charge
The Electric Field of a Point Charge can be found by using the following formula:
[math]\displaystyle{ \vec E=\frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} \hat r }[/math]
[math]\displaystyle{ Where \frac{1}{4 \pi \epsilon_0 } \text{is a constant representing the permittivity of free space, and is approximately } 9*10^{9} \frac{N m^2}{C^2} }[/math] , r is the magnitude of the distance between the observation location and the source location , q is the charge of the particle and [math]\displaystyle{ \hat r \text { is the direction of the distance from the source location to the observation point.} }[/math]
It is very easy to derive Coulombs Law using the equation for the electric field of a point charge, as all you have to do is multiply the value obtained from the Electric Field of a point charge by the charge of the second particle.
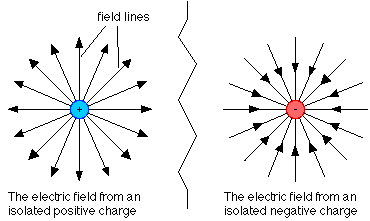
Below is a visual representation of electric fields due to a positive and negative point charge
A Computational Model
Here is a link to some code which can help visualize and compute the Electric Field due to an electron at different points. You can adjust the values of the observation locations in order to observe how the effects of distance, both magnitude and direction, can affect the electric field.
https://trinket.io/glowscript/8d66c87ced
<iframe src="https://trinket.io/embed/glowscript/8d66c87ced" width="100%" height="356" frameborder="0" marginwidth="0" marginheight="0" allowfullscreen></iframe>
Examples
Simple
There is an electron at <0,0,0>m. Calculate the electric field at <4,-3,1>m.
Step 1: Find [math]\displaystyle{ \hat r }[/math]
Find [math]\displaystyle{ \vec r_{obs} - \vec r_{electron} (\lt 4,-3,1\gt m - \lt 0,0,0\gt m = \lt 4,-3,1\gt m }[/math]
Calculate the magnitude of r. ([math]\displaystyle{ \sqrt{4^2+(-3)^2+1^2}=\sqrt{26} }[/math]
From r, find the unit vector [math]\displaystyle{ \hat{r}. }[/math] [math]\displaystyle{ \lt \frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}\gt }[/math]
Step 2: Find the magnitude of the Electric Field
[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} = \frac{1}{4 \pi \epsilon_0 } \frac{-1.6 * 10^{-19}}{26} }[/math]
Step 3: Multiply the magnitude of the Electric Field by [math]\displaystyle{ \hat{r} }[/math] to find the Electric Field
E= [math]\displaystyle{ \frac{1}{4 \pi \epsilon_0 } \frac{-1.6 * 10^{-19}}{26}*\lt \frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}\gt =\lt -4.34*10^{-11},3.26*10^{-11},-1.09*10^{-11}\gt N/C }[/math]
Middling
A particle of unknown charge is located at <-.21, .02, .11>m. Its electric field at point <-.02, .31, .28>m is <.124, .188, .109> N/C . Find the value of the particles charge.
While this problem looks challenging, lets think about it for a second. We are given both an observation location and a source location, so we can find both r and [math]\displaystyle{ \hat{r} }[/math] Since we are given the value of the electric field, we can simply find the magnitude of the electric field. Then, we can use the equation for the magnitude of electric field of a point charge,[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math] to find the charge.
Step 1: Find [math]\displaystyle{ \vec r_{obs} - \vec r_{particle} \lt -.02,.31,.28\gt m - \lt -.21,.02,.11\gt m = \lt .19,.29,.17\gt m }[/math]
To find r_{mag}, we simply find the magnitude of <.19,.29,.17>.
([math]\displaystyle{ \sqrt{.19^2+.29^2+.17^2}=\sqrt{.1491} }[/math]= .39
Step 2: Find the magnitude of the Electric Field
E= <.124, .188, .109> N/C
E_{mag} = ([math]\displaystyle{ \sqrt{.124^2+.188^2+.109^2}=\sqrt{.0626} }[/math]=.25
Step 3: Find q by rearranging the equation for E_{mag}
[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math]
By rearranging this equation we get
[math]\displaystyle{ q= {4 pi epsilon_0 } *{r^2}*E_{mag} }[/math]
[math]\displaystyle{ q= {1/(9*10^9)} *{.39^2}*.25 }[/math]
q= 4.3*10^-12 C
Difficult
The electric field at a location <.5.4, -1.8, 7.2>m has been found to be <5.5*10^3, -7.6*10^3, 0> N/C. There is a particle with a charge of -2nC in the surrounding area. What is the location of the particle?
Again, while at first sight the problem may look tough, it is really not that difficult once you break it down. Since we are given the vector value for electric field, we can also find the magnitude of the electric field. Once we find the magnitude of the electric field we can use the equation
[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r_{mag}^2} }[/math]
to find the rmag value. To find [math]\displaystyle{ \hat r }[/math] we can find the direction of the electric field as that is obviously going to be in the same direction as [math]\displaystyle{ \hat r }[/math]. Then, once we find [math]\displaystyle{ \hat r }[/math], all that is left to do is multiply [math]\displaystyle{ \hat r }[/math] by rmag and that will give us the [math]\displaystyle{ r }[/math] vector. We can then find the location of the particle as we know [math]\displaystyle{ r=r_{observation}-r_{particle} }[/math]
Step 1: Find the magnitude of the Electric field.
[math]\displaystyle{ E }[/math]= (5.5*10^3, -7.6*10^3, 0) N/C
[math]\displaystyle{ E_{mag} }[/math] = [math]\displaystyle{ \sqrt{(5.5*10^3)^2+(-7.6*10^3)^2+0^2}=\sqrt{.8.8*10^7}= 9381 }[/math]
Step 2:: Rearrange the equation for the magnitude of electric field and solve for rmag.
[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r_{mag}^2} }[/math]
[math]\displaystyle{ r_{mag}^2= \frac{1}{4 \pi \epsilon_0 } \frac{q}{ E_{mag}} }[/math]
[math]\displaystyle{ r_{mag}^2= \frac{1}{4 \pi \epsilon_0 } \frac{2nC}{ 9381} }[/math]
[math]\displaystyle{ r_{mag}^2= .00192 }[/math]
[math]\displaystyle{ r_{mag}= .04m }[/math]
Step 3: Find the direction of the electric field
Because the source charge is negative, [math]\displaystyle{ \hat r }[/math] [math]\displaystyle{ =-\hat E }[/math]
[math]\displaystyle{ \hat E }[/math] [math]\displaystyle{ = E/ E_{mag} }[/math]
[math]\displaystyle{ \hat E }[/math] [math]\displaystyle{ = (\lt 5.5*10^3, -7.6*10^3, 0\gt / 9381) N/C }[/math]
[math]\displaystyle{ \hat r }[/math] [math]\displaystyle{ =-\hat E }[/math] = <-.56, .81,0>
Step 4:
Connectedness
1.How is this topic connected to something that you are interested in?
I am very interested in the idea of forces and how objects interact with each other. After you calculate the Electric Field you can easily find the Electric Force one particle exerts on another.
2.How is it connected to your major?
I am a CompE major and so Electric Fields have to do with my major because when you integrate them with respect to dL, and swap the sign, you get potential difference(voltage), which is very important in circuits. As ECE majors take circuits classes, this topic is relevant to me.
3.Is there an interesting industrial application?
An interesting application is that electric fields of point charges can be used to find forces. Then you can predict the motion of various particles by the forces acting on them.
History
In the 1780s a French scientist named Charles Coulomb published many scientific papers on electricity and magnetism. While doing experiments, Coulomb had discovered an inverse square relationship between the amount of electric field and the distance between two particles and the electric field pointed in a line between the particles.
Also, he discovered that the charge of an particle (ie. positive or negative) determined the direction of the electric field (either a repulsion or attraction).
From these observations, as well as the use of fundamental constants, the equation of the electric field due to a point charge was created.
See also
Electric Field More general ideas about electric fields
Electric Force One application of electric fields due to point charges deals with finding electric force
Further reading
Principles of Electrodynamics by Melvin Schwartz ISBN: 9780486134673
External links
Some more information : http://hyperphysics.phy-astr.gsu.edu/hbase/electric/epoint.html
References
Matter and Interactions Vol. II
PY106 Notes. (n.d.). Retrieved November 27, 2016, from http://physics.bu.edu/~duffy/py106.html
Shech, E., & Hatleback, E. (n.d.). The Material Intricacies of Coulomb’s 1785 Electric Torsion Balance Experiment. Retrieved December 3, 2015, from http://philsci-archive.pitt.edu/11048/1/The_Material_Intricacies_of_Coulomb's_1785_Electric_Torsion_Balance_Experiment_(EV).pdf