System & Surroundings

Introduction: System, Surroundings, and Energy Accounting

Claimed by Hyder Hasnain When it comes to energy, choosing what is the system versus what is the surroundings greatly affects what needs to be accounted for when solving for various values. Choosing certain objects to be apart of the system rather than the surroundings can have an extreme effect on the outcome of said variables, especially when the surroundings do a fairly large amount of work on the system. By definition, a system is a specific part of the universe that we choose to study, while the surroundings are everything else that 'surrounds,' and typically has a significant effect on, the system. This page will analyze how different choices of systems can affect the components of the Energy Principle when relating it to the system.

The Energy Principle

To first understand the impact of the choice of system, it is best to fully understand the Energy Principle. The Energy Principle is based off of the fact that energy is a conserved quantity, meaning that it cannot be created nor destroyed. This definition of the conservation of energy gives the equation:

∆Esystem + ∆Esurroundings = 0

This best shows the idea that since energy is a conserved quantity, systems may only gain/lose energy if the surroundings lose/gain that same amount. This can be pictured in the image below.

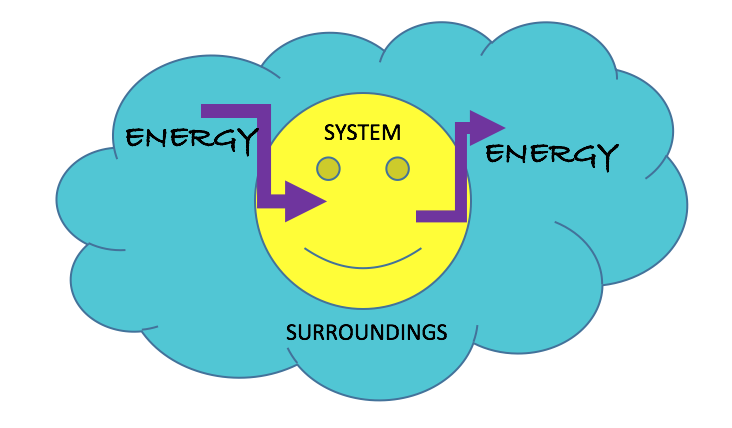
The Energy Principle can then be arranged by using the fact that the change in energy of a specific system is equal to the work done on the system by the surroundings.

∆Esystem = W

where ∆Esystem = Ef - Ei, making this equation now equal to:

Ef = Ei + W

The above equation will be what will primarily be used when accounting for all energy terms when the choice of system/surroundings changes.

Choice of System

Although physical results are always consistent, choosing different objects as the system changes the form of the energy equation that needs to be used, and which energy terms must be included in order to calculate accurate values for unknowns. In the following example, a fairly complex system will be analyzed in several different ways. Each of these will show a different choice of system and surroundings and how this effects the Energy Principle.

Example

In this example, a man is lifting his child in the air straight above his head as shown in the picture below. Two different choices of system will be analyzed, one in which the man, child, and Earth are all the system and the other where just the child is the system. By analyzing these two scenarios, it will become much clearer how the specific choice of system varies how equations are formed and calculations are carried out.

1) Man, Child, and the Earth

In this first situation, the system consists of the man, the child, and the Earth, while there is nothing deemed significant enough to include in the surroundings. In the intial state, the child is at rest, while in the final state the child has moved up above the man's head a distance, d, and has a specific velocity, v. Since there is nothing significant in the surroundings, the work is equal to 0. This gives the following equation:

Ef = Ei + W
Kf + Uf + Eman,f = Ki + Ui + Eman,i +W
Kf + mgd + Eman,f = 0 + 0 + Eman,i + 0
Eman,f - Eman,i = -(Kf + mgd)
∆Eman = -(Kf +mgd)

The formula for kinetic energy can then be used to solve for the change in energy of the man.

2) Child

In the second situation, the child is the only object in the system, which means that the man and the Earth are the surroundings. The initial and final conditions are the same as in the previous analysis, so the child still moves a distance upward, d, with velocity, v. The only difference is now that there are significant objects in the surroundings, the term for work is no longer equal to zero since both of these objects have an impact on the object. An equation for this situation can be found below:

Ef = Ei + W
Kf = Ki + Wman + W earth
Kf = 0 + Fd - mgd
Kf = Fd - mgd

By analyzing the systems/surroundings in these different ways, different variables can be found by relating the resulting equations to solve for unknowns. This sort of idea applies to many different situations involving energy, and it is very useful and necessary to be able to determine which factors must be included.

External links

Thinking about Physics Thinking by Professor Michael Schatz [1]

References

Matter and Interactions 4th Edition

Thinking about Physics Thinking

--Gnewville3 (talk) 22:39, 19 April 2016 (EDT)