Inelastic Collisions

This topic covers what inelastic collisions are, discusses a series of steps that can be undertaken to solve problems involving them, and then provides an example with the answers worked out. --Csorensen6 (talk) 21:06, 4 April 2016 (EDT)

Definition

Inelastic collisions differ from elastic collisions in one primary aspect: the initial kinetic energy is greater than the final kinetic energy. In other words, kinetic energy is NOT conserved, and Kf < Ki. Momentum, however, is still conserved, so Pf = Pi.

Moreover, because the final kinetic energy is less than the initial kinetic energy, inelastic collisions witness a change in the internal energy of the objects involved in the collision. A change in internal energy often manifests itself in the objects deforming, rotating, getting hot, vibrating, or being excited to a higher energy state.

The video linked below explores in further detail the differences between elastic and inelastic collisions, and it also provides some examples of each.

[1]

Maximally Inelastic Collisions

One of the most commonly-seen situations is the maximally inelastic collision, in which two objects collide and then stick together. The below image illustrates a maximally inelastic collision. More information about such problems can be found in the page about maximally inelastic collisions.

http://images.tutorvista.com/cms/images/83/inelastic-collision-image.gif

Typical Process for Solving

In such problems, it is often necessary to apply both the momentum principle and the energy principle. The image below provides an example of and the equations involved in solving a maximally inelastic collision problem. http://hyperphysics.phy-astr.gsu.edu/hbase/imgmec/inecol.gif

The steps for solving inelastic collision problems are often as follows:

1) Draw a picture of the initial and final states.

2) Given that collisions involve extremely large forces acting over short time intervals, it is accurate to say that Fnet,ext = 0, because the external forces are typically much, much smaller than the internal forces involved in the collision.

3) Knowing that Fnet,ext = 0, this means that momentum is conserved and that Pf = Pi. This comes from the momentum principle, in that ΔP = Fnet,ext*ΔT, and if Fnet,ext is zero, then the right side of that equation is also zero.

4) Next, knowing that Pf = Pi, you can solve for any unknown velocities of the objects involved via the momentum principle.

5) Having determined the velocity of each object, you can then determine the initial and final kinetic energies of the system using K = (1/2)*m*|v|^2 for each object.

6) Next, you can find the change in kinetic energy, or ΔK, and this will be equal to the change in the internal energy (whether it be heat, rotation, etc.) gained by the objects in the course of the collision.

Example Problem

Question

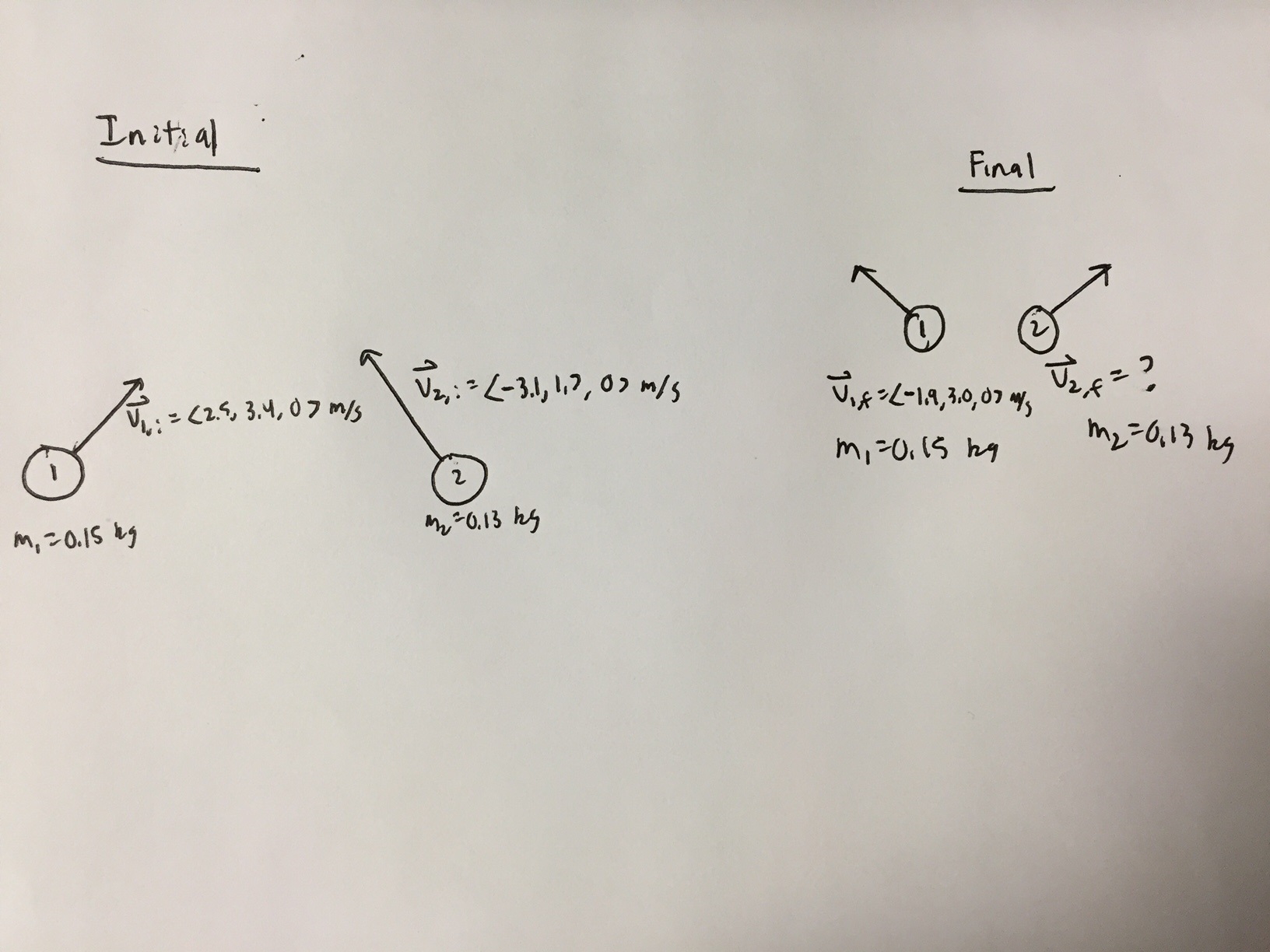
There are two hockey pucks traveling across the surface of a frozen pond. The first puck has a mass of 0.15 kg and is moving with a velocity of <2.5, 3.4, 0> m/s. The second puck has a mass of 0.13 kg and is moving with a velocity of <-3.1, 1.7, 0> m/s. After colliding, the first puck then has a velocity of <-1.9, 3.0, 0> m/s. (Reference the image below).

a) What is the velocity of the second puck after the collision?

b) What is the initial kinetic energy?

c) What is the final kinetic energy?

d) What is the change of the internal energy of the two pucks?

Answer

a) ΔP = Pf - Pi = Fnet,ext*ΔT = 0

  Pi = Pf

  0.15kg<2.5, 3.4, 0> m/s + 0.13kg<-3.1, 1.7, 0> m/s = 0.15kg<-1.9, 3.0, 0> m/s + 0.13kg*v
  <-0.028, 0.731, 0> kg*m/s = <-0.285, 0.45, 0> kg*m/s + 0.13kg*v
  <0.257,0.281,0> kg*m/s = 0.13kg*v
  v = <1.977, 2.162, 0> m/s

b) K = (1/2)*m*|v|^2

  |v| = (vx^2 + vy^2 + vz^2)^(1/2)      
  |v|^2 = vx^2 + vy^2 + vz^2
     
  Ki = (1/2)*0.15kg*((2.5 m/s)^2 + (3.4 m/s)^2 + (0 m/s)^2) + (1/2)*0.13kg*((-3.1 m/s)^2 + (1.7 m/s)^2 + (0 m/s)^2)
  Ki = 1.336 J + 0.813 J
  Ki = 2.149 J

c) K = (1/2)*m*|v|^2

  |v| = (vx^2 + vy^2 + vz^2)^(1/2)      
  |v|^2 = vx^2 + vy^2 + vz^2   

  Kf = (1/2)*0.15kg*((-1.9 m/s)^2 + (3.0 m/s)^2 + (0 m/s)^2) + (1/2)*0.13kg*((1.977 m/s)^2 + (2.162 m/s)^2 + (0 m/s)^2)
  Kf = 0.946 J + 0.558 J
  Kf = 1.504 J

d) ΔE = Q + W = ΔK + ΔEinternal + ΔU + ΔErest

  ΔE = ΔK + ΔEinternal = 0 = Kf - Ki + ΔEinternal

  1.504 J - 2.149 J + ΔEinternal = 0
  -0.645J + ΔEinternal = 0
  ΔEinternal = 0.645 J