Escape Velocity

From Physics Book
Revision as of 12:39, 2 December 2025 by Anguyen676 (talk | contribs) (I corrected several physics inaccuracies, including the incorrect claim of zero net force during escape and a wrong numerical value for the Moon’s escape velocity. I rewrote the introduction and mathematical model to clearly derive escape velocity using mechanical energy and to explain why gravitational force remains nonzero. I replaced vague or misleading examples with physics-appropriate problems and removed incorrect ones. The “Bound vs. Unbound” section was reorganized using total mechanical)
Jump to navigation Jump to search
A diagram showing the paths of Voyager 1 and 2.

Edited by Alexander Nguyen, Fall 2025

Escape velocity is the minimum initial speed required for an object to overcome the gravitational attraction of a massive body and reach an infinitely large distance without further propulsion. It is derived from conservation of mechanical energy. An object launched at escape speed will continue slowing due to gravity, but it will never reverse direction and fall back. Gravitational force and acceleration remain nonzero at all finite distances; only as [math]\displaystyle{ r \rightarrow \infty }[/math] do they approach zero.

The Main Idea

The formula for escape velocity at a given distance from a body is calculated by the formula

[math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}}, }[/math]

where [math]\displaystyle{ G }[/math] is the universal gravitational constant ([math]\displaystyle{ G = 6.67430\times 10^{-11}\,\text{m}^3\text{kg}^{-1}\text{s}^{-2} }[/math]), [math]\displaystyle{ M }[/math] is the mass of the large body to be escaped, and [math]\displaystyle{ r }[/math] the distance from the center of mass of the mass [math]\displaystyle{ M }[/math] to the object. This equation assumes there are no other forces acting on either body. As a side note, the escape velocity stated here could really be called escape speed due to the fact that the quantity is independent of direction. Notice that the equation does not include the mass of the orbiting body.

A Mathematical Model

The escape velocity condition is obtained from conservation of mechanical energy. Consider the system consisting of a planet of mass [math]\displaystyle{ M }[/math] and an object of mass [math]\displaystyle{ m }[/math] launched from radius [math]\displaystyle{ r }[/math].

Initial energy: [math]\displaystyle{ E_i = K_i + U_i = \frac{1}{2}mv_e^2 - \frac{GMm}{r} }[/math]

Final state at infinity: [math]\displaystyle{ K_f = 0,\quad U_f = 0 }[/math]

Thus, [math]\displaystyle{ E_i = E_f = 0 }[/math]

Solving, [math]\displaystyle{ \frac{1}{2}mv_e^2 - \frac{GMm}{r} = 0 }[/math]

[math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}} }[/math]

Because [math]\displaystyle{ m }[/math] cancels, escape velocity is independent of the mass of the escaping object. Only the central body mass and launch radius matter.

Bound versus unbound systems

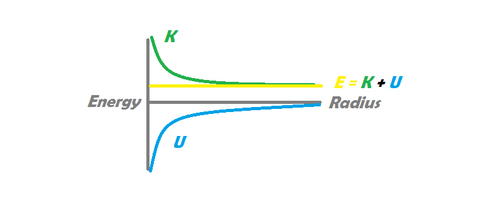
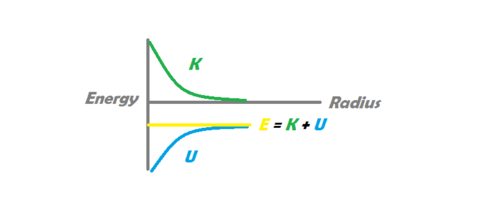
When an object is orbiting a massive body, it can be in one of two states: bound and unbound. If the object is in a bound state, we see an elliptical trajectory, in which the orbiting body never escapes the gravitational influence of the more massive body. In an unbound state, however, we observe a parabolic or hyperbolic trajectory, in which the object is able to escape the gravitational influence of the orbiting body and In a bound system, the total mechanical energy satisfies [math]\displaystyle{ E \lt 0 }[/math]. In a marginally unbound trajectory (parabolic), [math]\displaystyle{ E = 0 }[/math]. In a hyperbolic trajectory, [math]\displaystyle{ E \gt 0 }[/math]. The diagram to the left shows an unbound system, in which the sum of the kinetic and potential energy of the orbiting body is greater than 0. As distance goes to infinity in this system, gravitational potential energy approaches zero, but the object retains a positive kinetic energy, and therefore a positive velocity. The image on the right shows a bound system, in which the sum of the kinetic and potential energy is negative. In this system, kinetic energy reaches zero at a specific maximum distance, at which point the object begins to fall back towards the massive body, never to escape.

The energy diagram of an unbound system, in which the object has excess kinetic energy. The vertical axis represents energy, while the horizontal axis represents distance. At exactly the escape velocity, the sum of [math]\displaystyle{ K }[/math] and [math]\displaystyle{ U }[/math] is exactly 0.
The energy diagram of a bound system, in which the object has insufficient kinetic energy to escape. The vertical axis represents energy, while the horizontal axis represents distance.


A Computational Model

The PhET Gravity and Orbits simulation allows experimentation with orbital trajectories. To explore escape velocity:

  • Select the single planet–satellite system.
  • Place the satellite at a fixed launch radius.
  • Increase the initial launch speed gradually.
  • When the trajectory transitions from elliptical to open, the launch speed is equal to or greater than the escape velocity at that radius.

Compare this observed value to [math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}} }[/math].

Middling

Question 1

If the escape velocity of a planet with the same mass as Earth is greater than the escape velocity of Earth, is the planet larger or smaller than Earth?

Solution 1

Given the formula: [math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}} }[/math]

And rearranging for radius: [math]\displaystyle{ r = \frac{2GM}{v^2_e} }[/math]

We can see that since the denominator of the faction is larger with a constant numerator, then the radius must be smaller. Therefore, the planet is smaller than Earth.

Question 2

v = 4.76 m/s

Solution 2

The escape velocity is the minimum velocity required to escape the gravitational field of a planet, so the object must have kinetic energy greater than or equal to its potential energy.

34 = \frac{1}{2} m v^2 v^2 = (2*34)/3 v = 4.76 m/s

Difficult

Question 1

The radius of Jupiter is [math]\displaystyle{ 71.5\times 10^6 \text{m} }[/math], and its mass is [math]\displaystyle{ 1900\times 10^{24} \text{kg} }[/math]. What is the escape speed of an object launched straight up from just above the atmosphere of Jupiter?

Solution 1

System = Jupiter + object [math]\displaystyle{ \Delta E = 0\\ v_i = ?\\ v_f = 0 \text{m/s}\\ r_i = 71.5\times 10^6 \text{m}\\ r_f = \infty\\ m = m_{Object}\\ M = m_{Jupiter} = 1900\times 10^{24} \text{kg} \\ }[/math]

Starting from the Energy Principle:

[math]\displaystyle{ \Delta E = W + Q\\ \Delta E = 0 + 0 = 0\\ \Delta K + \Delta U = 0\\ \frac{1}{2}m(v_f^2-v_i^2) + (\frac{-GMm}{r_f} - \frac{-GMm}{r_i}) = 0\\ \frac{1}{2}m(0-v_i^2) + (0 - \frac{-GMm}{r_i}) = 0\\ -\frac{1}{2}mv_i^2 + \frac{GMm}{r_i} = 0\\ \frac{GMm}{r_i} = \frac{1}{2}mv_i^2\\ \frac{GM}{r_i} = \frac{1}{2}v_i^2\\ v_i = \sqrt{\frac{2GM}{r_i}}\\ = \sqrt{\frac{2(6.67430\times 10^{-11} \text{N}\cdot\text{m}^2 / \text{kg}^2)(1900\times 10^{24} \text{kg})}{(71.5\times 10^6 \text{m})}}\\ = 5.97 \times 10^4 \text{m/s} }[/math]

Question 2

Jupiter has 318 times the mass of the Earth, and its radius is 11.2 times that of the Earth. Calculate the escape velocity of a body from Jupiter’s surface assuming that the escape velocity from Earth’s surface is 11.2 Km/s.

Solution 2

[math]\displaystyle{ v_e = \sqrt{\frac{2GM_e}{r_e}}= 11.2 km/s }[/math]

[math]\displaystyle{ v_j = \sqrt{\frac{2GM_j}{r_j}} }[/math]

[math]\displaystyle{ M_j = 318M_e \text{ and } R_j = 11.2R_e }[/math]

Therefore,

[math]\displaystyle{ v_j = \sqrt{\frac{2G(318M_r)}{11.2R_e}} = 59.7 km/s }[/math]

Connectedness

In real life, escape velocity is not as easy to calculate as in the above examples. The primary complicating factor is the fact that there are more than two bodies in the universe, so in systems with multiple massive attracting bodies, escape velocity can become more complicated. One example is the escape velocity of an object from Earth: an object that achieves the escape velocity of Earth could theoretically escape Earth's influence, but it would remain in orbit around the sun unless its speed were much greater. The concept of escape velocity is widely used in orbital mechanics and rocketry and is critical for the planning of space missions.

History

Escape velocity stems from the concept of gravity, which was pioneered by Sir Issac Newton. Escape velocity became more important as people looked towards putting objects and people in space. Luna 1, launched in 1959 by the Soviets, was the first man-made object to surpass escape velocity from Earth.

See Also

Further Reading

https://www.nasa.gov/audience/foreducators/k-4/features/F_Escape_Velocity.html

http://www.qrg.northwestern.edu/projects/vss/docs/space-environment/2-whats-escape-velocity.html

https://www.sciencedirect.com/topics/engineering/escape-velocity.

External links

http://www.scientificamerican.com/article/bring-science-home-reaction-time/

https://www.youtube.com/watch?v=7w56rwAtUZU

References

“A Brief History of Space Exploration.” The Aerospace Corporation, The Aerospace Corporation, 1 June 2018, aerospace.org/article/brief-history-space-exploration.

"Escape Velocity | Physics." Encyclopedia Britannica Online. Encyclopedia Britannica, n.d. Web. 05 Dec. 2015. [1]

"Escape Velocity." Wikipedia. Wikimedia Foundation, n.d. Web. 05 Dec. 2015. [2]

“Escape Velocity Formula - with Solved Examples.” Physicscatalyst's Blog, 4 Nov. 2022, https://physicscatalyst.com/article/escape-velocity-formula/#.Y41KpuzMKrc.

Giancoli, Douglas C. "Physics for Scientists and Engineers with Modern Physics." Google Books. Google, n.d. Web. 05 Dec. 2015. [3]

“Gravity And Orbits.” PhET, University of Colorado Boulder, 5 Aug. 2019, phet.colorado.edu/en/simulation/gravity-and-orbits.

“Luna 1.” Wikipedia, Wikimedia Foundation, 15 Nov. 2022, https://en.wikipedia.org/wiki/Luna_1.

Velocity, Escape, and ©200. ESCAPE VELOCITY EXAMPLES (n.d.): n. pag. 13 June 2003. Web. 5 Dec. 2015. [4]

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Escape_Velocity&oldid=47669"