Escape Velocity

Edited by Engi Alabady, Fall 2022

Escape velocity is defined as the minimum velocity required for an object to escape the gravitational force of a large object. The sum of an object's kinetic energy and its gravitational potential energy is equal to zero. The gravitational potential energy is negative due to the fact that kinetic energy is always positive. The velocity of the object will be zero at infinite distance from the center of gravity. There is no net force on an object as it escapes and zero acceleration is perceived.Escape velocity can also be thought of as the energy needed for a large body to escape the gravitational field WITHOUT impulse.

The Main Idea

The formula for escape velocity at a given distance from a body is calculated by the formula

[math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}}, }[/math]

where [math]\displaystyle{ G }[/math] is the universal gravitational constant ([math]\displaystyle{ G = 6.7\times 10^{-11} \text{N}\cdot\text{m}^2 / \text{kg}^2 }[/math]), [math]\displaystyle{ M }[/math] is the mass of the large body to be escaped, and [math]\displaystyle{ r }[/math] the distance from the center of mass of the mass [math]\displaystyle{ M }[/math] to the object. This equation assumes there are no other forces acting on either body. As a side note, the escape velocity stated here could really be called escape speed due to the fact that the quantity is independent of direction. Notice that the equation does not include the mass of the orbiting body.

A Mathematical Model

When we model escape velocity, we consider the situation when an object's velocity takes it to a point an infinite distance away. The lowest possible escape velocity has a final speed of zero, and any speed higher results in a nonzero final speed. To derive the formula for the escape velocity, the energy principle is used, and we assume that the only two objects in our system are the orbiting body and the planet.

In our system, the energy principle states that

[math]\displaystyle{ (K + U_g)_i = (K + U_g)_f \, }[/math]

When finding the minimum escape velocity, [math]\displaystyle{ K-f = 0 }[/math] because we take the final velocity to be zero, and [math]\displaystyle{ U_{gf} = 0 }[/math] because its final distance is expressed as infinity, therefore

[math]\displaystyle{ (K + U_g)_i = \frac{1}{2}mv_e^2 + \frac{-GMm}{r} = 0 }[/math]

Solving for [math]\displaystyle{ v_e }[/math] yields:

[math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}} }[/math]

Note that because both the kinetic and potential energy terms contain a common factor [math]\displaystyle{ m }[/math], the final escape velocity is independent of the mass of the orbiting body.

Bound versus unbound systems

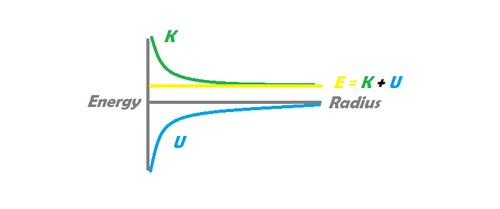
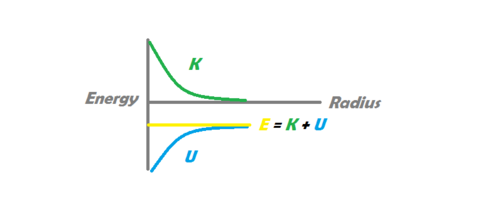
When an object is orbiting a massive body, it can be in one of two states: bound and unbound. If the object is in a bound state, we see an elliptical trajectory, in which the orbiting body never escapes the gravitational influence of the more massive body. In an unbound state, however, we observe a parabolic or hyperbolic trajectory, in which the object is able to escape the gravitational influence of the orbiting body and escape to infinity. The diagram to the left shows an unbound system, in which the sum of the kinetic and potential energy of the orbiting body is greater then 0. As distance goes to infinity in this system, gravitational potential energy approaches zero, but the object retains a positive kinetic energy, and therefore a positive velocity. The image on the right shows a bound system, in which the sum of the kinetic and potential energy is negative. In this system, kinetic energy reaches zero at a specific maximum distance, at which point the object begins to fall back towards the massive body, never to escape.

A Computational Model

Here is simulation that can be used to experiment with different factors that affect escape velocity:https://phet.colorado.edu/en/simulation/gravity-and-orbits.

Examples

Simple

Question 1

Compute the escape velocity for Earth if its mass is [math]\displaystyle{ 5.98 \times 10^{24} \text{kg} }[/math] and its radius is [math]\displaystyle{ 6.37 \times 10^{6} \text{m} }[/math].

Solution 2

[math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}} \\ = \sqrt{\frac{2(6.7\times 10^{-11} \text{N}\cdot\text{m}^2 / \text{kg}^2)(5.98\times 10^{24} \text{kg})}{(6.37\times 10^6 \text{m})}}\\ = 1.12 \times 10^4 \text{m/s} }[/math]

Question 2

Determine the escape velocity of the moon if mass is 7.35 × 10^22 kg and the radius is 1.5 × 10^6 m.

Solution 2

[math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}} \\ = \sqrt{\frac{2(6.7\times 10^{-11} \text{N}\cdot\text{m}^2 / \text{kg}^2)(7.35\times 10^{22} \text{kg})}{(1.5\times 10^6 \text{m})}}\\ = 7.59 \times 10^5 \text{m/s} }[/math]

Middling

Question 1

If the escape velocity of a planet with the same mass as Earth is greater than the escape velocity of Earth, is the planet larger or smaller than Earth?

Solution 1

Given the formula: [math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}} }[/math]

And rearranging for radius: [math]\displaystyle{ r = \frac{2GM}{v^2_e} }[/math]

We can see that since the denominator of the faction is larger with a constant numerator, then the radius must be smaller. Therefore, the planet is smaller than Earth.

Question 2

The potential energy of a 3kg mass on Earth is -34J. What will be its escape velocity?

Solution 2

The escape velocity is the minimum velocity required to escape the gravitational field of a planet, so the object must have kinetic energy greater than or equal to its potential energy.

34 = 1/2 * m * v^2 v^2 = (2*34)/3 v = 4.76 m/s

Difficult

Question 1

The radius of Jupiter is [math]\displaystyle{ 71.5\times 10^6 \text{m} }[/math], and its mass is [math]\displaystyle{ 1900\times 10^{24} \text{kg} }[/math]. What is the escape speed of an object launched straight up from just above the atmosphere of Jupiter?

Solution 1

System = Jupiter + object [math]\displaystyle{ \Delta E = 0\\ v_i = ?\\ v_f = 0 \text{m/s}\\ r_i = 71.5\times 10^6 \text{m}\\ r_f = \infty\\ m = m_{Object}\\ M = m_{Jupiter} = 1900\times 10^{24} \text{kg} \\ }[/math]

Starting from the Energy Principle:

[math]\displaystyle{ \Delta E = W + Q\\ \Delta E = 0 + 0 = 0\\ \Delta K + \Delta U = 0\\ \frac{1}{2}m(v_f^2-v_i^2) + (\frac{-GMm}{r_f} - \frac{-GMm}{r_i}) = 0\\ \frac{1}{2}m(0-v_i^2) + (0 - \frac{-GMm}{r_i}) = 0\\ -\frac{1}{2}mv_i^2 + \frac{GMm}{r_i} = 0\\ \frac{GMm}{r_i} = \frac{1}{2}mv_i^2\\ \frac{GM}{r_i} = \frac{1}{2}v_i^2\\ v_i = \sqrt{\frac{2GM}{r_i}}\\ = \sqrt{\frac{2(6.7\times 10^{-11} \text{N}\cdot\text{m}^2 / \text{kg}^2)(1900\times 10^{24} \text{kg})}{(71.5\times 10^6 \text{m})}}\\ = 5.97 \times 10^4 \text{m/s} }[/math]

Question 2

Jupiter has 318 times the mass of the Earth, and its radius is 11.2 times that of the Earth. Calculate the escape velocity of a body from Jupiter’s surface assuming that the escape velocity from Earth’s surface is 11.2 Km/s.

Solution 2

[math]\displaystyle{ v_e = \sqrt{\frac{2GM_e}{r_e}}= 11.2 km/s }[/math]

[math]\displaystyle{ v_j = \sqrt{\frac{2GM_j}{r_j}} }[/math]

[math]\displaystyle{ M_j = 318M_e \text{ and } R_j = 11.2R_e }[/math]

Therefore,

[math]\displaystyle{ v_j = \sqrt{\frac{2G(318M_r)}{11.2R_e}} = 59.7 km/s }[/math]

Question 3:

Compute the “escape” velocity for Earth if its mass is 5.98 x 1024 kg, its radius is 6.37 x 106

m, and G = 6.67 x 10-11 N-m2

/Kg2 . The abbreviation “N” represents Newton, a unit of force in the metric system. Using these constraints, the answers will be in m/s.

1.2523265x10 4 ≈ 1.12x10 The escape velocity for Earth is approximately 1.12 x 104

m/s.

Connectedness

In real life, escape velocity is not as easy to calculate as in the above examples. The primary complicating factor is the fact that there are more than two bodies in the universe, so in systems with multiple massive attracting bodies, escape velocity can become more complicated. One example is the escape velocity of an object from Earth: an object that achieves the escape velocity of Earth could theoretically escape Earth's influence, but it would remain in orbit around the sun unless its speed were much greater. The concept of escape velocity is widely used in orbital mechanics and rocketry and is critical for the planning of space missions.

History

Escape velocity stems from the concept of gravity, which was pioneered by Sir Issac Newton. Escape velocity became more important as people looked towards putting objects and people in space. Luna 1, launched in 1959 by the Soviets, was the first man-made object to surpass escape velocity from Earth.

“Escape Velocity Formula - with Solved Examples.” Physicscatalyst's Blog, 4 Nov. 2022, https://physicscatalyst.com/article/escape-velocity-formula/#.Y41KpuzMKrc.

Giancoli, Douglas C. "Physics for Scientists and Engineers with Modern Physics." Google Books. Google, n.d. Web. 05 Dec. 2015. [3]

“Gravity And Orbits.” PhET, University of Colorado Boulder, 5 Aug. 2019, phet.colorado.edu/en/simulation/gravity-and-orbits.

“Luna 1.” Wikipedia, Wikimedia Foundation, 15 Nov. 2022, https://en.wikipedia.org/wiki/Luna_1.

Escape Velocity

Contents

The Main Idea

A Mathematical Model

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See Also

Further Reading

External links

References

Navigation menu