Work/Energy

The Main Idea

Up until this point, we've worked in applying the Energy Principal in situations where there is no work. Therefore, the energy equation would reduce to (assuming theres no heat lost to surroundings) ΔE = 0 or E_system = E_surroundings. But what if there is work? In this section we will cover what work is and how we will use it.

Work is a movement of an object in the direction of the force applied to it. A person pushing a box, jogging to work, and pulling a wagon are all doing work. We will be using work in the context of The Energy Principal in a moment but first lets look at the mathematical definition of work.

A Mathematical Model

The best definition of work is as an integral. It can be expressed as: [math]\displaystyle{ \int{F}\, dx }[/math]. This is the integral (evaluated over bounds from initial to final position) of the force times the change in position.

Dot Products

A dot product is a mathematical operator that serves to multiply two vectors. It is crucial to the idea of work, because under a constant force, Work can be expressed as W = [math]\displaystyle{ \vec F }[/math] ∙ [math]\displaystyle{ \vec x }[/math].

Algebraic Computation

To compute the dot product of two vectors, multiply the first element in either vector together and add them all up.
For instance, <3,2,1> ∙ <5,6,7> could be written as (3*5)+(6*2)+(7*1) and would equal 15+12+7 = 34

Take note that taking the dot product of two vectors yields a scalar

Geometric Explanation

Taking the dot product of two vectors can give you a feel for the positions of those two vectors in space. For example, the dot product of two perpendicular vectors is zero.

Practice Problems

1) <34,2,7>∙<2,1,0>
2) <0,0,0>∙<930843029,43982048,43291>
3) <1,1,1,0,7,3,2>∙<2,4,2,5,7,8,0>

Answers:
1)69
2) 0
3)81

Under a constant force, this can be expressed as W = [math]\displaystyle{ \vec F }[/math] ∙ [math]\displaystyle{ \vec x }[/math]. This will often be the formula used in this course. Keep in mind that this is a dot product, so if these two vectors are perpendicular to one another, the dot product (and therefore the work) will equal zero. This is a key connection to be made about work.

A Computational Model

INSERT INFO ABOUT COMPUTATIONAL MODEL HERE

Examples

Easy: A jogger goes for a 3 mile jog around a lake averaging 3m/s. She starts and finishes at her home. How much work does she do?

Solution: The formula for work is (FORMULA). In this problem, the Δx is zero, because the jogger ends up at the same place she started. Therefore, the total work is zero.

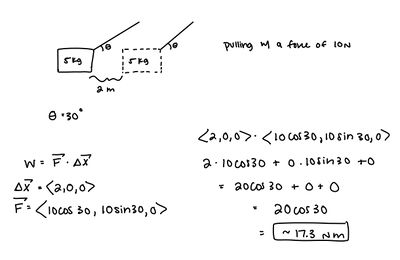
Medium: A 5kg box is dragged 2m across the floor with a rope pulling with a force of 10N at a 30 degree angle. How much work is done?
Solution:

Hard

ADD HARD EXAMPLE HERE

History

The concept of work is so fundamental to our modern understanding of physics that it is difficult to trace back its exact origins. It is thought, though that french mathematician Gaspard-Gustave Coriolis was the first to coin the term. At the time, he didn't understand the wide reaching applications of the term but used it nonetheless in a paper he published in 1835 to describe a force acting over a distance. Since that time, its mathematical and conceptual definition has become more complete and is pops up in many different disciplines from Classical Physics to Thermodynamics.

Gaspard-Gustave Coriolis
see citation 1

More Info

(1) https://www.britannica.com/biography/Gustave-Gaspard-Coriolis
(2) https://www.lindahall.org/gustave-coriolis/