Inclined Plane

Claimed by Catherine Grey Spring 2017

The Main Idea

An inclined plane is a flat surface that is higher on one end than the other... a real life right-triangle. Inclined planes are commonly used to move objects to a higher or lower place. These slopes lessen the force needed to move an object, but do require the object to be moved a greater distance, the hypotenuse of the triangular plane. Some examples of inclined planes include ramps, stairs, wedges (such as a door stopper), or even mountains which people sled down. To understand the motion of something moving along an inclined plane, forces may be taken into account using Newton's Laws, or the energy principle could be used if the object is moving or has a rotation.

A Mathematical Model

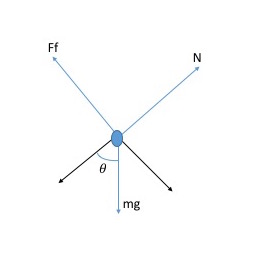
To obtain a mathematical model using Newton's Laws for an object on an inclined plane, it is easiest to construct a free body diagram with the object as the system. This figure showcases an example free body diagram. Most of the forces that could act on an inclined plane are shown. Depending on the question, all may or may not be present, especially friction.

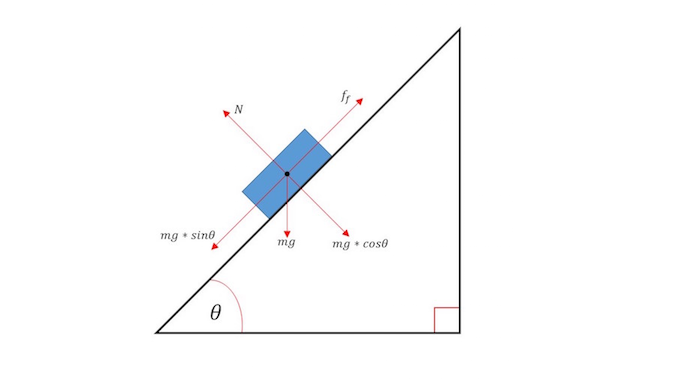
INSERT DRAWING

Variables:

[math]\displaystyle{ \theta = }[/math] Angle between the hypotenuse of the inclined plane and the horizontal

[math]\displaystyle{ \mathbf{g}= }[/math] Acceleration due to Gravity

[math]\displaystyle{ m = }[/math] Mass of the Object

[math]\displaystyle{ \mathbf{F_N} = }[/math] Normal Force (perpendicular to the plane)

[math]\displaystyle{ \mathbf{F_f} = }[/math] Frictional Force of the Inclined Plane (sometimes it is omitted)

[math]\displaystyle{ m g \ sin\theta = }[/math] A component force of gravity parallel to the plane (if [math]\displaystyle{ m \mathbf{g} \ sinθ \gt \mathbf{F_f} }[/math] the body slides down the plane)

[math]\displaystyle{ m g \ cos\theta = }[/math] A component force of gravity acting into the plane (opposite to [math]\displaystyle{ F_N }[/math])

Equations:

[math]\displaystyle{ \mathbf{F_{net}} = \sum \mathbf{F} = F_{net \ \parallel} + F_{net \ \perp} }[/math]

[math]\displaystyle{ F_{net//} = |\mathbf{F_f}| - mg \ sinθ }[/math]

[math]\displaystyle{ F_{netperp} = N - mg \ cosθ }[/math]

All energy equations are also present, especially when rotation is included on an inclined plane.

A Computational Model

Using GlowScript or VPython, we are able to model a box on an inclined plane moving upward with an initial velocity, then pulled downward as it is being affected by gravity. This code allows us to observe the final velocity, position, speed, and acceleration of the box.

Code

from __future__ import division
from visual import *
from visual.graph import *


scene.title = "Incline Plane"

scene.background = color.black scene.center = (0.7, 1, 0) # location at which the camera looks

inclinedPlane = box(pos = vector(0.6, 0, 0), size = (1.2, 0.02, 0.2), color = color.green, opacity = 0.3)

cart = box(size = (0.2, 0.06, 0.06), color = color.blue) # 20-cm long cart on the inclined plane

trail = curve(color = color.yellow, radius = 0.01) # units are in meters

cart.m = 0.5 # mass of cart in kg

cart.pos = vector(0, 0.04, 0.08)

cart.v = vector(0, 0, 0) # initial velocity of car in (vx, vy, vz) form, units are m/s

theta = 25.0 * (pi / 180.0)

inclinedPlane.rotate(angle = theta, origin = (0, 0, 0), axis = (0,0,1)) cart.rotate(angle = theta, origin = (0, 0, 0), axis = (0,0,1))

cart.v = norm(inclinedPlane.axis) cart.v.mag = 3

g = 9.8 # acceleration due to gravity; units are m/s/s

mu = 0.20 # coefficient of friction between cart and plane

t = 0 #starting time deltat = 0.0005 # time step units are s

print "initial cart position (m): ", cart.pos

while cart.pos.y > 0.02 :

   rate(1000)    
   Fnet = norm(inclinedPlane.axis)
   
   Fnet.mag = -(cart.m * g * sin(theta))
   
   if cart.v.y > 0:
       Fnet.mag += (mu * cart.m * g * cos(theta))
   else:
       Fnet.mag -= (mu * cart.m * g * cos(theta))
   
   cart.v = cart.v + (Fnet/cart.m * deltat)

   cart.pos = cart.pos + cart.v * deltat

   trail.append(pos = cart.pos)
  
   t = t + deltat
       

print "final time (s): ", t print "final cart position (m): ", cart.pos print "final cart velocity (m/s): ", cart.v print "final cart speed (m/s): ", mag(cart.v) print "final cart acceleration (m/s/s): ", (mag(Fnet) / cart.m)

Examples

The easiest example of an object on an inclined plane is removing all forces, but gravity. Since gravity is the only force acting on the object then the computations are easier. To make inclined plane problems harder, adding more forces or calculating for factors other than net force can be included, such as finding the acceleration or time it takes for the block to go from the top to the bottom of an inclined plane. As well, adding in rotation, with a ball rolling down the plane, would demonstrate other difficulties.

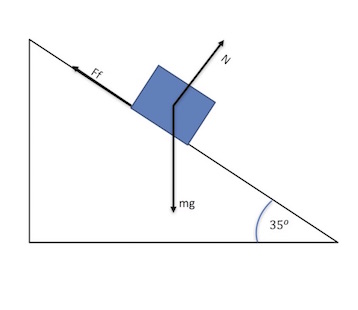
Easy

INSERT DRAWING

Above a 2.5 kg block slides down a plane inclined at an angle of 35 degrees to the horizontal. The coefficient of kinetic friction is 0.14.

a) Draw a free-body diagram for the block.

INSERT DRAWING

b) Determine the normal force exerted on the block.

[math]\displaystyle{ \mathrm{N} = mgCosθ \, }[/math]

[math]\displaystyle{ \mathrm{N} = 2.5*9.8*Cos35 \, }[/math]

[math]\displaystyle{ \mathrm{N} = 20 N \, }[/math]

c) Determine the force of kinetic friction.

[math]\displaystyle{ \mathrm{F_f} = mu*N \, }[/math]

[math]\displaystyle{ \mathrm{F_f} = .14*20 \, }[/math]

[math]\displaystyle{ \mathrm{F_f} = 2.8 N \, }[/math]

d) Determine the acceleration of the block.

[math]\displaystyle{ \mathrm{F_y} = N- mgCosθ = 0 \, }[/math]

[math]\displaystyle{ \mathrm{F_x} = mgSinθ - F_ f = ma_x\, }[/math]

[math]\displaystyle{ \mathrm{a_x} = \frac {mgSinθ - F_ f }{m}\, }[/math]

[math]\displaystyle{ \mathrm{a_x} = \frac {24.5*Sin35 - 2.8}{2.5} \, }[/math]

[math]\displaystyle{ \mathrm{a_x} = 4.5 m/s^2 \, }[/math]

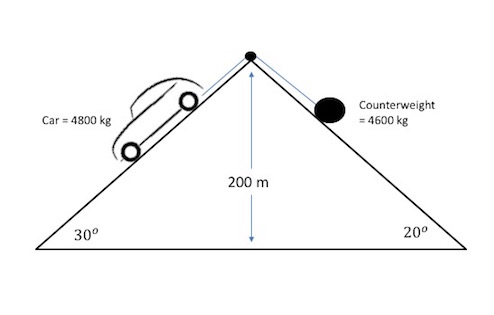
Medium

The Figure above shows a 4800 kg car descending a hill. A counterweight of mass 4600 kg on the other side of the hill helps the breaks slow the car down. The rolling friction of both the car and the counterweight are negligible. How much braking force does the cable car need to descend at constant speed?

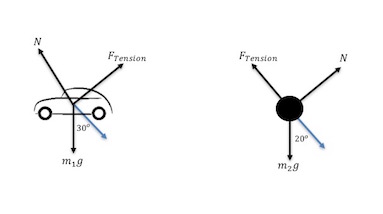
First, draw free-body diagrams:

Car:

[math]\displaystyle{ \mathrm{F_x} = T + (-m_1gSinθ) + (-F_{brakes}) = 0 \, }[/math]

[math]\displaystyle{ \mathrm{F_{brakes}} = T + (-m_1gSinθ) \, }[/math]

Counterweight:

[math]\displaystyle{ \mathrm{F_x} = T + (-m_2gSinθ) = 0 \, }[/math]

[math]\displaystyle{ \mathrm{T} = m_2gSinθ \, }[/math]

Then combine both equations:

[math]\displaystyle{ \mathrm{F_{brakes}} = m_1gSinθ - m_2gSinθ \, }[/math]

[math]\displaystyle{ \mathrm{F_{brakes}} = 4600*9.8Sin20 - 4800*9.8Sin30 \, }[/math]

[math]\displaystyle{ \mathrm{F_{brakes}} = 8100 N \, }[/math]

Hard

A ball rolls down the inclined plane in the figure above. Determine the final velocity (in terms of variables) of the ball at the end of the incline. Assume there is no change in temperature of the ball.

[math]\displaystyle{ \triangle E = W + 0 \, }[/math]

[math]\displaystyle{ \triangle K_{trans} + \triangle K_{rot} = h*m*g + 0 \, }[/math]

[math]\displaystyle{ \triangle K_{trans} + \triangle K_{rot} = h*m*g + 0 \, }[/math]

[math]\displaystyle{ \mathrm{0.5*m*(v_f)^2 + 0.5*I*(w_f)^2} = h*m*g \, }[/math]

We know the moment of Inertia I for a ball or sphere is:

[math]\displaystyle{ \ I = (2/5)*m*R^2 \, }[/math]

And:

[math]\displaystyle{ \ {w_f} = \frac{v_f}{R} \, }[/math]

So:

[math]\displaystyle{ \ 0.5*m*(v_f)^2 + 0.5*I*(\frac{v_f}{R})^2 = h*m*g \, }[/math]

[math]\displaystyle{ \ 0.5*m*(v_f)^2 + 0.5*(2/5)*m*R^2 *(\frac{v_f}{R})^2 = h*m*g \, }[/math]

[math]\displaystyle{ \ 0.5*(v_f)^2 + 0.5*(2/5) *(v_f)^2 = h*g \, }[/math]

[math]\displaystyle{ \ (9/10)*(v_f)^2 = h*g \, }[/math]

[math]\displaystyle{ \ (v_f)^2 = h*g*(10/9) \, }[/math]

[math]\displaystyle{ \ (v_f) = \sqrt{h*g*(10/9)} \, }[/math]

Technical Usage

Terminology

Let's imagine there is a right triangle. The side opposite to the right angle is a Slant. The side on the bottom is Run. The side vertical to the bottom is Rise.

Slope: A slope brings a mechanical advantage to the incline plane.

[math]\displaystyle{ \theta = \tan^{-1} \bigg( \frac {\text{Rise}}{\text{Run}} \bigg) \, }[/math]

Mechanical Advantage

Fw is a gravitational force that applies on the plane
Fi is a force exerted on the object and parallel to the plane

[math]\displaystyle{ \mathrm{MA} = \frac{F_w}{F_i}. \, }[/math]

if the inclined plane is frictionless,

[math]\displaystyle{ \text{MA} = \frac{F_w}{F_i} = \frac {1}{\sin \theta} \, }[/math] (in this case, [math]\displaystyle{ \sin \theta = \frac {\text{Rise}}{\text{Length}} \, }[/math])

if the inclined plane has a friction

[math]\displaystyle{ \mathrm{MA} = \frac {F_w}{F_i} = \frac {\cos \phi} { \sin (\theta - \phi ) } \, }[/math] (in this case, [math]\displaystyle{ \phi = \tan^{-1} \mu \, }[/math])

[math]\displaystyle{ \theta \lt \phi\, }[/math]: Downhill applied force is needed.

[math]\displaystyle{ \theta = \phi\, }[/math]: Infinite mechanical advantage.

[math]\displaystyle{ \theta \gt \phi\, }[/math]: The mechanical advantage is positive. Uphill force is needed.

History

Archimedes

An inclined plane is one of the six classical simplified machines defined by Renaissance scientists. They have been used for thousands of years to move large objects to a specific distance, such as with the potential creation Stonehenge or the formation of the Egyptian Pyramids. In the second century B.C., Archimedes began theorizing some of the properties associated with an inclined plane including its various applications. Then in the first century A.D., Hero of Alexandria went beyond Archimedes initial theories to further explain the functionality of an inclined plane. These theories then proved to be a reality as the years went on and there were more advancements and functions applied to inclined planes.

Connectedness

Every day people experience some sort of inclined plane. From driving up a hill on the way to work to walking down a ramp to get to class (because of all of the construction we always have) an inclined plane is a vital piece of our lives. What I find the most interesting about inclined planes is how people use them and physics for fun without even knowing it. Such as going down a slide at a park or skiing down a snowy mountain, the physics and forces behind an inclined plane bring enjoyment to many people's lives every day.

An inclined plane relates to mechanical engineering because MEs will always be working with various systems including some form of an inclined plane. Such as pulling an object across a ramp or the mechanics behind a water slide at an amusement park, inclined planes are everywhere. The best advice is to become comfortable with how they work and how to calculate the net force acting on the object sitting or moving on the inclined plane.

See Also

Free Body Diagram
Normal Force

References

Cole, Matthew (2008). Explore science, 2nd Ed. Pearson Education. https://books.google.com/books?id=RhuciGEQ1G8C&pg=PA178#v=onepage&q&f=false

http://hyperphysics.phy-astr.gsu.edu/hbase/Mechanics/incline.html