Inclined Plane

Claimed by Catherine Grey Spring 2017

The Main Idea

A Mathematical Model

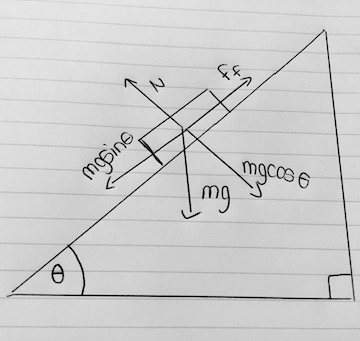
θ = Angle of the plane to the horizontal
g = Acceleration due to gravity
m = Mass of object
N = Normal force (perpendicular to the plane)
F_f = frictional force of the inclined plane (sometimes it is omitted on test problems)
mgSinθ = A force parallel to the plane (mgSinθ > Ff the body slides down the plane)
mgCosθ = A force acting into the plane (opposite to N)

F_netparallel = The net parallel force acting on the object
F_{netperpendiculr} = The net perpendicular force acting on the object

[math]\displaystyle{ \ Fnet_{//} = F_f - mgSinθ }[/math]

[math]\displaystyle{ \ Fnet_{perp} = N -mgCosθ }[/math]

Uses

You may see this almost every day in your daily life. The inclined planes are needed for loading and unloading heavy goods on transportation such as ships, trucks and planes because it has mechanical advantage of reducing the forces required to move heavy goods.

Terminology

Let's imagine there is a right triangle. The side opposite to the right angle is a Slant. The side on the bottom is Run The side vertical to the bottom is Rise

Slope: A slope brings a mechanical advantage to the incline plane.

[math]\displaystyle{ \theta = \tan^{-1} \bigg( \frac {\text{Rise}}{\text{Run}} \bigg) \, }[/math]

Mechanical Advantage

Fw is a gravitational force that applies on the plane
Fi is a force exerted on the object and parallel to the plane

[math]\displaystyle{ \mathrm{MA} = \frac{F_w}{F_i}. \, }[/math]

if the inclined plane is frictionless,

[math]\displaystyle{ \text{MA} = \frac{F_w}{F_i} = \frac {1}{\sin \theta} \, }[/math] (in this case, [math]\displaystyle{ \sin \theta = \frac {\text{Rise}}{\text{Length}} \, }[/math])

if the inclined plane has a friction

[math]\displaystyle{ \mathrm{MA} = \frac {F_w}{F_i} = \frac {\cos \phi} { \sin (\theta - \phi ) } \, }[/math] (in this case, [math]\displaystyle{ \phi = \tan^{-1} \mu \, }[/math])

[math]\displaystyle{ \theta \lt \phi\, }[/math]: Downhill applied force is needed.

[math]\displaystyle{ \theta = \phi\, }[/math]: Infinite mechanical advantage.

[math]\displaystyle{ \theta \gt \phi\, }[/math]: The mechanical advantage is positive. Uphill force is needed.

See Also

Free Body Diagram
Normal Force

References

http://www.newworldencyclopedia.org/entry/Inclined_plane
http://www.dictionary.com