Electric Force: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
claimed for editing and additional examples- Samuel Boyce Fall 2016 | claimed for editing and additional examples- Samuel Boyce Fall 2016 | ||
This page contains information on the electric force on a point charge. Electric force is created by an external [[Electric Field]], and the strength of this electrical interaction is a vector quantity that has magnitude and direction. If the electric field at a particular location is known, then this field can be used to calculate the electric force of the particle being acted upon. The electric force is directly proportional to the amount of charge within each particle being acted upon by the other's electric field. Moreover, the magnitude of the force is inversely proportional to the square distance between the two interacting particles. It is important to remember that a particle cannot have an electric force on itself; there must be at least two interacting, charged components. | This page contains information on the electric force on a point charge. Electric force is created by an external [[Electric Field]], and the strength of this electrical interaction is a vector quantity that has magnitude and direction. If the electric field at a particular location is known, then this field can be used to calculate the electric force of the particle being acted upon. The electric force is directly proportional to the amount of charge within each particle being acted upon by the other's electric field. Moreover, the magnitude of the force is inversely proportional to the square distance between the two interacting particles. It is important to remember that a particle cannot have an electric force on itself; there must be at least two interacting, charged components. | ||
==The Coulomb Force Law | ==The Main Idea== | ||
===A Mathematical Model=== | |||
The Coulomb Force Law | |||
The formula for the magnitude of the electric force between two point charges is: | The formula for the magnitude of the electric force between two point charges is: | ||
| Line 16: | Line 16: | ||
Interestingly enough, one can see a relationship between this formula and the formula for gravitational force (<math>F={G} \frac{|{m}_{1}{m}_{2}|}{r^2} </math>). From this relationship, one can conclude that the interactions of two objects as a result of their charges or masses follow similar fundamental laws of physics. | Interestingly enough, one can see a relationship between this formula and the formula for gravitational force (<math>F={G} \frac{|{m}_{1}{m}_{2}|}{r^2} </math>). From this relationship, one can conclude that the interactions of two objects as a result of their charges or masses follow similar fundamental laws of physics. | ||
'''Derivations of Electric Force''' | |||
The electric force on a particle can also be written as: | The electric force on a particle can also be written as: | ||
| Line 37: | Line 30: | ||
The units of charge are in Coulombs and the units for electric field are in Newton/Coulombs, so this derivation is correct in its dimensions since multiplying the two units gives just Newtons. The Newton is the unit for electric force. | The units of charge are in Coulombs and the units for electric field are in Newton/Coulombs, so this derivation is correct in its dimensions since multiplying the two units gives just Newtons. The Newton is the unit for electric force. | ||
==A Computational Model== | |||
===A Computational Model=== | |||
Direction of the Electric Force | |||
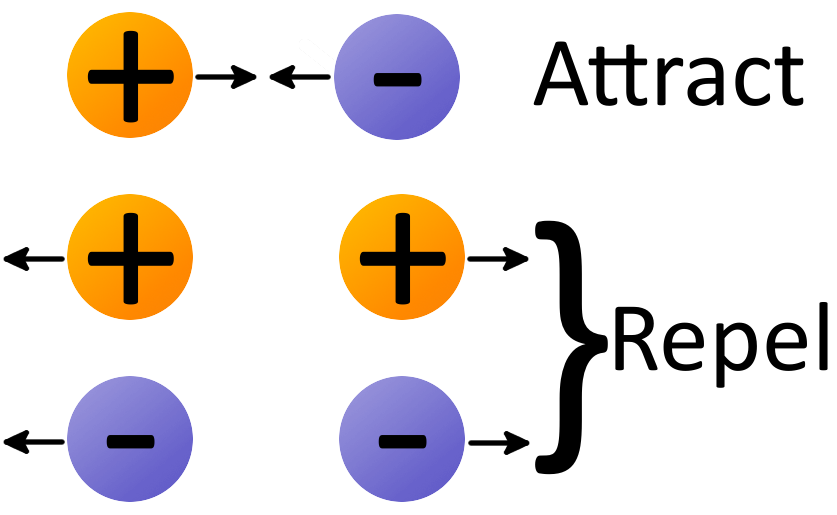
The electric force is along a straight line between the two point charges in the observed system. If the point charges have the same sign (i.e. both are either positively or negatively charged), then the charges repel each other. If the signs of the point charges are different (i.e. one is positively charged and one is negatively charged), then the point charges are attracted to each other. The electric force vector acts either in the same or opposite direction of the electric field acting on a particle, depending on the charge of that particle. Remember that negative charges attract, so the electric field of a negative charge will act from the observation location towards the charged negatively charged particle. If the observation particle is positively charged, then the electric force will act in the same direction as the electric field. If the observation particle is negatively charged, then the force will act in the opposite direction as the electric field. The same concepts apply to positive electric fields, which point away from the source location at the observation location. | |||
[[File:WhatisAnElectricForce.png]] | |||
==Examples== | ==Examples== | ||
=== | ===Simple=== | ||
'''Problem: '''Find the electric force of a -3 C particle in a region with an electric field of <math><7, 5, 0></math>N/C. | |||
'''Step 1: '''Substitute values into the correct formula. | |||
<math>\vec F=q\vec E </math> | |||
<math>\vec F=(-3 C)<7, 5, 0></math>N/C | |||
<math>\vec F=<-21, -15, 0></math>N | |||
The electric force vector for this particle is <math><-21, -15, 0></math>N. | |||
===Middling=== | |||
'''Problem: '''Find the magnitude of electric force on two charged particles located at <math> <0, 0, 0></math>m and <math> <0, 10, 0></math>m. The first particle has a charge of +5 nC and the second particle has a charge of -10 nC. Is the force attractive or repulsive? | '''Problem: '''Find the magnitude of electric force on two charged particles located at <math> <0, 0, 0></math>m and <math> <0, 10, 0></math>m. The first particle has a charge of +5 nC and the second particle has a charge of -10 nC. Is the force attractive or repulsive? | ||
| Line 54: | Line 65: | ||
<math>|\vec F|=\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}{q}_{2}|}{r^2}=\frac{1}{4 \pi \epsilon_0 } \frac{|(5 nC)(-10 nC)|}{(10m)^2} </math> | <math>|\vec F|=\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}{q}_{2}|}{r^2}=\frac{1}{4 \pi \epsilon_0 } \frac{|(5 nC)(-10 nC)|}{(10m)^2} </math> | ||
<math>|\vec F|=4.5e-9 </math> N | <math>|\vec F|=4.5e-9 </math> N | ||
| Line 64: | Line 74: | ||
Since the first particle is positively charged and the second is negatively charged, the force is attractive. The particles are attracted to each other. | Since the first particle is positively charged and the second is negatively charged, the force is attractive. The particles are attracted to each other. | ||
=== | ===Difficult=== | ||
Problem: | |||
[[File:SpringTest1Prob1.png]] | |||
==Connectedness== | ==Connectedness== | ||
| Line 97: | Line 94: | ||
https://en.wikipedia.org/wiki/Coulomb's_law | https://en.wikipedia.org/wiki/Coulomb's_law | ||
=Images= | |||
Electric Force Direction: http://blog.omninox.org/what-is-an-electric-force-2/ | |||
[[Category:Which Category did you place this in?]] | [[Category:Which Category did you place this in?]] | ||
Revision as of 16:17, 25 November 2016
--Asaxon7 (talk) 00:48, 18 November 2015 (EST) Claimed by Alayna Saxon
claimed for editing and additional examples- Samuel Boyce Fall 2016
This page contains information on the electric force on a point charge. Electric force is created by an external Electric Field, and the strength of this electrical interaction is a vector quantity that has magnitude and direction. If the electric field at a particular location is known, then this field can be used to calculate the electric force of the particle being acted upon. The electric force is directly proportional to the amount of charge within each particle being acted upon by the other's electric field. Moreover, the magnitude of the force is inversely proportional to the square distance between the two interacting particles. It is important to remember that a particle cannot have an electric force on itself; there must be at least two interacting, charged components.
The Main Idea
A Mathematical Model
The Coulomb Force Law The formula for the magnitude of the electric force between two point charges is:
[math]\displaystyle{ F=\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}{q}_{2}|}{r^2} }[/math]
where [math]\displaystyle{ {q}_{1} }[/math] and [math]\displaystyle{ {q}_{2} }[/math] are the magnitudes of charge of point 1 and point 2 and [math]\displaystyle{ r }[/math] is the distance between the two point charges. The units for electric force are in Newtons. The expression [math]\displaystyle{ \frac{1}{4 \pi \epsilon_0 } }[/math] is known as the electric constant and carries the value 9e9.
Interestingly enough, one can see a relationship between this formula and the formula for gravitational force ([math]\displaystyle{ F={G} \frac{|{m}_{1}{m}_{2}|}{r^2} }[/math]). From this relationship, one can conclude that the interactions of two objects as a result of their charges or masses follow similar fundamental laws of physics.
Derivations of Electric Force
The electric force on a particle can also be written as:
[math]\displaystyle{ \vec F=q\vec E }[/math]
where [math]\displaystyle{ q }[/math] is the charge of the particle and [math]\displaystyle{ \vec E }[/math] is the external electric field.
This formula can be derived from [math]\displaystyle{ |\vec F|=\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}{q}_{2}|}{r^2} }[/math], the electric force between two point charges. The magnitude of the electric field created by a point charge is [math]\displaystyle{ |\vec E|=\frac{1}{4 \pi \epsilon_0 } \frac{|q|}{r^2} }[/math], where [math]\displaystyle{ q }[/math] is the magnitude of the charge of the particle and [math]\displaystyle{ r }[/math] is the distance between the observation location and the point charge. Therefore, the magnitude of electric force between point charge 1 and point charge 2 can be written as:
[math]\displaystyle{ |\vec F|=\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}{q}_{2}|}{r^2}=|{q}_{2}|\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}|}{r^2}=|{q}_{2}||\vec{E}_{1}| }[/math]
The units of charge are in Coulombs and the units for electric field are in Newton/Coulombs, so this derivation is correct in its dimensions since multiplying the two units gives just Newtons. The Newton is the unit for electric force.
A Computational Model
Direction of the Electric Force The electric force is along a straight line between the two point charges in the observed system. If the point charges have the same sign (i.e. both are either positively or negatively charged), then the charges repel each other. If the signs of the point charges are different (i.e. one is positively charged and one is negatively charged), then the point charges are attracted to each other. The electric force vector acts either in the same or opposite direction of the electric field acting on a particle, depending on the charge of that particle. Remember that negative charges attract, so the electric field of a negative charge will act from the observation location towards the charged negatively charged particle. If the observation particle is positively charged, then the electric force will act in the same direction as the electric field. If the observation particle is negatively charged, then the force will act in the opposite direction as the electric field. The same concepts apply to positive electric fields, which point away from the source location at the observation location.
Examples
Simple
Problem: Find the electric force of a -3 C particle in a region with an electric field of [math]\displaystyle{ \lt 7, 5, 0\gt }[/math]N/C.
Step 1: Substitute values into the correct formula.
[math]\displaystyle{ \vec F=q\vec E }[/math]
[math]\displaystyle{ \vec F=(-3 C)\lt 7, 5, 0\gt }[/math]N/C
[math]\displaystyle{ \vec F=\lt -21, -15, 0\gt }[/math]N
The electric force vector for this particle is [math]\displaystyle{ \lt -21, -15, 0\gt }[/math]N.
Middling
Problem: Find the magnitude of electric force on two charged particles located at [math]\displaystyle{ \lt 0, 0, 0\gt }[/math]m and [math]\displaystyle{ \lt 0, 10, 0\gt }[/math]m. The first particle has a charge of +5 nC and the second particle has a charge of -10 nC. Is the force attractive or repulsive?
Step 1: Find the distance between the two point charges.
[math]\displaystyle{ d=\sqrt{(0 m-0 m)^2+(0 m-10 m)^2+(0 m-0 m)^2}=\sqrt{100 m}=10 }[/math]m.
The distance between the two points is 10 m.
Step 2: Substitute values into the correct formula.
[math]\displaystyle{ |\vec F|=\frac{1}{4 \pi \epsilon_0 } \frac{|{q}_{1}{q}_{2}|}{r^2}=\frac{1}{4 \pi \epsilon_0 } \frac{|(5 nC)(-10 nC)|}{(10m)^2} }[/math]
[math]\displaystyle{ |\vec F|=4.5e-9 }[/math] N
The magnitude of electric force is [math]\displaystyle{ |\vec F|=4.5e-9 }[/math] N.
Step 3: Determine if force is attractive or repulsive.
Since the first particle is positively charged and the second is negatively charged, the force is attractive. The particles are attracted to each other.
Difficult
Connectedness
History
French physicist Charles-Augustin de Coulomb discovered in 1785 that the magnitude of electric force between two charged particles is directly proportional to the product of the absolute value of the two charges and inversely proportional to the distance squared between the two particles. He experimented with a torsion balance which consisted of an insulated bar suspended in the air by a silk thread. Coulomb attached a metal ball with a known charge to one end of the insulated bar. He then brought another ball with the same charge near the first ball. This distance between the two balls was recorded. The balls repelled each other, causing the silk thread to twist. The angle of the twist was measured and by knowing how much force was required for the thread to twist through the recorded angle, Coulomb was able to calculate the force between the two balls and derive the formula for electric force.
See also
External links
http://www.physicsclassroom.com/class/estatics/Lesson-3/Coulomb-s-Law
References
Matter & Interactions, Vol. II: Electric and Magnetic Interactions, 4th Edition
https://en.wikipedia.org/wiki/Coulomb's_law
Images
Electric Force Direction: http://blog.omninox.org/what-is-an-electric-force-2/