Perpetual Freefall (Orbit): Difference between revisions
No edit summary |
|||
| Line 17: | Line 17: | ||
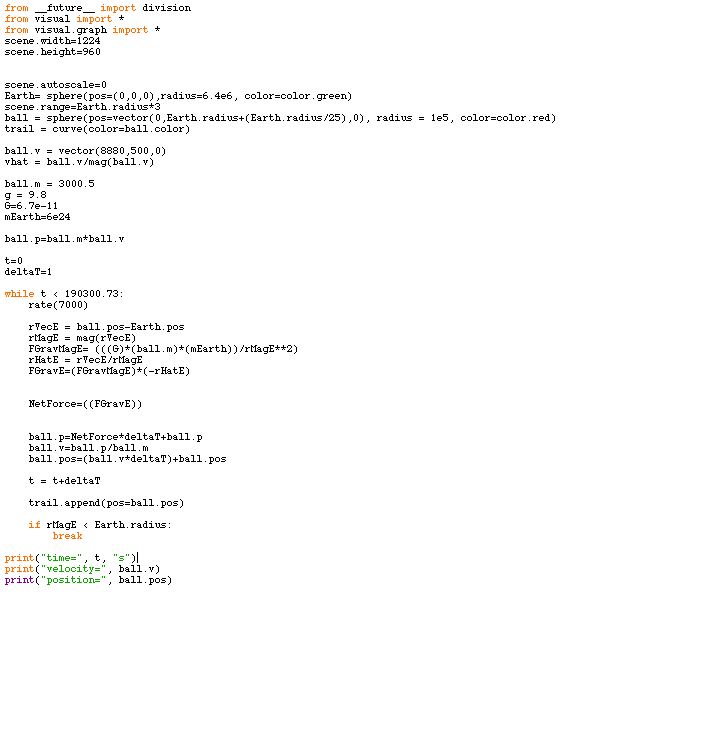
Below is the computational code written in vPython language. The code consists of a setup of the scene, initial conditions and constants, calculation of force, and an update of momentum, velocity and position. All of these components are expressed visually as a simulation. | Below is the computational code written in vPython language. The code consists of a setup of the scene, initial conditions and constants, calculation of force, and an update of momentum, velocity and position. All of these components are expressed visually as a simulation. | ||
[[File:CodeOrbit.png | vPython Code]] | |||
==Examples== | ==Examples== | ||
Revision as of 23:19, 5 December 2015
The concept of perpetual free fall extenuates from the idea that an object in space has enough directional velocity to overcome the gravitational force on that object by a larger body. When an objects velocity acts in this way, the object enters into a perpetual free fall or an orbit.
The Main Idea
For many objects, one of the main forces acting on them in a normal state is gravity. For organizations such as NASA or Boeing that utilize satellites around earth, gravity must be overcome to exit the lower atmospheric atmospheres and to maintain their technologies stay in flight around the earth. Entering an object into an orbit is the only way to overcome the effects of gravity and prevent it from returning to the Earth's surface. This is achieved via perpendicular propulsion and altitude adjustment in lower atmospheres where air resistance in present, or is achieved by achieving a high enough stable velocity outside the Earth's atmosphere. By producing enough perpendicular velocity, the object travels beyond the curve of the planet before gravity has the ability to pull the object back to the surface. In a sense, the object simply falls past the planet's surface.
A Mathematical Model
Calculating an objects motion is based around the Newton’s law of universal gravitation and the momentum principle with the equation [math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{object} = \vec{F}_{net} }[/math], where [math]\displaystyle{ \vec{F}_{net} }[/math] is equal to the change in the momentum of the object. The force acting on the object that has begun perpetual freefall outside the atmosphere is only gravity. The basic gravitation force equation is [math]\displaystyle{ \vec{F}_{gravity}= \lt 0,{mass}_{object}*{a}_{gravity},0\gt }[/math], where a is acceleration due to gravity: -9.8 m/s, but perpetual freefall follows Newton’s law of universal gravitation which is dependent on the mass of both objects, and their distance apart. [math]\displaystyle{ {F}_{gravity} = G \frac{m_1*m_2}{r^2}\ }[/math] where G is the universal gravitation constant: 6e-11, r is the distance between the two objects, and m1 and m2 are the masses of both objects respectively.
Because gravity is the only force acting on the object once it is free from Earth's atmosphere, [math]\displaystyle{ {Force}_{gravity} }[/math] is equal to the objects net force. Once net force is calculated, the momentum principle equation is manipulated so that the object's momentum can be updated as a function of the net force acting on the object. The equation [math]\displaystyle{ {\vec{p}_{object_{final}} } = \vec{p}_{object_{initial}}+ \vec{F}_{net}*{\Delta}{t} }[/math] is used where p is the objects momentum and [math]\displaystyle{ \Delta }[/math]t is the change in time between measurements or data points. Once change in momentum is calculated, the velocity of the object can be found using the assumption that [math]\displaystyle{ \vec{velocity}_{average} = \frac{\vec{p}_{object_{final}}}{{mass}_{object}} }[/math]. This velocity value is then used to update the objects position using [math]\displaystyle{ {\vec{r}_{object_{final}} } = \vec{r}_{object_{initial}}+ \vec{velocity}_{average}*{\Delta}{t} }[/math] where r is the object's position.
A Computational Model
Below is the computational code written in vPython language. The code consists of a setup of the scene, initial conditions and constants, calculation of force, and an update of momentum, velocity and position. All of these components are expressed visually as a simulation.
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Middling
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page