Kinematics: Difference between revisions
No edit summary |
No edit summary |
||
| Line 13: | Line 13: | ||
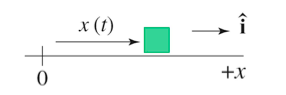
In order to construct a mathematical model of motion, it is important to understand that position can be represented as a vector quantity, having both direction and magnitude. First, let's consider an object moving in one dimension, on per se, the x-axis. The following function (on the left) models the object's position as a function of time, as depicted in the graph pictured to the right. | In order to construct a mathematical model of motion, it is important to understand that position can be represented as a vector quantity, having both direction and magnitude. First, let's consider an object moving in one dimension, on per se, the x-axis. The following function (on the left) models the object's position as a function of time, as depicted in the graph pictured to the right. | ||
[[File:onedmotion.png]] [[File:graphonedmotion.png]] | [[File:onedmotion.png]] [[File:graphonedmotion.png]] | ||
To construct a function x(t), it is important to understand change in time. Change of time is modeled by the final time observed minus the initial time, as seen in the following image. | |||
[[File:onedmotion.png]] | |||
What are the mathematical equations that allow us to model this topic. For example <math>{\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net}</math> where '''p''' is the momentum of the system and '''F''' is the net force from the surroundings. | What are the mathematical equations that allow us to model this topic. For example <math>{\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net}</math> where '''p''' is the momentum of the system and '''F''' is the net force from the surroundings. | ||
Revision as of 21:18, 5 December 2015
Claimed by Nicholas Dillard (ndillard3) Short Description of Topic
The Main Idea
The study of Kinematics is deeply rooted in modeling movement through mathematical equations and analysis. Central to the concept of movement are reference frames and coordinate system. These help answers the question, "what is the object moving relative to, and in what direction?" An example answer may be, "the car is moving relative to the ground, in the direction 20 degrees East of North."
Perhaps the most apparent components of motion are position and time. In laymen's terms, motion is a result of an objects change in position relative to a reference frame over an interval of time. Through this simple relationship, increasingly complex concepts such as velocity, acceleration, kinetic energy, and momentum can be derived. Subsequently, Kinematics lies at the center in the study of physics, and mastery of this area will spill into countless other areas.
A Mathematical Model
In order to construct a mathematical model of motion, it is important to understand that position can be represented as a vector quantity, having both direction and magnitude. First, let's consider an object moving in one dimension, on per se, the x-axis. The following function (on the left) models the object's position as a function of time, as depicted in the graph pictured to the right.
To construct a function x(t), it is important to understand change in time. Change of time is modeled by the final time observed minus the initial time, as seen in the following image.
What are the mathematical equations that allow us to model this topic. For example [math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net} }[/math] where p is the momentum of the system and F is the net force from the surroundings.
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Middling
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
References
This section contains the the references you used while writing this page