Conductors: Difference between revisions
No edit summary |
|||
| (33 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
Created by '''David Nam Spring 2025''', Edited by '''Jacob Buzzard Fall 2025''' | |||
==The Main Idea== | ==The Main Idea== | ||
A '''conductor''' is a material in which charged particles can freely move. In most conductors, such as metals, the outer (valence) electrons are loosely bound, forming what is described as a '''sea of electrons'''. These "free" electrons easily move under the influence of an external electric field or potential difference, allowing electric current to easily flow. | |||
In electrostatic equilibrium, charges within a conductor rearrange themselves so that the '''net electric field inside the conductor is zero'''. Any excess charge resides entirely on the conductor's surface, and the potential is constant throughout the interior. If a conductor is placed within an external electric field, the mobile electrons inside move almost instantaneously to reach equilibrium, setting up an induced field within the material that cancels the external one. This follows an "equal and opposite" rule, so that the induced and external electric fields cancel each other out. This induced charge movement, opposite to the net external electric field, explains important physics phenomena, such as: | |||
Electric | * Electric shielding (Faraday cages) | ||
** Because the electric field inside a conductor is zero, a closed conducting shell, called a Faraday cage, can protect its interior from the influence of external electric fields. | |||
* Induced charge seaparation on conductor surfaces | |||
** When a neutral conductor is placed in an external electric field, its free electrons shift opposite the field's direction. This creates a region of excess '''negative charge''' on one side and excess '''positive charge''' on the other. Though the conductor remains overall neutral (as charge is conserved), this '''polarization''' allows it to interact with nearby charges. | |||
* Uniform potential inside conducting objects | |||
** Since charges move freely within the conductor until equilibrium is reached, every point inside a conductor shares the same electric potential, in other words, the potential is uniform. At equilibrium, this means no current flows within the conductor, and the potential difference between any two points inside the conductor is '''zero'''. | |||
Conductors | Conductors are essential to the flow of electric current in circuits. When connected to a voltage source, like a battery, the applied potential difference drives electrons through the conductor, producing a measurable current. The ability of a material to conduct depends on its atomic structure, external temperature, and geometry. Metals such as Cu, Ag, and Al are excellent conductors due to their high density of free electrons. | ||
[[File:Cross section and length image.gif|right|180 px]] There are some factors that can change the conductance of a conductor. Shape and size, for example, affect the conductance of an object. A thicker(larger cross sectional area A in the diagram) piece will be a better conductor than a thinner piece of the same material and other dimensions | Because conductors inherently allow charge to move readily, they are used to transmit electrical energy in an efficient manner, used in real-life scenarios such as circuits and power lines. Their behavior under external electric fields forms a foundation for understanding resistance, capacitance, circuits, and electromagnetic induction. | ||
===Factors Affecting Conductance=== | |||
[[File:Cross section and length image.gif|right|180 px]] There are some factors that can change the conductance of a conductor. Shape and size, for example, affect the conductance of an object. A thicker(larger cross sectional area A as shown in the diagram) piece will be a better conductor than a thinner piece of the same material and other dimensions. This is the same concept that a thicker piece of wire allows for greater current flow. The larger cross sectional area allows for more flow of charge carriers. A shorter conductor will also conduct better since it has less resistance than a longer piece. Conductance itself can also change conductivity. In actively conducting electric current, the conductor heats up. This is secretly the third factor affecting conductance: temperature. Changes in temperature can cause the same object to have a different conductance under otherwise identical conditions. The most well known example of this is glass. Glass is more of an insulator at typical to cold temperatures, but becomes a good conductor at higher temperatures. Generally, metals are better conductors at cooler temperatures. This is because an increase in temperature is an increase in energy, specifically for electrons. | |||
[[File:Conductor chart.gif|600 px]] | |||
===A Microscopic Model=== | |||
Microscopically, conductors are made up of a lattice of '''positively charged nuclei''' surrounded by freely moving '''electrons''' throughout the material. These electrons are known as '''delocalized electrons''', meaning that they are not bound to any specific atom, instead moving randomly within the solid. | |||
[[File:Electron Sea (Plasma).jpg|300px]] | |||
When no external electric field is applied, the motion of these electrons is random, resulting in '''no net current'''. However, when an electric field is introduced, these electrons experience a force opposite the direction of the field and begin to drift slightly with a '''drift velocity'''. Although this drift velocity is small, the large amount of electrons collectively moving produces an observable '''electric current'''. | |||
There is a relationship between conductivity and temperature: as temperature increases, the amount of phonons, or what we can see as the vibration of atoms in the lattice, increases. This increased number of phonons scatters these freely moving electrons more frequently, increasing resistance, and therefore decreasing conductivity. | |||
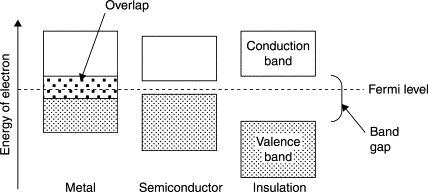
From a quantum-mechanical and materials science perspective, the behavior of conductors is governed by their energy '''band structure'''. In solids, closely spaced atomic orbitals overlap to form continuous ranges of energy that are known as bands. In '''conductors (metals)''', the '''valence band''', which contains the outer (valence) electrons and the '''conduction band''' either overlap or have a nonexistent band gap. Because of this overlap, electrons can easily move to higher-energy states and flow under even a weak electric field. | |||
By contrast, '''insulators''' have a large band gap, so electrons cannot reach the conduction band, which is why there is a net electric field inside an insulator at equilibrium and polarization occurs instead. '''Semiconductors''' have a moderate band gap, usually less than 4 eV, allowing limited conduction depending on temperature, lending their use to fascinating applications inside our devices. | |||
[[File:Band gaps.gif|500px]] | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
====Microscopic Formulation==== | |||
The total current I through a conductor of cross-sectional area A is: <math>I = nq v_d A</math>, where n = number of charge carriers (in this case, electrons), q = charge of each carrier (for electrons, q = -e, and v_d = drift velocity of the electrons | |||
====Macroscopic Formulation (Ohm's Law)==== | |||
σ is | On a larger, circuit-level scale, the current through a conductor is related to the applied voltage V and the resistance R in Ohm's Law: <math>V = IR</math>. Resistance R depends on the material and geometry of the condcutor: <math>R = \rho \frac{L}{A}</math> where ρ is the materials' innate resistivity, L is the length of the conductor, and A is the conductor's cross-sectional area. Since conductivity is the inverse of resistivity, we can write: <math>J = σE</math> can be used to model the relationship of conductivity to electric current density, where J is electric current density, σ is conductivity of the material, and E is the applied electric field. This microscopic form of Ohm's law connects the atomic behavior of electrons to a measurable current and voltage. | ||
σ is larger for better conductors like metals and saltwater. For "perfect" conductors, σ approaches infinity. In this case, E would be zero since the current density J cannot be infinity. | |||
Materials are generally divided into three categories based on σ: | Materials are generally divided into three categories based on σ: | ||
| Line 26: | Line 58: | ||
[[File:Electric conductivity equation.jpg|400 px]] | [[File:Electric conductivity equation.jpg|400 px]] | ||
===A Computational Model=== | ===A Computational Model=== | ||
[[File:Conductor computational model.PNG|right|400 px]] | |||
http://www.physics-chemistry-interactive-flash-animation.com/electricity_electromagnetism_interactive/electric_conductors_insulators.htm | [http://www.physics-chemistry-interactive-flash-animation.com/electricity_electromagnetism_interactive/electric_conductors_insulators.htm This simple interactive] is a great way to see which real objects are made of conducting or insulating material. Try to guess which objects will allow for flow of electricity before you test with the interactive. | ||
https://phet.colorado.edu/en/simulation/semiconductor | https://phet.colorado.edu/en/simulation/semiconductor | ||
| Line 40: | Line 70: | ||
===Simple=== | ===Simple=== | ||
Material A has a resistivity of <math> 5.90 \cdot 10^{-8} Ω \cdot m </math> and Material B has a conductivity of <math> 1.00 \cdot 10^7 S/m </math>. They are the same size and temperature. Which is a better conductor? | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | ||
| Line 46: | Line 76: | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
We can change Material A's resistivity to conductivity with the formula σ = 1/ρ. σ = <math>\frac{1}{(5.90 \cdot 10^{-8} Ω \cdot m)} = 1.69 \cdot 10^7 S/m</math>. Since Material A has a greater conductivity, it is a better conductor. | |||
''These numbers are the real conductivities of Zinc (Material A) and Iron (Material B).'' | |||
</div></div> | </div></div> | ||
===Middling=== | ===Middling=== | ||
A negatively charged iron block is placed in a region where there is an electric field downward (in the -y direction). What will be the charge distribution of the iron block in this field? (Problem 47 from Matter and Interactions, page 583) | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | ||
| Line 57: | Line 89: | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
[[File:Conductor question diagram.jpg|300 px]] | |||
Remember that in the direction of an electric field is traditionally the direction of positive charge movement. Since the iron block is a conductor, it has electrons that are free to move and will travel opposite the direction of the electric field. This will leave an excess of positive charge at the bottom of the block and an excess of negative charge at the top of the block, as shown in the diagram. | |||
</div></div> | </div></div> | ||
===Difficult=== | ===Difficult=== | ||
A negatively charged copper sphere (conductor!) is placed near a small positively charged rod. Describe the charge distribution on the sphere and explain the resulting forces between the rod and the sphere. | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | ||
| Line 68: | Line 102: | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
# The free electrons in the copper sphere are attracted to and move toward the positive rod, leaving a region of positive charge on the opposite side. | |||
# This '''induced charge separation''' creates a net attractive force between the sphere and the rod, similar to polarization problems. | |||
# Even though the sphere was initially neutral overall since it was a condcutor, it experiences a net force because opposite charges are closer to the rod than like charges. | |||
''Maybe put a harder problem here'' | |||
</div></div> | </div></div> | ||
==Connectedness== | ==Connectedness== | ||
===MSE (Materials Science and Engineering)=== | |||
Conductors are extremely fundamental in materials science and engineering, since the atomic structure and behavior of electrons determine electrical properties. Materials scientists study how the arrangement of atoms, charge carrier density, lattice structure, and phonons affect conductivity and resistivity. For example: | |||
* '''Metals:''' Copper, silver, and aluminum are excellent conductors because of their loosely bound valence electrons and nonexistent band gaps. | |||
* '''Alloys, Solid Solutions, and Composites:''' Engineers can change conductivity by mixing many different elements or combining materials to meet specific performance needs, like mechanical strength or corrosion resistance without losing electrical efficiency. | |||
* '''Semiconductors:''' Understanding how n- and p-doping changes charge carrier concentration is essential for designing high-tech electronic devices and sensors. | |||
By learning and mastering the concepts of conductors, MSE students and students in other engineering disciplines alike gain insight into important structure-property relationships, which is a fundamental concept in materials design and selection. This knowledge applies to a vast array of fields utilizing electricity such as electronics, power systems, energy, and nanotechnology. | |||
===Industrial Applications=== | |||
Conductors have a wide array of industrial uses, from small-scale electronics to large infrastructure: | |||
* '''Electronics and Microchips:''' Conductors are the backbone of integrated circuits and PCBs (Printed Circuit Boards). Materials that have a high conductivity increase energy efficiency, prevent overheating, and improve overall device performance, which is why this is so important to research. | |||
* '''Electrical Wiring:''' Conductors such as Cu or Al carry electricity over long distances efficiently, which is important so everyday gadgets are powered. | |||
* '''Electrostatic Shielding:''' Faraday cages, which exploit the zero internal electric field property of conductors, protect sensitive medical equipment, instruments used in the aerospace industry, and other lab experiments from external electrical disturbances. | |||
===Physics Relevance=== | |||
* '''Charge Redistribution and Polarization:''' Observing how charges within a conductor move in response to external electric fields helps understand polarization and electric potential. | |||
* '''Electromagnetic Shielding:''' Conductors play a key role in concepts like Faraday cages, transformers, and induced currents. | |||
* '''Quantum Physics:''' The behavior of free electrons, band gap theory, and drift velocity help open a small window into the world of quantum mechanics. Understanding conductors is essential for advanced quantum mechanical topics such as superconductivity, semiconductors, and nanomaterials. | |||
===Research Interests=== | |||
For MSE or broader engineering students pursuing research or industry experience, knowledge of conductors helps with a wide array of fields: | |||
* '''Nanotechnology and Electronics:''' Developing low-resistivity (high-conductivity) material bridges, called interconnects, within microchips or high-efficiency nanocircuits relies on understanding electron mobility and conductor behavior. | |||
* '''Materials Innovation:''' Developing new conductive alloys, polymers, or composites requires a fundamental connection between microscopic charge carrier behavior and macroscopic conductive properties. | |||
* '''Biomedical Devices:''' Conductive materials are essential for wearable electronics or sensitive biomedical equipment, medical electrodes, and other smart materials that respond to electrical signals. | |||
By studying conductors, students within and out of MSE can develop an appreciation for how microscopic and macroscopic properties are related, influencing real-world performance in several industries. | |||
==History== | ==History== | ||
===Ancient & Early Observations=== | |||
Around 600 BC, Thales of Miletus noted that pieces of amber, when rubbed with fur, would attract lighter objects like straw or dust. This is one of the earliest recorded observations of '''static electricity''', although the concept of "conduction" was not yet defined. | |||
Over the following centuries, scientists and researchers noticed that certain materials allowed charge to move or discharge easily, while others seemed to hold charge with little movement. This was again before the distinction of conductors and insulators was fully developed, yet an important intuition. | |||
===Electricity and Conductors=== | |||
Modern research on electricity and conductors starts in the 1700s. Many different scientists contributed to the research that led to the understanding and use of conductors. Stephan Gray was one of the first of these, first studying the idea of electricity and then conductors. In Gray's time, the general consensus was that "electric virtue" was a quality that some materials could attain and others could not. Some materials, like glass, could acquire electric virtue by friction, while others, like metal, could be given electric virtue by contact with a charged object. Gray tested this theory with many different types of material, even with a child(who did work as a conductor). | |||
Dufay began research on the same topics of charge transfer and conductance just after Gray. He lengthened the list of objects that could be given electric virtue by friction. Dufay also named the growing categories. "Electrical bodies" were what we call insulators and "non-electric bodies" were what we know as conductors. While this seems backwards from the way we think about insulators and conductors, it comes from the idea that electric virtue was intrinsic to insulators because charge could be induced on these simply by friction, while conductors can only come to have a charge by contact with a charged insulator. | |||
Only when Benjamin Franklin came around some later did the ideology and vocabulary make a big switch. Franklin suggested that electricity is not created by electrical bodies through friction, but that it is a fluid shared by all bodies and can pass between them. Franklin also caused the shift in language from non-electric bodies to conductors and electric bodies to non-conductors. | |||
===Industrial & Technological Development=== | |||
With the advent of large-scale electrical generation in the late 19th century, the need for reliable conductive materials came to the forefront of innovation. For example, copper wires began to dominate the discussion due to its superior conductivity and flexibility over iron. | |||
Insulation also developed: in the 1880s, the first insulated cables used gutta-percha, and later innovations included rubber and plastics such as PVC. The study of conductor materials also tied into materials science and quantum physics: understanding the "sea of electrons" model in metals, band theory, resistivity, and how different conditions affect conduction. | |||
===The Modern Era & Materials Science=== | |||
Today, the concept of a conductor extends beyond just metals: conductive polymers, carbon-based materials, superconductors, and nanocomposites are some of the new generation of conductive materials. Now, conductors are being applied in a multitude of industries: from aerospace to biomedical to where it all started in electricity. | |||
== See also == | == See also == | ||
===Further reading=== | ===Further reading=== | ||
To learn more about conductors: | |||
*[[Polarization of a conductor]] | |||
*[[Charged Conductor and Charged Insulator]] | |||
*[[Field of a Charged Ball]] | |||
===External links=== | ===External links=== | ||
*https://www.youtube.com/watch?v=BY8ZPobU8B0 | |||
*https://www.khanacademy.org/science/ap-physics-1/ap-electric-charge-electric-force-and-voltage/conservation-of-charge-ap/v/conductors-and-insulators | |||
*https://www.youtube.com/watch?v=PafSqL1riS4 | |||
==References== | ==References== | ||
https://en.wikipedia.org/wiki/Electrical_conductor | *https://en.wikipedia.org/wiki/Electrical_conductor | ||
*https://www.thoughtco.com/examples-of-electrical-conductors-and-insulators-608315 | |||
*https://www.rpi.edu/dept/phys/ScIT/InformationProcessing/semicond/sc_glossary/scglossary.htm | |||
*http://maxwells-equations.com/materials/conductivity.php | |||
*https://en.wikipedia.org/wiki/Ohm%27s_law | |||
*https://www.youtube.com/watch?v=BY8ZPobU8B0 | |||
*https://www.physicsclassroom.com/class/estatics/Lesson-1/Conductors-and-Insulators | |||
*http://histoires-de-sciences.over-blog.fr/2018/04/history-of-electricity.the-discovery-of-conductors-and-insulators-by-gray-dufay-and-franklin.html | |||
*Benjamin, Park. A History of Electricity (The Intellectual Rise of Electricity) from Antiquity to the Days of Benjamin Franklin. J. Wiley & Sons, 1898. Google Books, https://books.google.com/books?hl=en&lr=&id=K2dDAAAAIAAJ&oi=fnd&pg=PR1&dq=ancient egypt electricity&ots=edMffcocC0&sig=zFX9kUz2FKoPcPTCf8YVId2AjhQ#v=onepage&q&f=false. | |||
*https://www.thoughtco.com/table-of-electrical-resistivity-conductivity-608499 | |||
*https://www.physicsclassroom.com/class/estatics/lesson-1/conductors-and-insulators | |||
*https://dadaoenergy.com/blog/what-is-an-electrical-conductor | |||
*https://www.geeksforgeeks.org/physics/real-life-applications-of-conductors-and-insulators | |||
https:// | *https://histoires-de-sciences.over-blog.fr/2018/04/history-of-electricity.the-discovery-of-conductors-and-insulators-by-gray-dufay-and-franklin.html | ||
https://www. | *https://www.copper.org/education/history/60centuries/electrical/electricity.php | ||
*https://www.elandcables.com/the-cable-lab/faqs/faq-what-is-the-history-of-electrical-cables | |||
[[Category:Which Category did you place this in?]] | [[Category:Which Category did you place this in?]] | ||
Latest revision as of 21:22, 20 November 2025
Created by David Nam Spring 2025, Edited by Jacob Buzzard Fall 2025
The Main Idea
A conductor is a material in which charged particles can freely move. In most conductors, such as metals, the outer (valence) electrons are loosely bound, forming what is described as a sea of electrons. These "free" electrons easily move under the influence of an external electric field or potential difference, allowing electric current to easily flow.
In electrostatic equilibrium, charges within a conductor rearrange themselves so that the net electric field inside the conductor is zero. Any excess charge resides entirely on the conductor's surface, and the potential is constant throughout the interior. If a conductor is placed within an external electric field, the mobile electrons inside move almost instantaneously to reach equilibrium, setting up an induced field within the material that cancels the external one. This follows an "equal and opposite" rule, so that the induced and external electric fields cancel each other out. This induced charge movement, opposite to the net external electric field, explains important physics phenomena, such as:
- Electric shielding (Faraday cages)
- Because the electric field inside a conductor is zero, a closed conducting shell, called a Faraday cage, can protect its interior from the influence of external electric fields.
- Induced charge seaparation on conductor surfaces
- When a neutral conductor is placed in an external electric field, its free electrons shift opposite the field's direction. This creates a region of excess negative charge on one side and excess positive charge on the other. Though the conductor remains overall neutral (as charge is conserved), this polarization allows it to interact with nearby charges.
- Uniform potential inside conducting objects
- Since charges move freely within the conductor until equilibrium is reached, every point inside a conductor shares the same electric potential, in other words, the potential is uniform. At equilibrium, this means no current flows within the conductor, and the potential difference between any two points inside the conductor is zero.
Conductors are essential to the flow of electric current in circuits. When connected to a voltage source, like a battery, the applied potential difference drives electrons through the conductor, producing a measurable current. The ability of a material to conduct depends on its atomic structure, external temperature, and geometry. Metals such as Cu, Ag, and Al are excellent conductors due to their high density of free electrons.
Because conductors inherently allow charge to move readily, they are used to transmit electrical energy in an efficient manner, used in real-life scenarios such as circuits and power lines. Their behavior under external electric fields forms a foundation for understanding resistance, capacitance, circuits, and electromagnetic induction.
Factors Affecting Conductance
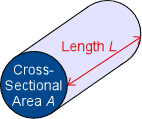
There are some factors that can change the conductance of a conductor. Shape and size, for example, affect the conductance of an object. A thicker(larger cross sectional area A as shown in the diagram) piece will be a better conductor than a thinner piece of the same material and other dimensions. This is the same concept that a thicker piece of wire allows for greater current flow. The larger cross sectional area allows for more flow of charge carriers. A shorter conductor will also conduct better since it has less resistance than a longer piece. Conductance itself can also change conductivity. In actively conducting electric current, the conductor heats up. This is secretly the third factor affecting conductance: temperature. Changes in temperature can cause the same object to have a different conductance under otherwise identical conditions. The most well known example of this is glass. Glass is more of an insulator at typical to cold temperatures, but becomes a good conductor at higher temperatures. Generally, metals are better conductors at cooler temperatures. This is because an increase in temperature is an increase in energy, specifically for electrons.
A Microscopic Model
Microscopically, conductors are made up of a lattice of positively charged nuclei surrounded by freely moving electrons throughout the material. These electrons are known as delocalized electrons, meaning that they are not bound to any specific atom, instead moving randomly within the solid.
When no external electric field is applied, the motion of these electrons is random, resulting in no net current. However, when an electric field is introduced, these electrons experience a force opposite the direction of the field and begin to drift slightly with a drift velocity. Although this drift velocity is small, the large amount of electrons collectively moving produces an observable electric current.
There is a relationship between conductivity and temperature: as temperature increases, the amount of phonons, or what we can see as the vibration of atoms in the lattice, increases. This increased number of phonons scatters these freely moving electrons more frequently, increasing resistance, and therefore decreasing conductivity.
From a quantum-mechanical and materials science perspective, the behavior of conductors is governed by their energy band structure. In solids, closely spaced atomic orbitals overlap to form continuous ranges of energy that are known as bands. In conductors (metals), the valence band, which contains the outer (valence) electrons and the conduction band either overlap or have a nonexistent band gap. Because of this overlap, electrons can easily move to higher-energy states and flow under even a weak electric field.
By contrast, insulators have a large band gap, so electrons cannot reach the conduction band, which is why there is a net electric field inside an insulator at equilibrium and polarization occurs instead. Semiconductors have a moderate band gap, usually less than 4 eV, allowing limited conduction depending on temperature, lending their use to fascinating applications inside our devices.
A Mathematical Model
Microscopic Formulation
The total current I through a conductor of cross-sectional area A is: [math]\displaystyle{ I = nq v_d A }[/math], where n = number of charge carriers (in this case, electrons), q = charge of each carrier (for electrons, q = -e, and v_d = drift velocity of the electrons
Macroscopic Formulation (Ohm's Law)
On a larger, circuit-level scale, the current through a conductor is related to the applied voltage V and the resistance R in Ohm's Law: [math]\displaystyle{ V = IR }[/math]. Resistance R depends on the material and geometry of the condcutor: [math]\displaystyle{ R = \rho \frac{L}{A} }[/math] where ρ is the materials' innate resistivity, L is the length of the conductor, and A is the conductor's cross-sectional area. Since conductivity is the inverse of resistivity, we can write: [math]\displaystyle{ J = σE }[/math] can be used to model the relationship of conductivity to electric current density, where J is electric current density, σ is conductivity of the material, and E is the applied electric field. This microscopic form of Ohm's law connects the atomic behavior of electrons to a measurable current and voltage.
σ is larger for better conductors like metals and saltwater. For "perfect" conductors, σ approaches infinity. In this case, E would be zero since the current density J cannot be infinity.
Materials are generally divided into three categories based on σ:
- Lossless Materials: σ = 0
- Lossy Materials: σ > 0
- Conductors: σ >> 0
Below is a breakdown of how conductivity is calculated. This could be considered a formula for conductivity, but it would be more accurate to think of it as a definition.
A Computational Model

This simple interactive is a great way to see which real objects are made of conducting or insulating material. Try to guess which objects will allow for flow of electricity before you test with the interactive.
https://phet.colorado.edu/en/simulation/semiconductor
Examples
Simple
Material A has a resistivity of [math]\displaystyle{ 5.90 \cdot 10^{-8} Ω \cdot m }[/math] and Material B has a conductivity of [math]\displaystyle{ 1.00 \cdot 10^7 S/m }[/math]. They are the same size and temperature. Which is a better conductor?
We can change Material A's resistivity to conductivity with the formula σ = 1/ρ. σ = [math]\displaystyle{ \frac{1}{(5.90 \cdot 10^{-8} Ω \cdot m)} = 1.69 \cdot 10^7 S/m }[/math]. Since Material A has a greater conductivity, it is a better conductor.
These numbers are the real conductivities of Zinc (Material A) and Iron (Material B).
Middling
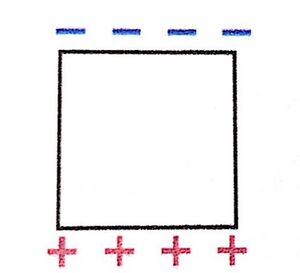
A negatively charged iron block is placed in a region where there is an electric field downward (in the -y direction). What will be the charge distribution of the iron block in this field? (Problem 47 from Matter and Interactions, page 583)
Remember that in the direction of an electric field is traditionally the direction of positive charge movement. Since the iron block is a conductor, it has electrons that are free to move and will travel opposite the direction of the electric field. This will leave an excess of positive charge at the bottom of the block and an excess of negative charge at the top of the block, as shown in the diagram.
Difficult
A negatively charged copper sphere (conductor!) is placed near a small positively charged rod. Describe the charge distribution on the sphere and explain the resulting forces between the rod and the sphere.
- The free electrons in the copper sphere are attracted to and move toward the positive rod, leaving a region of positive charge on the opposite side.
- This induced charge separation creates a net attractive force between the sphere and the rod, similar to polarization problems.
- Even though the sphere was initially neutral overall since it was a condcutor, it experiences a net force because opposite charges are closer to the rod than like charges.
Maybe put a harder problem here
Connectedness
MSE (Materials Science and Engineering)
Conductors are extremely fundamental in materials science and engineering, since the atomic structure and behavior of electrons determine electrical properties. Materials scientists study how the arrangement of atoms, charge carrier density, lattice structure, and phonons affect conductivity and resistivity. For example:
- Metals: Copper, silver, and aluminum are excellent conductors because of their loosely bound valence electrons and nonexistent band gaps.
- Alloys, Solid Solutions, and Composites: Engineers can change conductivity by mixing many different elements or combining materials to meet specific performance needs, like mechanical strength or corrosion resistance without losing electrical efficiency.
- Semiconductors: Understanding how n- and p-doping changes charge carrier concentration is essential for designing high-tech electronic devices and sensors.
By learning and mastering the concepts of conductors, MSE students and students in other engineering disciplines alike gain insight into important structure-property relationships, which is a fundamental concept in materials design and selection. This knowledge applies to a vast array of fields utilizing electricity such as electronics, power systems, energy, and nanotechnology.
Industrial Applications
Conductors have a wide array of industrial uses, from small-scale electronics to large infrastructure:
- Electronics and Microchips: Conductors are the backbone of integrated circuits and PCBs (Printed Circuit Boards). Materials that have a high conductivity increase energy efficiency, prevent overheating, and improve overall device performance, which is why this is so important to research.
- Electrical Wiring: Conductors such as Cu or Al carry electricity over long distances efficiently, which is important so everyday gadgets are powered.
- Electrostatic Shielding: Faraday cages, which exploit the zero internal electric field property of conductors, protect sensitive medical equipment, instruments used in the aerospace industry, and other lab experiments from external electrical disturbances.
Physics Relevance
- Charge Redistribution and Polarization: Observing how charges within a conductor move in response to external electric fields helps understand polarization and electric potential.
- Electromagnetic Shielding: Conductors play a key role in concepts like Faraday cages, transformers, and induced currents.
- Quantum Physics: The behavior of free electrons, band gap theory, and drift velocity help open a small window into the world of quantum mechanics. Understanding conductors is essential for advanced quantum mechanical topics such as superconductivity, semiconductors, and nanomaterials.
Research Interests
For MSE or broader engineering students pursuing research or industry experience, knowledge of conductors helps with a wide array of fields:
- Nanotechnology and Electronics: Developing low-resistivity (high-conductivity) material bridges, called interconnects, within microchips or high-efficiency nanocircuits relies on understanding electron mobility and conductor behavior.
- Materials Innovation: Developing new conductive alloys, polymers, or composites requires a fundamental connection between microscopic charge carrier behavior and macroscopic conductive properties.
- Biomedical Devices: Conductive materials are essential for wearable electronics or sensitive biomedical equipment, medical electrodes, and other smart materials that respond to electrical signals.
By studying conductors, students within and out of MSE can develop an appreciation for how microscopic and macroscopic properties are related, influencing real-world performance in several industries.
History
Ancient & Early Observations
Around 600 BC, Thales of Miletus noted that pieces of amber, when rubbed with fur, would attract lighter objects like straw or dust. This is one of the earliest recorded observations of static electricity, although the concept of "conduction" was not yet defined.
Over the following centuries, scientists and researchers noticed that certain materials allowed charge to move or discharge easily, while others seemed to hold charge with little movement. This was again before the distinction of conductors and insulators was fully developed, yet an important intuition.
Electricity and Conductors
Modern research on electricity and conductors starts in the 1700s. Many different scientists contributed to the research that led to the understanding and use of conductors. Stephan Gray was one of the first of these, first studying the idea of electricity and then conductors. In Gray's time, the general consensus was that "electric virtue" was a quality that some materials could attain and others could not. Some materials, like glass, could acquire electric virtue by friction, while others, like metal, could be given electric virtue by contact with a charged object. Gray tested this theory with many different types of material, even with a child(who did work as a conductor).
Dufay began research on the same topics of charge transfer and conductance just after Gray. He lengthened the list of objects that could be given electric virtue by friction. Dufay also named the growing categories. "Electrical bodies" were what we call insulators and "non-electric bodies" were what we know as conductors. While this seems backwards from the way we think about insulators and conductors, it comes from the idea that electric virtue was intrinsic to insulators because charge could be induced on these simply by friction, while conductors can only come to have a charge by contact with a charged insulator.
Only when Benjamin Franklin came around some later did the ideology and vocabulary make a big switch. Franklin suggested that electricity is not created by electrical bodies through friction, but that it is a fluid shared by all bodies and can pass between them. Franklin also caused the shift in language from non-electric bodies to conductors and electric bodies to non-conductors.
Industrial & Technological Development
With the advent of large-scale electrical generation in the late 19th century, the need for reliable conductive materials came to the forefront of innovation. For example, copper wires began to dominate the discussion due to its superior conductivity and flexibility over iron.
Insulation also developed: in the 1880s, the first insulated cables used gutta-percha, and later innovations included rubber and plastics such as PVC. The study of conductor materials also tied into materials science and quantum physics: understanding the "sea of electrons" model in metals, band theory, resistivity, and how different conditions affect conduction.
The Modern Era & Materials Science
Today, the concept of a conductor extends beyond just metals: conductive polymers, carbon-based materials, superconductors, and nanocomposites are some of the new generation of conductive materials. Now, conductors are being applied in a multitude of industries: from aerospace to biomedical to where it all started in electricity.
See also
Further reading
To learn more about conductors:
External links
- https://www.youtube.com/watch?v=BY8ZPobU8B0
- https://www.khanacademy.org/science/ap-physics-1/ap-electric-charge-electric-force-and-voltage/conservation-of-charge-ap/v/conductors-and-insulators
- https://www.youtube.com/watch?v=PafSqL1riS4
References
- Benjamin, Park. A History of Electricity (The Intellectual Rise of Electricity) from Antiquity to the Days of Benjamin Franklin. J. Wiley & Sons, 1898. Google Books, https://books.google.com/books?hl=en&lr=&id=K2dDAAAAIAAJ&oi=fnd&pg=PR1&dq=ancient egypt electricity&ots=edMffcocC0&sig=zFX9kUz2FKoPcPTCf8YVId2AjhQ#v=onepage&q&f=false.