Polarization of a conductor
Edited by Kevin Kim Fall 2025
Claimed by Kevin Kim Fall 2025
The Main Idea
A conductor contains mobile charged particles that move freely through a material. Based on the definition of a conductor, it is easily assumed that stronger conductors can have charged particles moving more freely and over larger distances. There are two main situations where this can be observed in: ionic solutions and metals. Conductors contain valence electrons that can fully migrate from atom to atom rather than being bound to a single atom. Therefore, unlike insulators, the electric field inside a conductor remains zero at all times, even with an external electric field acting on it.
Ionic Solutions
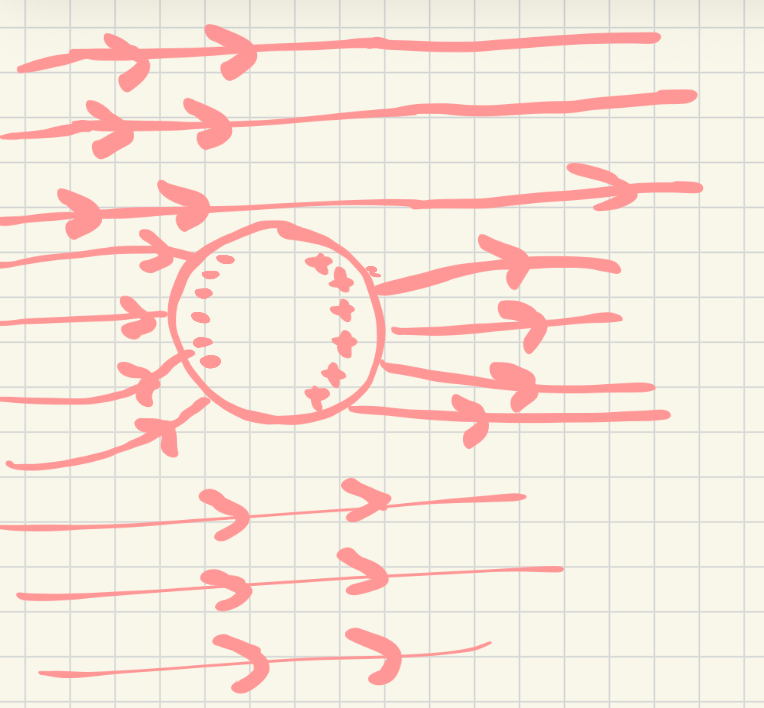
Ionic solutions, such as KCl or NaCl or NaI (solutions in which the ions dissociate), have individual ions of the dissociated particles. For example, a solution of NaI will have Na+, I-, and because it is an aqueous salt solution, some H+ and OH- as well. When an electric field is applied to this solution, the particles move in the direction of the force applied by the electric field. However, the charged particles move in a direction and accumulate, therefore creating a charge gradient, which in turn creates its own electric field! This can be shown in Figure 1, taken from the textbook. The net electric field in the region is the superposition of the applied (external) field and the electric field created by the relocation of charges in the material. While ions are constantly moving, this is an accurate snapshot of what would be expected in the event of applied field/force. Furthermore, while ions are constantly moving in the solution, there is a measurable excess of ions on the edges that generates the field.
(Matter and Interactions)
While polarization is a rapid process once initiated, it is not an on-off binary process. The instant that an electric field is applied, the drift speed is nonzero and the particles start tending towards the direction of the electric field. As ions pile up on the sides of the solution, the net electric field inside becomes weaker and the system approaches an equilibrium at a microscopic level. At this equilibrium, drift speed is 0 and there is no NET MOTION of mobile charges in solution.
Electric Field Inside A Conductor
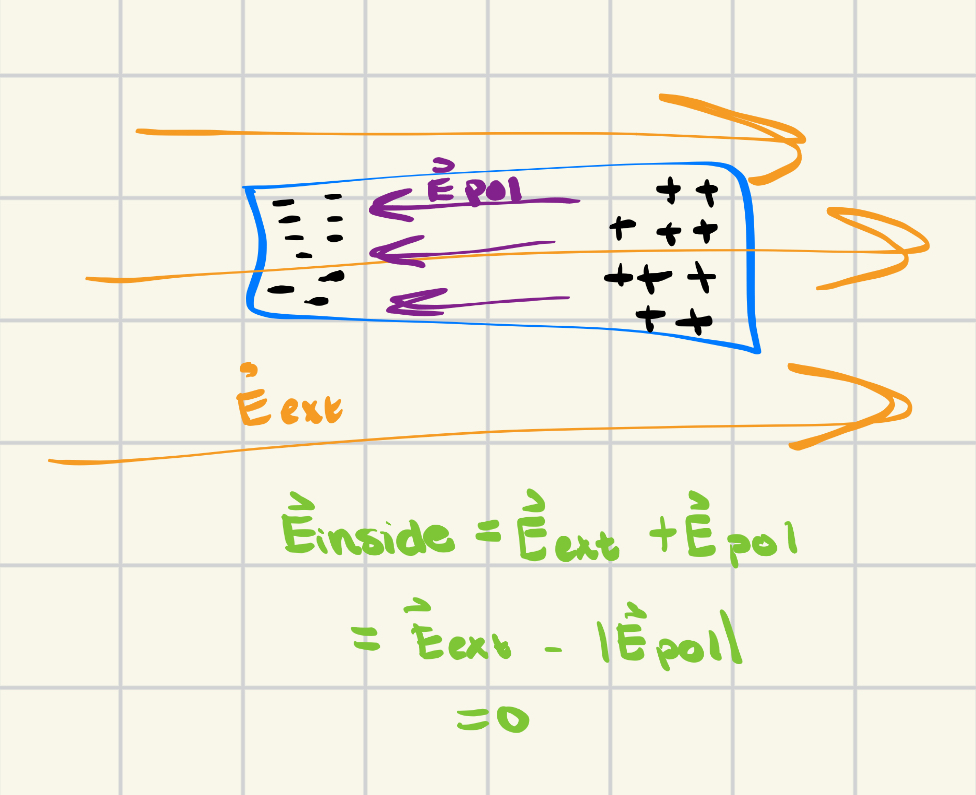
Due to the superpower of conductors being able to move its valence electrons from atom to atom, an external field causes the conductor to polarize so that one there are an uneven distribution of charges on both sides. Referring to the image above, the electrons configure themselves into the left side of the conductor, where the electric field is approaching, to create a net negative on the left and a net positive on the right, which is caused by the lack of electrons on the right side of the conductor. If the net electric field were to be approaching from the right, then the electrons would have reconfigured into the right side of the conductor, leaving a net positive on the left side still and becoming polarized yet again.
A very important fact to remember about the polarization of conductors is that the electric field inside will always be equal to zero. This is because when the conductor is polarized, the surface charges rearrange themselves as stated before where the electrons move towards the approaching electric field. Due to this, and the idea that electric fields emerge from protons and move into the direction of electrons, the surface charges themselves create an electric field in the opposite direction of the external electric field. This electric field caused by the surface charges (Epol) are of the same magnitude of the external electric field, and because they are moving in opposite directions, the overall net electric field inside the conductor ultimately comes out to zero.
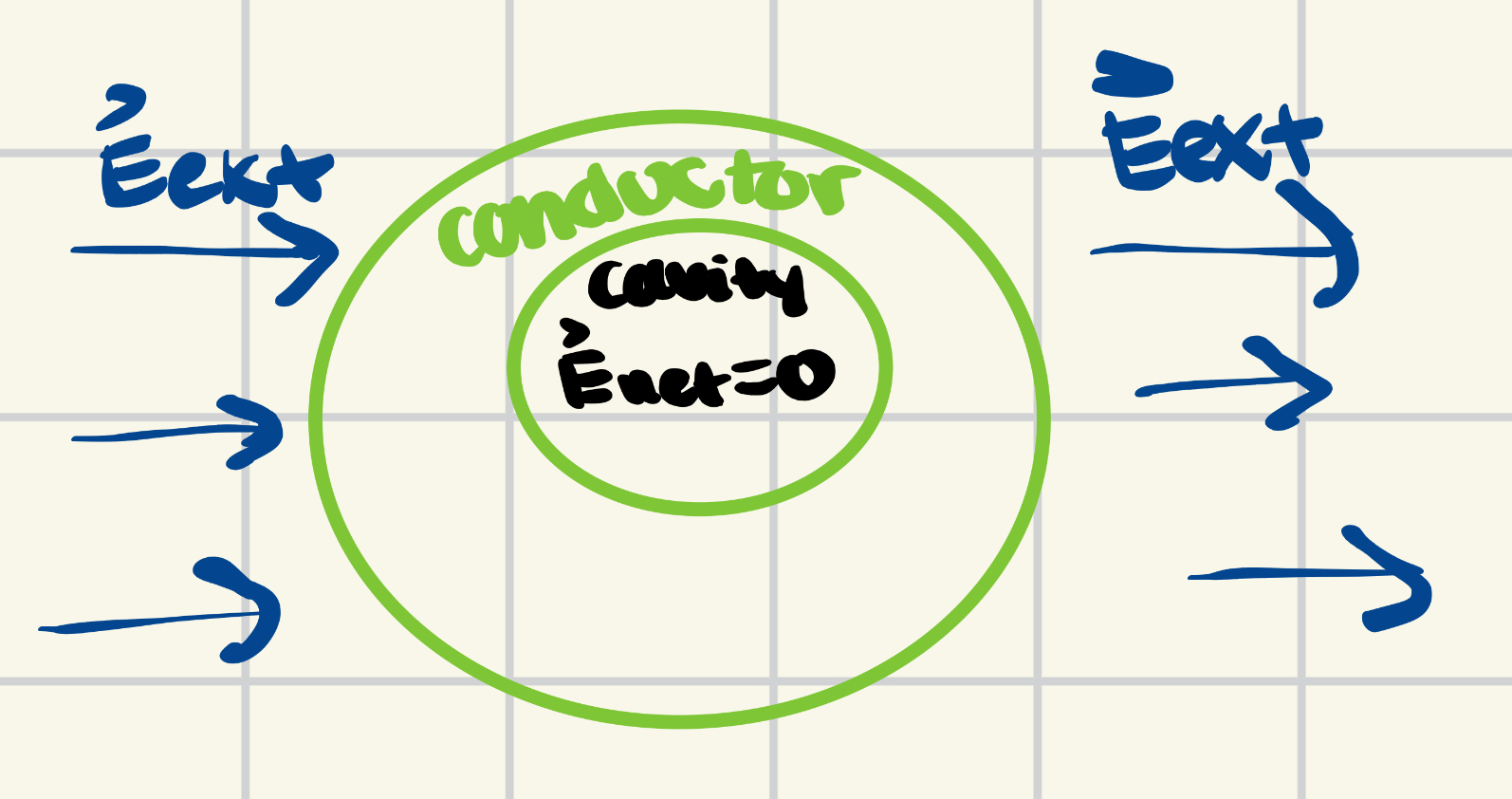
Now that we covered what happens to a solid conductor, the question arises to what happens if there is a cavity inside of a conductor. To figure out a result, we first need to assume that the cavity inside the conductor completely empty. When an external electric field affects a conductor with a cavity, the electric field inside the conductor as well as the cavity will sum out to zero yet again.
Metals
Metals are an interesting idea structurally. Atoms of a metal are arranged in a rigid, ordered structure, sometimes known as a lattice structure (similar to crystal). This structure causes an interesting pattern of behavior. The inner electrons of each of these ordered atoms are attracted to the positively charged nucleus. Some of the outer electrons engage in solid atom interactions (Ball and Spring Model), but other outer electrons participate in a pool of electrons that is allowed to move freely across the solid, in an "electron sea". While they can move across the solid, they are very hard to extract and there are obviously some limitations to its direction of movement (different from liquid ionic solutions), but the mobile electron sea makes metals great conductor candidates (and thus are used in so many practical applications; including wires, microchips, cars, etc.)
There is a caveat to this, however. You may ask, won't the electrons repel each other and not allow for this kind of movement? Yes, but the presence of the positive cores neutralizes this interaction. There is, therefore, no net interaction between the electrons inside a metal. Thus, the sea of electrons moves independent of effects from electrons and positive cores and appear not to interact with each other. The model of electron motion is defined by the Drude model; the steps of which are shown here:
1) When an electric field is applied in a metal, the electrons get excited and accelerate.
2) The electrons lose their energy when they collide with the lattices of the positive atomic cores.
3) After the collision, the electrons again get accelerated and the entire process repeats itself.
(Matter and Interactions)
This YouTube video does an excellent job of explaining the concept in further detail:
https://www.youtube.com/watch?v=HKgOpmX-OFI
A Mathematical Model
In the phenomenon of drift speed in ionic solutions, the Na+ and I- ions will move and bounce around a good bit when the external field is applied, but due to collisions, they do not maintain a specific speed or trajectory. This is in spite of whether or not the force experienced is constant. In order to keep the ions moving at constant speed, also known as the drift speed, a constant electric field must be applied. This is modeled mathematically using the following equation:
- [math]\displaystyle{ \bar{v}={u}{E_{net}} }[/math]
where [math]\displaystyle{ \bar{v} }[/math] is the drift speed, [math]\displaystyle{ u }[/math] is the mobility of the charge [math]\displaystyle{ {\frac{(m/s)}{(N/C)}} }[/math], and [math]\displaystyle{ E_{net} }[/math] is the net electric field applied to the ionic solution. The proportionality constant, [math]\displaystyle{ u }[/math], is determined for the ions based on the solution and will be usually given or easy to derive in all practical problem sets using this concept. This is a linear relationship overall, meaning that the charge will stop moving in the event of no electric field.
The average speed for electrons in a metal is defined by [math]\displaystyle{ \bar{v} }[/math]; the drift speed, as mentioned earlier. For metals this equation is:
- [math]\displaystyle{ \bar{v}={\frac{{e}{E_{net}}{Δt}}{m_{e}}} }[/math]
where [math]\displaystyle{ \bar{v} }[/math] is the drift speed, [math]\displaystyle{ e }[/math] is the charge of the electron, [math]\displaystyle{ {E_{net}} }[/math] is the net applied electric field, [math]\displaystyle{ {Δt} }[/math] is the average time between collisions, and [math]\displaystyle{ {m_{e}} }[/math] is the mass of the electron. The average time between collisions is used because the time between each collision is uncontrollable and inconsistent. This equation is derived from the momentum equation where [math]\displaystyle{ {Δp} = {F_{net}}{Δt} }[/math] and [math]\displaystyle{ {F} = {e}{E_{net}} }[/math].
A Computational Model
This website has a great interactive for the polarization of a metal. Notice that the positive charges in the can do not move while the negative charges are repelled and attracted by the other objects.
Examples
Simple
The mobility of electrons in copper is [math]\displaystyle{ {0.0045}{\frac{(m/s)}{(N/C)}} }[/math]. How much net electric field would be needed in order to give the electrons in copper a drift speed of [math]\displaystyle{ {0.0015}{\frac{m}{s}} }[/math]?
This is a simple problem using the formula given for drift speed
- [math]\displaystyle{ \bar{v}={u}{E_{net}} }[/math]
Thus, [math]\displaystyle{ {E_{net}} = {\frac{\bar{v}}{u}} }[/math] = [math]\displaystyle{ \frac{0.0015}{0.0045} }[/math] = [math]\displaystyle{ {0.333}{\frac{N}{C}} }[/math].
This also makes sense from a units perspective, as our solution is in [math]\displaystyle{ \frac{N}{C} }[/math], the speed is [math]\displaystyle{ \frac{m}{s} }[/math], and the mobility is given in [math]\displaystyle{ \frac{(m/s)}{(N/C)} }[/math].
Middling
In a simple metal lattice structure, an electric field of [math]\displaystyle{ {10}{\frac{N}{C}} }[/math] is applied and 15 collisions are observed. The time between collisions increases by one second after each collision, starting with 1 second, from collision 1 to collision 2. After 15 collisions, what is the drift speed of an electron in this metal lattice structure?
This is a slightly more complex problem that requires a bit of analytical thinking and application of a formula. The formula:
- [math]\displaystyle{ \bar{v}={\frac{{e}{E_{net}}{Δt}}{m_{e}}} }[/math]
All of the quantities are known. [math]\displaystyle{ {e} = {1.6}{*}{10^{-19}}{C} }[/math], [math]\displaystyle{ {E_{net}} = {10}{\frac{N}{C}} }[/math], [math]\displaystyle{ {m_{e}} = {9.1}{*}{10^{-31}} }[/math].
However, [math]\displaystyle{ {Δt} }[/math] is not immediately discernible. The question asks for the drift speed after 15 collisions. It might be some people's thought to just use the time between the 14th and 15th collision as the [math]\displaystyle{ {Δt} }[/math] in the equation. [math]\displaystyle{ {Δt} }[/math] refers to the AVERAGE time between collisions. Therefore, you can calculate it by summing the collision times for all 15 collisions(1 + 2 + 3... + 15) and dividing by the number of collisions. In this case, the [math]\displaystyle{ {Δt} }[/math] would therefore be 8 seconds.
Plugging these numbers in, you get: [math]\displaystyle{ {1.2}{*}{10^{15}}{\frac{m}{s}} }[/math]. This is extremely fast. As you can see, this speaks to how quickly electrons move through substances and how quickly polarization occurs, both in metals and in ionic solutions.
Difficult
Summarize the difference between conductors and insulators in the following 4 categories:
1) Mobile Charges
2) Polarization
3) Equilibrium
4) Excess Charge
1) Conductors have mobile charges while insulators do not.
2) The sea or mass of mobile electrons moves when an electric field is applied to a conductor. When an electric field is applied to an insulator, individual atoms polarize.
3) The net electric field is 0 in a conductor at equilibrium, whereas there is a nonzero electric field in an insulator at equilibrium.
4) Excess charge spreads over the surface of a conductor, but clumps in patches in an insulator.
(Matter and Interactions)
Connectedness
This is a very important concept in polarization. As mentioned earlier, when a conductor is polarized, the electron sea moves rapidly and cause polarization. When an insulator has an applied electric field, the individual atoms or molecules become polarized. An interesting aspect of this is the concept of dielectric. A dielectric is a material or substance that is usually an insulator, but when an electric field is applied, the electrons shift slightly from their usual equilibrium creating a positive and negative space and thus, polarization. Usually, a dielectric is a material with extremely high polarizability, which is extremely useful in the real world. The concept was developed by William Wheewell during a discussion with Michael Faraday. Dielectrics are commonly used in developing capacitors.
History
[a student should fill this out]
See also
External links
Youtube video for polarization in conductors
Youtube video for a realize life example
Further Reading
References
Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2015. Print.