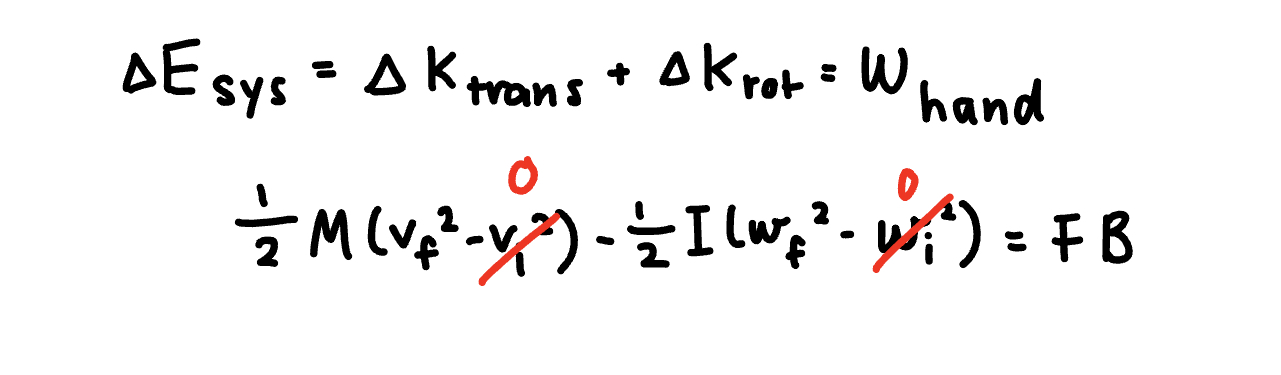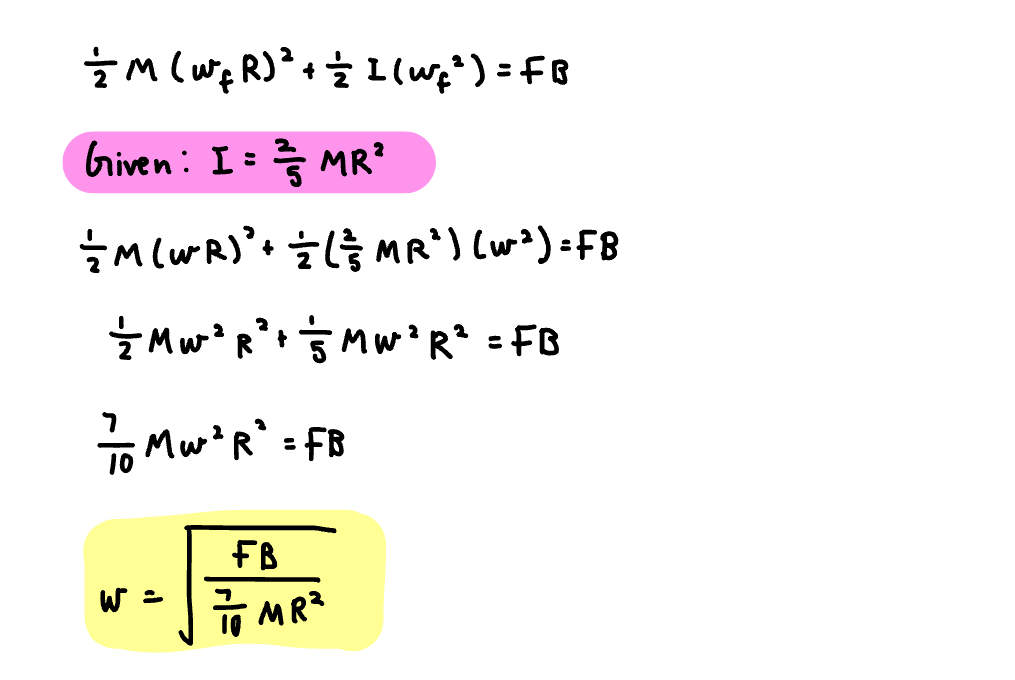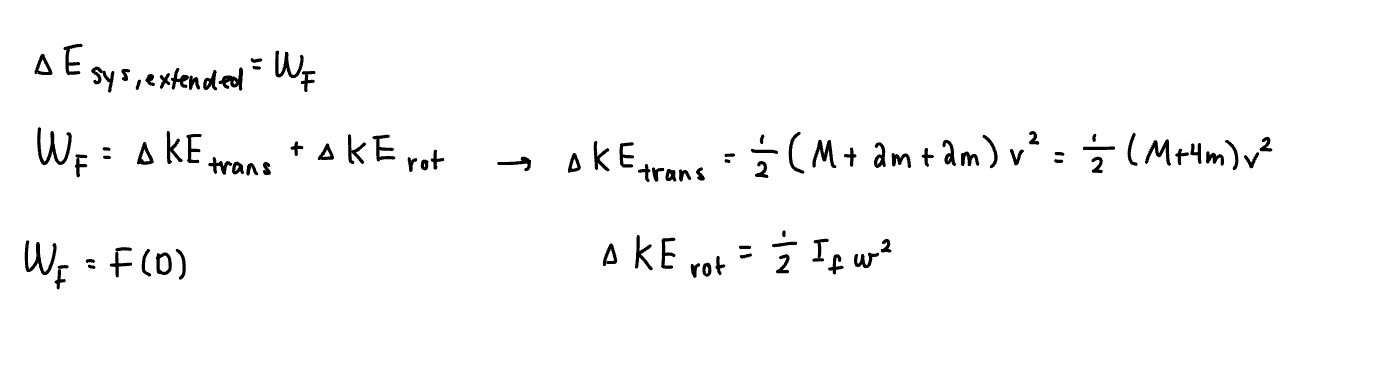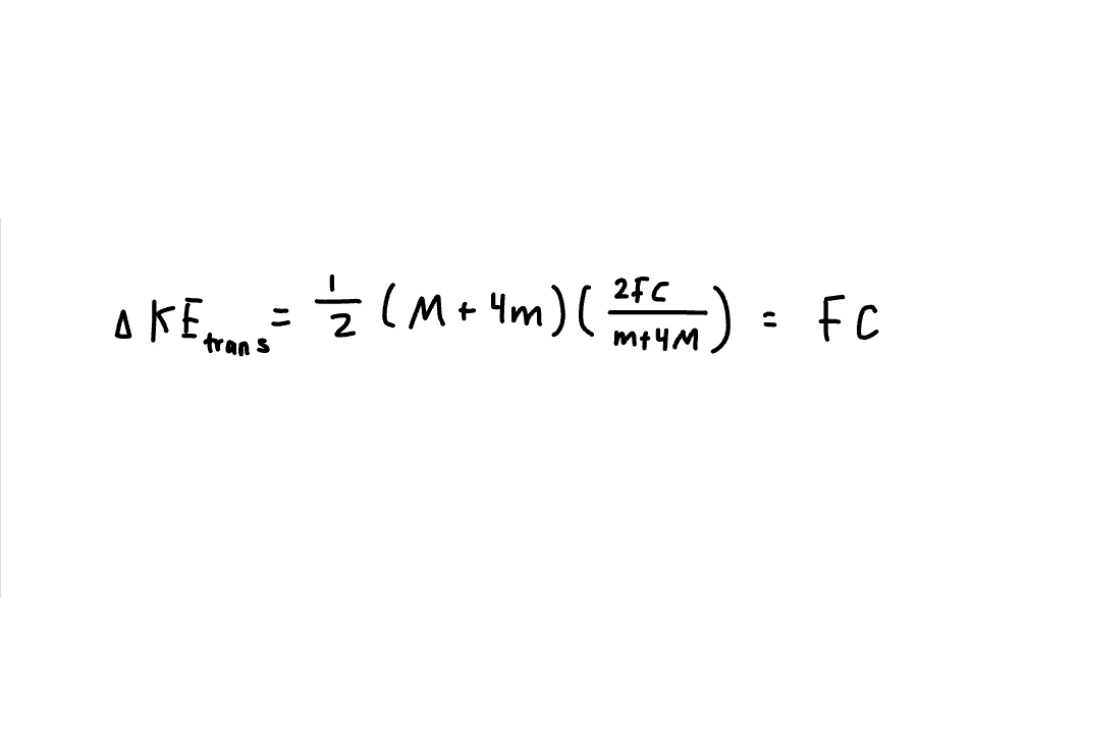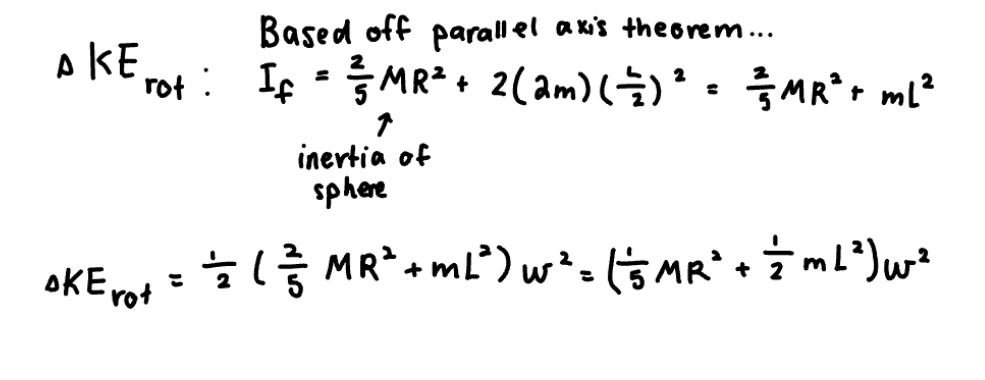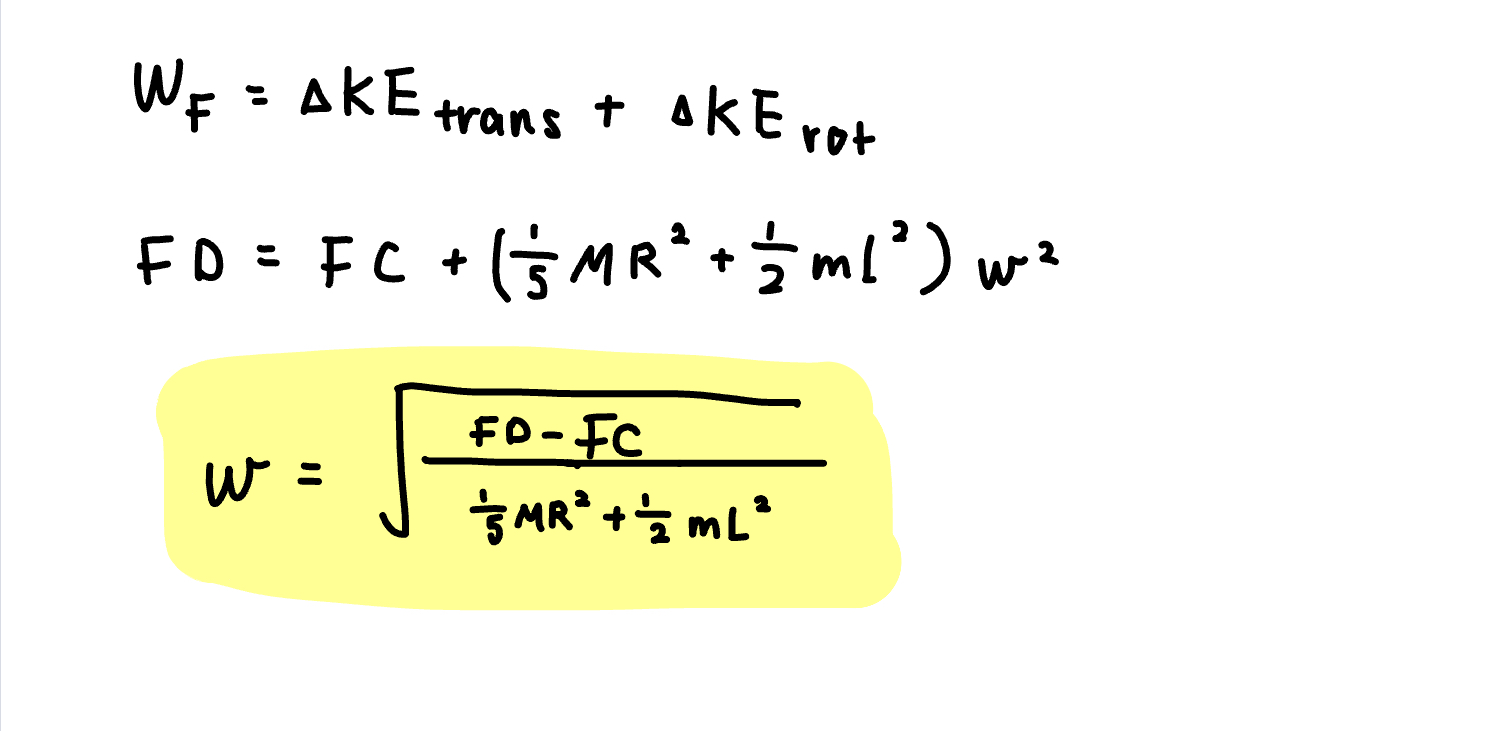Work and Energy for an Extended System
ATHENA WU Spring23
The Main Idea
Unlike the point particle system where the only energy possible is translational kinetic energy, an extended object can rotate, vibrate, and change shape. Though the point particle system and the extended system both have the same total mass, and are both acted on by the same net force, the point particle system, has no rotational motion, vibrational motion, or internal energy because all of the forces act at the location of the point particle. In contrast, forces act at different locations on the mass in an extended system, thus causing them to rotate, vibrate and stretch. Because of these qualities, not every part of the system always moves in the same direction as the center of mass moves.
When calculating work done on an extended system, the displacement of every point where a force is applied must be considered separately, because it matters where each force is applied.
A Mathematical Model
Work and Energy for an Extended System:
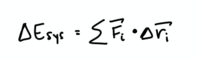
This equation assumes that each force is constant during the displacement. If each force is not constant during the displacement, the work of each force as an integral of [math]\displaystyle{ \vec{F}_{i}•d\vec{r}_{i} }[/math] must be calculated either analytically or numerically.
A Computational Model
A Jumping Kangaroo Modeled as an Extended Object:
If one were to model a jumping kangaroo as a point particle system, the change in translational kinetic energy could be derived. However in the real world, Kangaroos are not a point particle, but rather an extended system where energy changes occur in the legs and arms of the kangaroo relative to the center of mass. Chemical energy and thermal energy are just two more examples of energy changes that may occur in extended systems but not in point particle systems.
The work done on a point particle system is not the same as the work done on an extended system. Because forces are applied in many different locations on the mass in an extended system, sometimes these forces act through different distances than the displacement of the center of mass of the system, for different sections of the system move different distances. The following free-body diagram a modeled extended system illustrates how these individual forces may act at different locations:
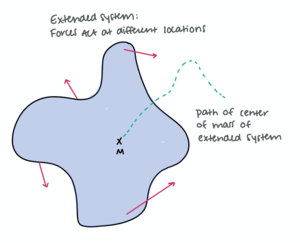
Note: Figure created by author
When considering all the possible changes in energy when a Kangaroo jumps, the energy equation for the Kangaroo modeled as an extended system (ignoring Q, or the transfer of energy due to a temperature difference between the Kangaroo and the surrounding air), should look like the following equation:

Note: Figure created by author
The change in relative kinetic energy and the change in internal energy do not appear in the energy equation for the point particle system because the point particle system only focuses on the translational motion of the center of mass point. The change in relative kinetic energy includes the rotation of the legs and the swinging of the upper body and tail of the Kangaroo. The change in internal energy includes the increase in thermal energy of the Kangaroo's body and the decrease in chemical energy that was previously chemically stored in the Kangaroo's body. This computational model of the jumping Kangaroo allows one to visualize how unlike the point particle system, the extended system changes shape due to the bending of the legs, arms, and torso of the Kangaroo during the jump.
Example
Simple
Solution
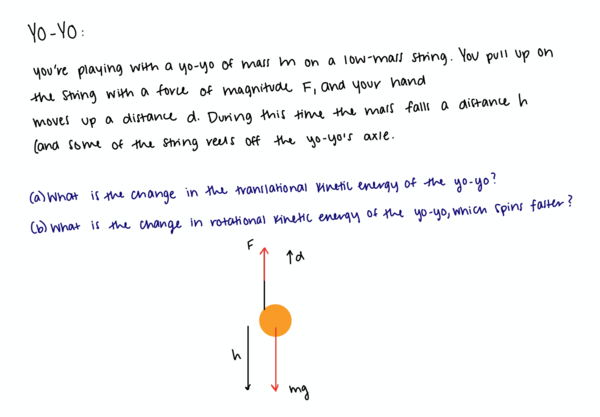
(a)
System: Point Particle
Surroundings: Hand and Earth
Initial State: Point particle with initial translational kinetic energy
Final State: Point particle with final translational kinetic energy
Energy Principle (keep in mind that point particle systems only have translational kinetic energy!)
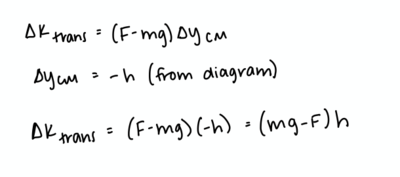
Solution
(b)
Middling
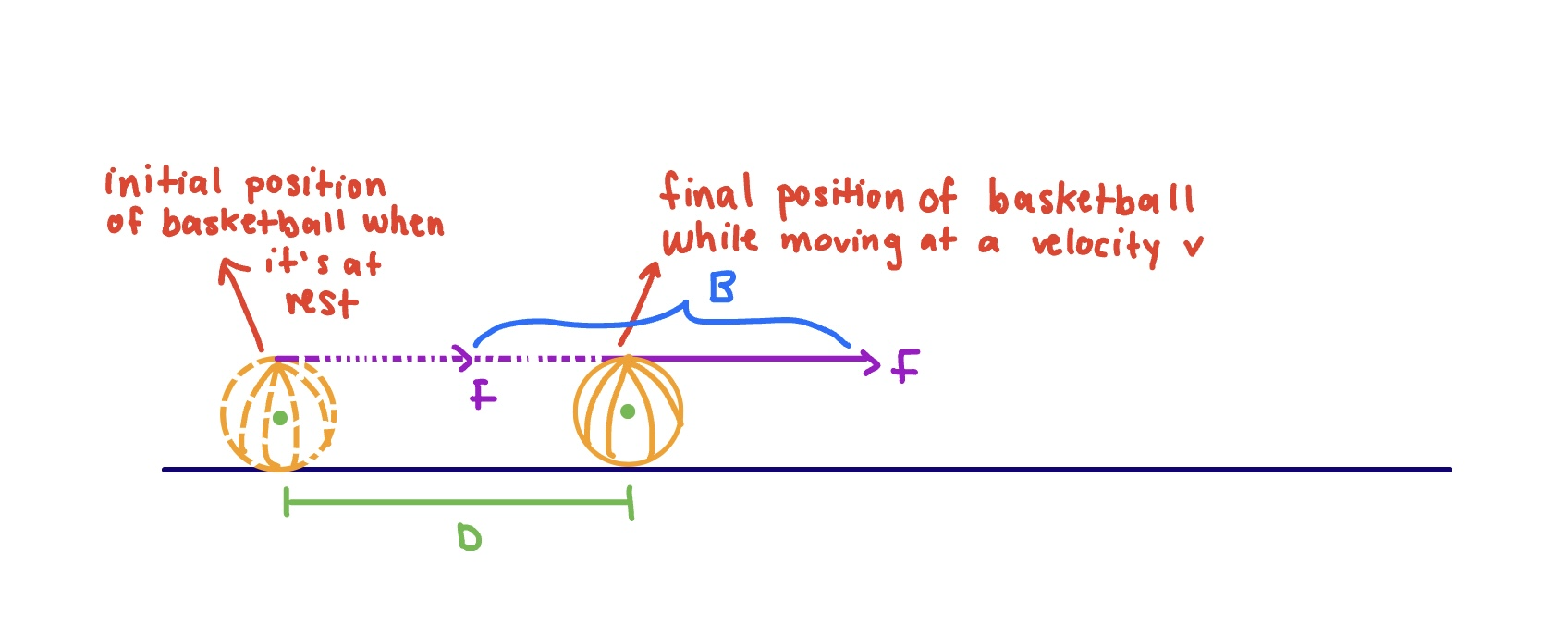
Suppose that there is a basketball with mass M and radius R on a frictionless surface with an inertia of I = 0.4M(R^2). The ball is originally at rest; a hand then pulls the string that's around the ball with constant force F so that the ball rolls without slipping. The center of mass for the yo-yo moves a distance of D and the hand moves a total distance of B (while exerting force F throughout such distance). Find the angular speed ω at the time where the center of mass of the yo-yo is distance D away from its starting point.
Solution
First off, we know that the real system we are dealing with is the basketball, with our surroundings being the hand that is exerting force F and the frictionless surface.
We also know that the change in energy of our real system is equal to the sum of the change in translational kinetic energy and the change in rotational kinetic energy. This should also be equal to the work of the hand on the basketball. However, a place that is tricky is that the work of the hand is FB. After all, the force that the hand exerts on the basketball is F and the hand moves a total distance of B. When we are dealing with real and extended systems, even though the center of mass moved a distance of D, we want to take into account the distance that the force moved, which is B in our case.
However, what is velocity v? Well, we know that v = ωR, as the basketball is rolling without slipping on a frictionless surface. Hence, we can substitute ωR in the equation of translational kinetic energy into the value of v.
Hard
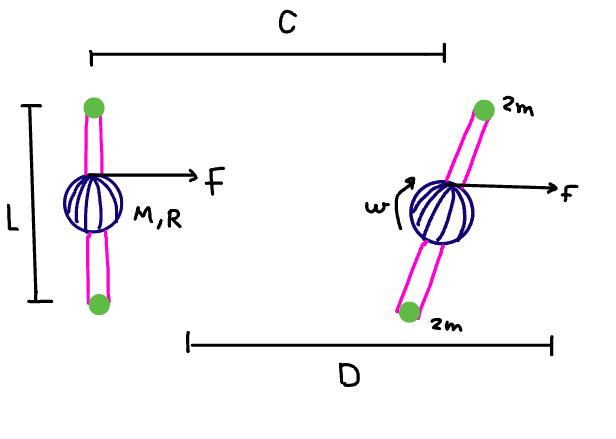
A system consists of a uniform sphere of mass M and radius R. It is attached to the middle of a massless rod of length L, and two small point masses of 2m are at the end of the rod. This apparatus lies on a frictionless surface.
A string is wound up around the sphere, and you start pulling on the string with a constant force of magnitude F, causing the apparatus to slide along the frictionless surface. The entire apparatus also moves a total distance of C. The string that is pulled at force F moves/comes off a total of distance D. The sphere+rod is spinning at an angular speed of ω.
Use the extended system to find what the angular speed ω is in the final state.
Solution:
We know that the change in energy of our extended system is equal to the work of the force on the extended system. We also know that the work of the force on the extended system is equal to the change in translational energy plus the change in rotational kinetic energy. Hence, we start with such equations and set them equal to each other.
However, what is the velocity (v)? We do not know this and must solve for it. We know that the change in the energy of the point particle system is equal to the kinetic translational energy, which is also equal to the work of the force on the point particle system. Hence, by setting such equations equal to each other, we can find v.
Now that we know what the velocity (v) is, we can plug in the representation for v acquired above into the formula for the change in translational kinetic energy. We can also go ahead and find the change in rotational kinetic energy, as seen below.
Lastly, as we now know the change in translational kinetic energy and the change in rotational kinetic energy, we can sum them together and set it equal to the work of the force applied on the extended system. Then, through the manipulation of this equation, we find the answer to the angular speed ω.
Connectedness
1. How is this topic connected to something that you are interested in?
This topic interests me because it involves calculating work in real systems present in the real world, unlike the point particle system which focuses more on calculating work on single atoms or idealized versions of objects modeled as a point particle. Being able to apply physics to real-world situations is always so exciting for me.
This topic is also interesting because one can be able to see how all the various energies come together within the entire system. Unlike the point-particle system where one only considers translational kinetic energy, extended systems go beyond that and consider changes in internal energy. This is very interesting, especially because changes in internal energy sometimes cannot be seen but can be calculated within an extended system.
2. How is it connected to your major?
As a biology major, one can learn how to calculate the work done on an extended system, for example, a Kangaroo jumping. In this case, one is able to incorporate and consider chemical energy changes and thermal energy changes in the Kangaroo. Knowledge of how much energy a Kangaroo uses while jumping is just one example of how one is able to use physics to forward their knowledge in the biology field as well.
As a computer science major, there is a great emphasis on modeling and simulation, including the simulation of real-life scenarios processes. In fact, at Georgia Tech, there is an entire thread dedicated to such an area, which is known as the Modeling and Simulation thread! In this area, individuals utilize computer software and mathematics to model various human behaviors, biological processes, and real-world scenarios and systems. Hence, understanding work and energy for an extended system is important, especially because in extended systems and in the real-world, there are various types of energy to consider. This is not limited to translational kinetic energy, rotational kinetic energy, vibrational potential energy, etc. In a way, extended systems extend (no pun intended) beyond only considering translational kinetic energy (like the point-particle model) to include various types of energy that computer scientists might want to model in order to provide a better computational simulation of a specific process or scenario. Having a strong understanding when it comes to the work and energy of an extended system provides clarity regarding how various energies are being transferred or impacting the system, making the simulation one that is close to real-world processes.
3. Is there an interesting industrial application?
This is a very interesting industrial application because knowing how to calculate the work done on an extended system such as a rocket, could forward our knowledge in rocket science and what is needed to travel further into space. Once we are able to quantify how much work must be done on a system to travel a certain distance at a safe, controlled speed, we have the potential to maybe one day reach Mars and other planets!
See also
Further reading
Chabay, Ruth W., and Bruce A. Sherwood. "9." Matter & Interactions. N.p.: n.p., n.d. N. pag. Print.
For more information on Point Particle and Extended Systems please visit: http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:pp_vs_real
External links
Check out [1] to learn more about Point Particle Systems!
Also take a look at [2] to review more information on Extended (Real) Systems.
To learn more on how Kinetic Energy applies to everyday life: [3]
References
All images used on this page do not belong to me. All problem examples are from the Matter and Interactions Physics book referenced below.
Chabay, Ruth W., and Bruce A. Sherwood. "9." Matter & Interactions. N.p.: n.p., n.d. N. pag. Print.