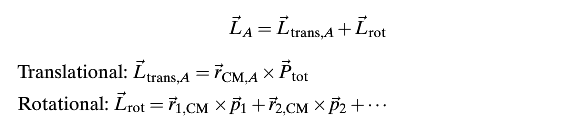Total Angular Momentum
Anthony Yoo Fall 2026
The Main Idea
In the same way it can be convenient to analyze the linear motion of a system via the changes in the linear momentum of the system, it can be useful to use the concept of angular momentum to describe the motion of rotating systems. In general, momentum is a useful concept because it is usually possible to find a system in which the total momentum of the system is conserved - that is, no external force is acting on the system. However, even when momentum isn't conserved, it still provides a useful relationship between the rate of change of an object's motion and the force applied to the object. Angular momentum is useful for this same reason and can be utilized in a similar way.
We can't have angular momentum without an axis
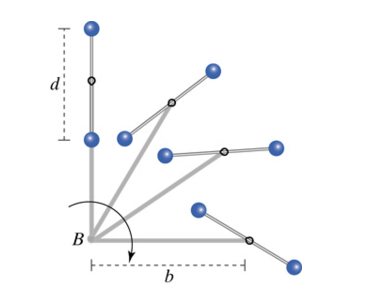
Just like picking a coordinate system for a Free Body Diagram it is important to pick a point where the system rotates. You can pick any point in space; however, it may not really help you much with determining what's actually going to happen in a given situation. If you wanted to be able to predict motion and the effect of torque on motion it is best to pick a point that the system actually will rotate around. Your choice should be relatively simple.
A Mathematical Model
Single Particle Systems
For a single particle revolving about a center of rotation, the angular momentum of the particle is expressed in terms of the particle's translational momentum about the center, as shown below:
- [math]\displaystyle{ \vec{L} = \vec{r}\times\vec{p} }[/math]
Multiparticle Systems
The same technique can also be used to describe the total angular momentum of a multi particle system revolving about a center of rotation. In this case, the total angular momentum is simply the sum of the angular momentum for each particle:
- [math]\displaystyle{ \vec{L_{tot}} = \sum_{j=1}^n \vec{r_j}\times\vec{p_j} }[/math]
Continuous Masses
If you imagine letting the summation for the multiparticle system approach infinity, that is if you were to fill some finite volume with an infinite number of infinitesimally small particles, you would create a continuous distribution of mass rotating about the same central axis. This is how we model the angular momentum of extended objects, or objects that cannot be represented by points. When this is done, you arrive at the following equation:
[math]\displaystyle{ \vec{L} = I\vec{\omega} }[/math]
Here [math]\displaystyle{ I }[/math] is the rotational inertia of the object (For more info see Rotational Inertia) and [math]\displaystyle{ \omega }[/math] is the angular frequency.
It is also Important to note that an object could be treated as a point particle about one axis and an extended object about another, i.e. the Earth rotating while revolving around the sun. In this case, it is useful to separate the object's angular momentum into translational and "spin" components (for more info see Translational & Spin Angular Momentum)
A Computational Model
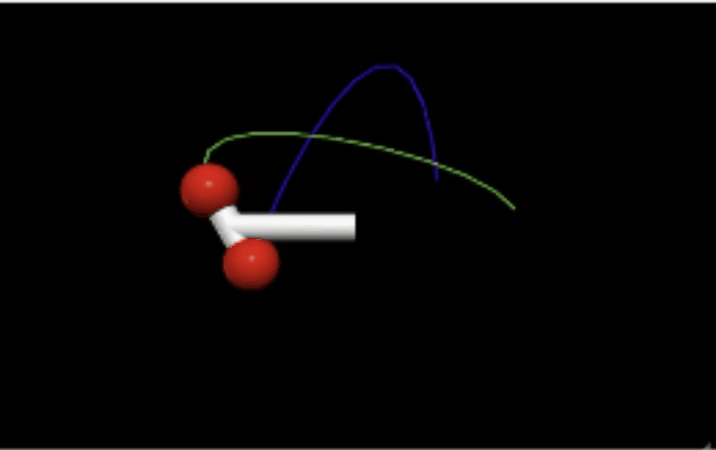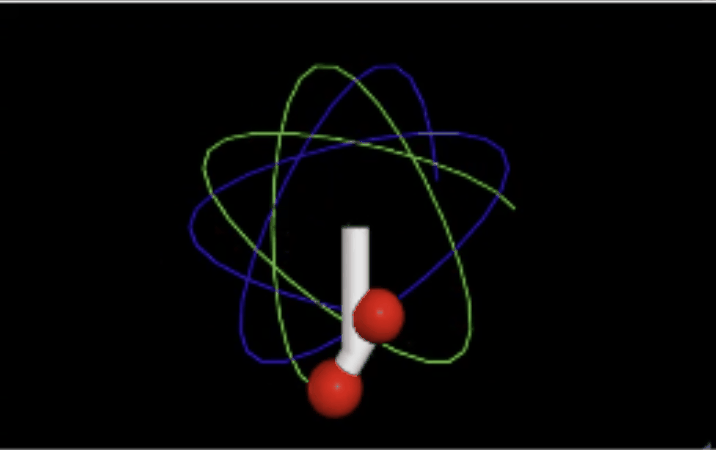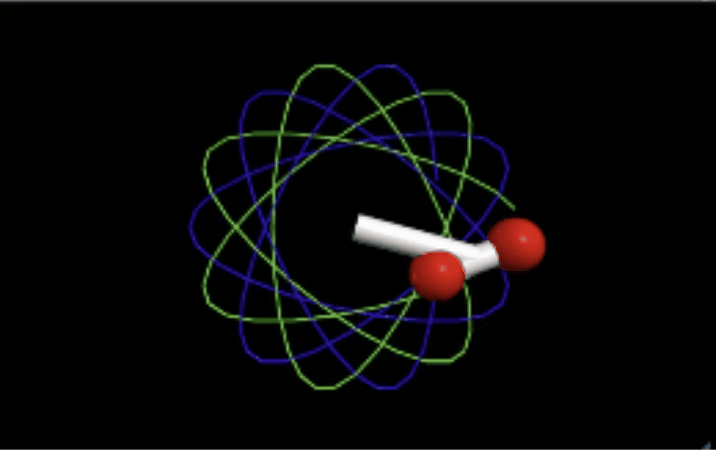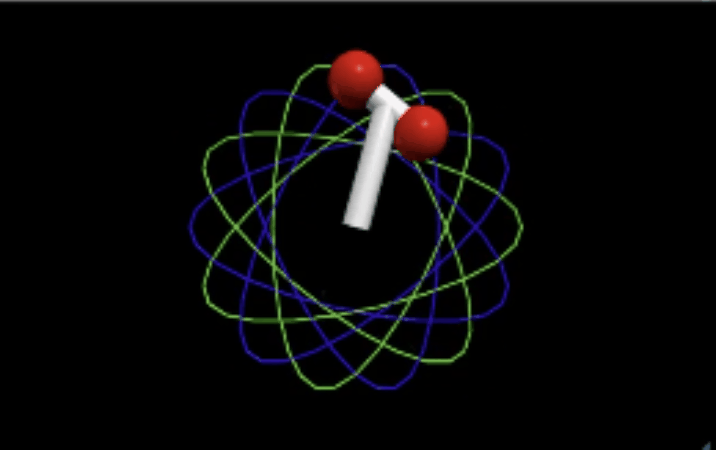
You can visualize this topic of total angular momentum with this code of the total angular momentum of a binary star. You can see the rotational angular momentum along with the translational angular momentum.
This screenshot shows the code in action but you can check it out with this link: https://trinket.io/glowscript/49129c12fd
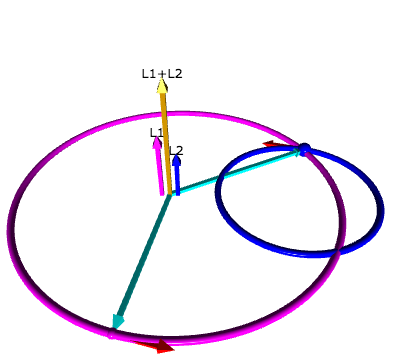
Rotational vs. Translational Angular Momentum
Angular momentum can arise from two physically different types of motion: the motion of a system's center of mass (translational), and the spinning or rotation of the system around its own internal axis (rotational). Many real physical systems contain both types at the same time. This section expands on how these two contributions are defined and how they combine to form the total angular momentum.
Translational Angular Momentum
Translational angular momentum comes from the motion of the system’s center of mass relative to a chosen origin. Even if an object is not spinning, it still has angular momentum if its center of mass moves along a straight or curved path that does not pass through the origin.
The translational contribution is given by:
- [math]\displaystyle{ \vec{L}{trans} = \vec{r}{cm} \times \vec{p}_{cm} }[/math]
where:
[math]\displaystyle{ \vec{r}_{cm} }[/math] is the position of the center of mass relative to the chosen origin
[math]\displaystyle{ \vec{p}{cm} = m\vec{v}{cm} }[/math] is the linear momentum of the entire system
Key idea: Translational angular momentum depends entirely on the center of mass motion and not on any internal rotation.
Rotational Angular Momentum (“Spin”)
Rotational or spin angular momentum comes from an object rotating about an internal axis that passes through its center of mass. This type of angular momentum exists even if the object is not moving through space (i.e., the center of mass is stationary).
It is given by:
- [math]\displaystyle{ \vec{L}_{rot} = I\vec{\omega} }[/math]
where:
[math]\displaystyle{ I }[/math] is the rotational inertia about the axis through the center of mass
[math]\displaystyle{ \vec{\omega} }[/math] is the angular velocity vector
Key idea: Rotational angular momentum describes the internal spinning motion of the object.
Total Angular Momentum
For extended bodies or multi-part systems, the total angular momentum is the vector sum of the translational and rotational contributions:
- [math]\displaystyle{ \vec{L}{total} = \vec{L}{trans} + \vec{L}_{rot} }[/math]
This decomposition is extremely useful in physics because:
Some problems only involve [math]\displaystyle{ \vec{L}_{trans} }[/math] (e.g., a thrown ball that is not spinning).
Others only involve [math]\displaystyle{ \vec{L}_{rot} }[/math] (e.g., a spinning disk fixed at its center).
Most real systems involve both (e.g., planets rotating while orbiting, wheels rolling without slipping, gymnasts flipping).
Understanding which type of angular momentum is present helps determine what torques act on the system and whether the total angular momentum is conserved.
Examples
These examples will help to solidify the difference between the different components of total angular momentum.
Simple
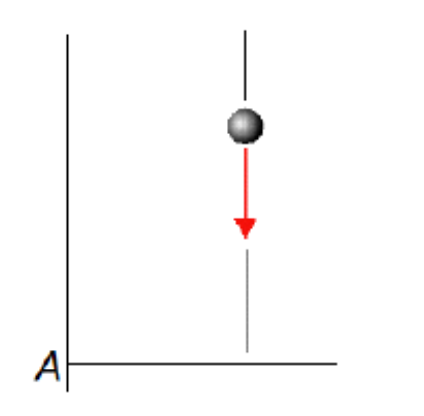
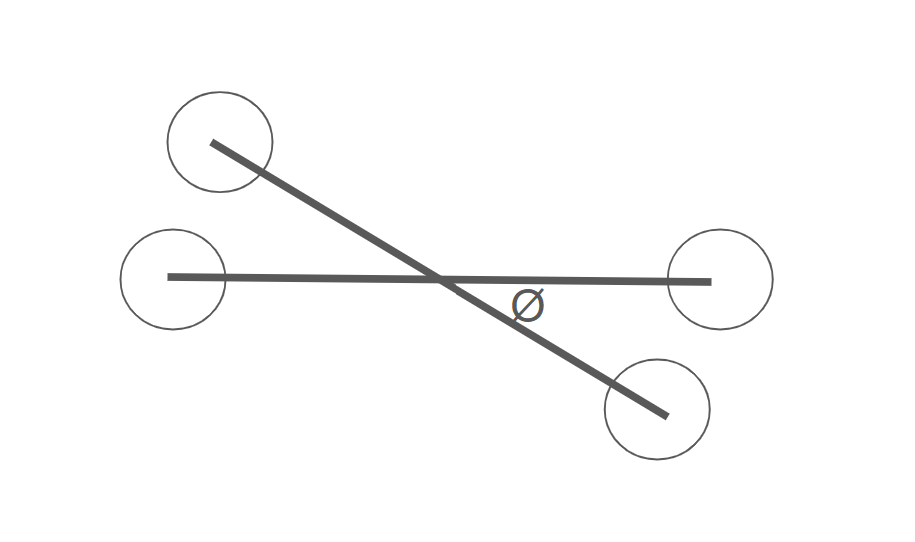
A ball falls straight down in the xy plane. Its momentum is shown by the red arrow. What is the direction of the ball's total angular momentum about location A?
When attempting to solve this question, it is important to recognize that there is no rotational angular momentum, because there is no rotation about the center of mass. The only thing that is happening is that the center of mass is translating from some point A. In this case since there is only translational angular momentum, we would simply find the direction of the total angular momentum by using our right hand rule [hint: r points from A to the ball, and the momentum is pointing in the -y direction]
The direction of the ball's total angular momentum is in the -z direction.
Middling
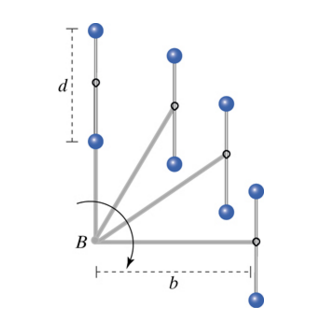
This example shows the importance of understanding the difference between rotational and translational angular momentum.
a) Calculate Lrot (both magnitude and direction)
b) Calculate Ltrans,B (both magnitude and direction)
c) Calculate Ltotal,B (both magnitude and direction)
Due to the fact that...
We calculated that our Lrot is zero, our total angular momentum is just based on translational angular momentum. So in this case, total angular momentum = translational angular momentum. So total angular momentum is 9.72 kgm^2/s, with the same direction, into the page.
Difficult
This problem shows an example of total angular momentum being based off both translational angular momentum and rotational angular momentum.
a) Calculate Lrot (both magnitude and direction)
b) Calculate Ltrans,B (both magnitude and direction)
c) Calculate Ltotal,B (both magnitude and direction)
The total angular momentum is rotational + translational so it is <0,0,-11.16> kgm^2/s
Computational Model for this problem
Here the angular momentum points in the negative z-hat direction because the masses are moving clockwise (both Ltrans and Lrot)
In order to update the positions of the masses in this computational model, you need to find the new position of the masses with respect to the center that it is rotating around (in this case it is the axis which we used to calculate lrot) and you need the new position of the rod that is rotating.
To calculate the new position of the masses with respect to the axis they are rotating around (Lrot), we need to find the change in angle between the last iteration and the new one, then we need to use trig.
To find the new angle we can take the old angle and add it to w * deltat
- [math]\displaystyle{ \theta_{f} = \theta_{i} + \vec{w_{2}}\times \Delta t }[/math]
Now, the new position of the mass 1 is just
- [math]\displaystyle{ \vec{r_{mc2}} = \lt d/2(cos(\theta), d/2sin(\theta), 0)\gt }[/math]
For Mass 2, it's the same but with an angle that is 180 degrees less than theta.
Now we have to find the arrangement of the first cylinder.
- [math]\displaystyle{ \theta_{f} = \theta_{i} + \vec{w_{1}} \times \Delta t }[/math]
- [math]\displaystyle{ \vec{r_{cyl}} = \lt b(sin(\theta)), b(cos(theta)), 0\gt }[/math]
Then the positions of the two masses are just these two vectors added together.
- [math]\displaystyle{ \vec{r_{m}} = \vec{r_{cyl}} + \vec{r_{mc2}} }[/math]
The link to the code:
https://www.glowscript.org/#/user/danielisme18/folder/MyPrograms/program/angularMomentump1
History
Newton, in the Principia, hinted at angular momentum in his examples of the First Law of Motion,
"A top, whose parts by their cohesion are perpetually drawn aside from rectilinear motions, does not cease its rotation, otherwise than as it is retarded by the air. The greater bodies of the planets and comets, meeting with less resistance in more free spaces, preserve their motions both progressive and circular for a much longer time." However, his geometric proof of the Law of Areas is an outstanding example of Newton's genius, and indirectly proves angular momentum conservation in the case of a central force.
In 1736 Euler, like Newton, touched on some of the equations of angular momentum in his Mechanica without further developing them.
Bernoulli wrote in a 1744 letter of a "moment of rotational motion", possibly the first conception of angular momentum as we now understand it.
In 1799, Pierre-Simon Laplace first realized that a fixed plane was associated with rotation — his invariable plane.
Louis Poinsot in 1803 began representing rotations as a line segment perpendicular to the rotation, and elaborated on the "conservation of moments".
In 1852 Léon Foucault used a gyroscope in an experiment to display the Earth's rotation.
William J. M. Rankine's 1858 Manual of Applied Mechanics defined angular momentum in the modern sense for the first time:
"...a line whose length is proportional to the magnitude of the angular momentum, and whose direction is perpendicular to the plane of motion of the body and of the fixed point, and such, that when the motion of the body is viewed from the extremity of the line, the radius-vector of the body seems to have right-handed rotation."
See also
Further reading
Books and other print media that cover this topic in more depth:
Elementary Theory of Angular Momentum (Dover Books on Physics) by M.E. Rose
Matter and Interactions by Ruth W. Chabay and Bruce A. Sherwood
http://chaos.utexas.edu/wp-uploads/2012/03/Angular_Momentum_21.pdf
Video Content
Videos on Total Angular Momentum:
https://www.youtube.com/watch?v=8SfRmqSQENU&index=34&list=PL9HgJKLOnKxedh-yIp7FDzUTwZeTeoR-Y
https://www.youtube.com/watch?v=nFSMu3bxXVA
https://www.youtube.com/watch?v=diZDoY07LG4
https://www.youtube.com/watch?v=iWSu6U0Ujs8
External links
These are some internet articles that can show more animations and pictures to help understand this concept
http://www.phy.duke.edu/~lee/P53/sys.pdf
http://farside.ph.utexas.edu/teaching/301/lectures/node120.html
https://www.physics.purdue.edu/webapps/index.php/course_document/index/phys172/1332/135/9703
http://www.sparknotes.com/testprep/books/sat2/physics/chapter10section6.rhtml
http://hyperphysics.phy-astr.gsu.edu/hbase/amom.html
References
https://www.chegg.com/homework-help
http://www.sparknotes.com/physics/rotationalmotion/angularmomentum/section1.rhtml
http://www.phy.duke.edu/~lee/P53/sys.pdf
http://farside.ph.utexas.edu/teaching/301/lectures/node120.html
https://www.physics.purdue.edu/webapps/index.php/course_document/index/phys172/1332/135/9703
http://hyperphysics.phy-astr.gsu.edu/hbase/amom.html
http://www.sparknotes.com/testprep/books/sat2/physics/chapter10section6.rhtml
Professor Gumbart [Georgia Institute of Technology] Lecture Notes
Matter and Interactions 4th edition. Full Citation: Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print.