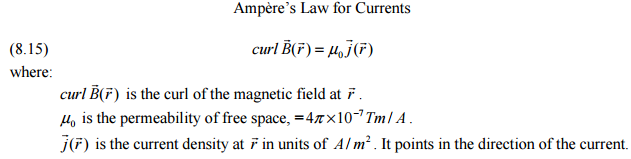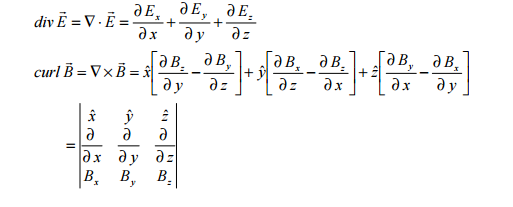The Differential Form of Ampere's Law
Many physical laws taught in Physics I and II are only correct at non-relativistic speeds (where the speed is much less than the speed of light). This is caused by a phenomenon known as "relativistic retardation" that refers to the fact that changes in magnetic and electric fields propagate at the speed of light and, therefore, cannot be measured instantaneously. Typically, this is not an issue if the particles are moving much slower than the speed of light because the error between non-relativistic forms of physical laws is often so small that it is irrelevant. As particles approach speeds close to the speed of light these differences can become significant and methods for finding electric or magnetic fields (such as the Biot-Savart law) are no longer accurate. This is not true for Ampere's Law which makes it useful for problems involving particles moving at near light speeds.
Curl
To have a model that is consistent with the theory of relativity, the property of a magnetic field called the "curl" must be utilized. The curl is the path integral of magnetic field per unit area, in the limit as the area goes to zero. This is useful because its value is proportional to the current density at the same location and time so there is an established relationship. This relationship is known as a "local" relationship because both are evaluated at the same place and time. This also demonstrates how Ampere's Law is relativistically correct because this local relationship isn't effected by relativistic retardation.
Lecture Video: https://www.youtube.com/embed/mj2ahFjnpmY
A Mathematical Model
Curl is the measurement of how much magnetic field loops around a line. It is a vector in the same direction of the flow of current.
Curl can also be expressed in terms of a "del" operator or gradient operator. This is the same operator that relates the (x, y, z) components of electric field to voltage. Expressing the components as the the partial derivative of voltage is the gradient of it.
A Computational Model
Model of Curl Around a Wire with Conventional Current Moving Out of the Screen
Glowscript link: https://trinket.io/glowscript/7c5c057c59?toggleCode=true
The direction of curl is given by the right hand rule by putting your thumb in the direction of the current. The way your hand curls is the way the magnetic field curls.
Examples
Connectedness
In Biomedical Engineering
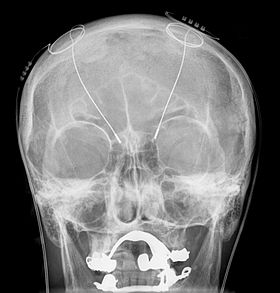
X-Ray of a patient with Deep Brain Stimulation. Attribution: https://en.wikipedia.org/wiki/Deep_brain_stimulation
The differential form of Ampere's is simply another way of representing Ampere's Law and therefore does not differ from the integral form of Ampere's Law in its applications. In the field of biomedical engineering, the application of Ampere's Law in advanced computational models of the human brain may one day lead to a better understanding of the electromagnetic effects that the activation of one neuron may have on an adjacent neuron. On a slightly larger scale, deep brain stimulation procedures involve the use of implantable electrodes to electrically stimulate targeted areas of the brain for the treatment of neurological illnesses such as Parkinsons' disease. Knowledge of Ampere's Law would imply that the use of one of these electrodes in the brain creates a curling magnetic field around the electrode that could affect neurons outside of those being intentionally targeted.
In Mechanical Engineering
- The differential form of Ampere's Law interests me because it is one of the first laws that we learned that is relativistically correct, although it is not the complete form of Ampere's Law.
- As a ME major I imagine Ampere's Law will pop up again in either fluids or thermodynamics.
- An interesting application of Ampere's Law is in MRI machines to be able to find the magnetic field around a loop.
See also
- Gauss's Law
- The Integral form of Ampere's Law
- Gradient Operations
Further reading
- http://www.physnet.org/modules/pdf_modules/m138.pdf
- http://ww3.haverford.edu/physics-astro/songs/ampere.PDF
References
- http://www.physics.byu.edu/faculty/rees/220/book/Lesson8.pdf
- Matter and Interactions, 4th Edition
- Deep Brain Stimulation (WebMD): http://www.webmd.com/parkinsons-disease/guide/dbs-parkinsons#1