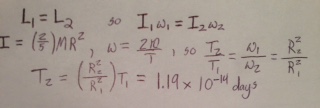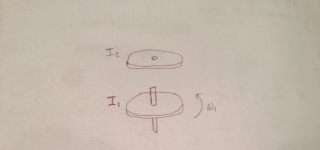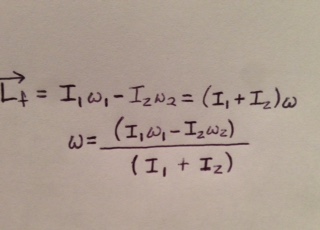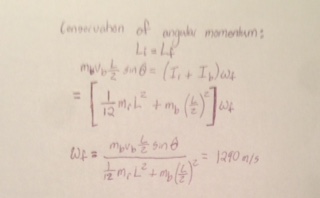Systems with Zero Torque
Claimed by Yash Shelar (Fall 2024).
Systems with Zero Torque
The Main Idea
In physics, torque is the measure of the rotational force applied to an object. A system with zero torque occurs when the sum of all torques acting on an object is zero, resulting in no rotational acceleration. These systems are fundamental in understanding equilibrium and rotational dynamics.
A Mathematical Model
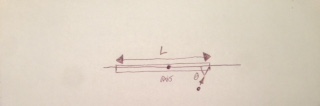
Torque ([math]\displaystyle{ \tau }[/math]) is defined as the cross product of the radius vector ([math]\displaystyle{ \vec{r} }[/math]) and the force vector ([math]\displaystyle{ \vec{F} }[/math]):
[math]\displaystyle{ \tau = \vec{r} \times \vec{F} = rF\sin\theta, }[/math]
where:
- [math]\displaystyle{ r }[/math] is the distance from the pivot point to the point where the force is applied,
- [math]\displaystyle{ F }[/math] is the magnitude of the force,
- [math]\displaystyle{ \theta }[/math] is the angle between the radius vector and the force vector.
An alternative interpretation for torque magnitude can be thought of by drawing a line parallel to the force ([math]\displaystyle{ \vec{F} }[/math]) passing through the point where ([math]\displaystyle{ \vec{F} }[/math]) is applied to our system. This line is called the line of action or the line of application. The distance of closest approach of this line to the axis, or in other words, the shortest distance from this line to the axis, is the magnitude ([math]\displaystyle{ |\vec{F}|\sin\theta, }[/math]), which is also called the moment arm or lever arm, symbolized by ([math]\displaystyle{ r_{\perp} }[/math])
For a system to have zero torque:
1. The sum of all torques about any axis must equal zero:
[math]\displaystyle{ \sum \tau = 0. }[/math]
2. Forces must act such that they produce no net rotational effect.
These principles form the basis for analyzing systems in static or rotational equilibrium, such as beams supported at both ends or balanced seesaws.
It follows from the angular momentum principle, [math]\displaystyle{ LA_{f} = LA_{i} + r_{net} \cdot \Delta t }[/math] that for systems with zero torque, [math]\displaystyle{ LA_{f} = LA_{i} }[/math].
A Computational Model
To model systems with zero torque computationally:
- Define all forces [math]\displaystyle{ F_i }[/math] and their respective positions [math]\displaystyle{ r_i }[/math].
- Calculate the torque contributions from each force: [math]\displaystyle{ \tau_i = r_i \times F_i. }[/math]
- Ensure the sum of torques equals zero: [math]\displaystyle{ \sum \tau_i = 0. }[/math]
Inputs and Outputs
- Inputs:
* Positions of forces [math]\displaystyle{ r_i }[/math], magnitudes and directions of forces [math]\displaystyle{ F_i }[/math], angles [math]\displaystyle{ \theta_i }[/math].
- Outputs:
* Confirmation of equilibrium or required adjustments to achieve equilibrium.
Implementation
The following GlowScript code demonstrates how to verify a system with zero torque:
from vpython import *
def calculate_torque(forces, positions, angles):
total_torque = 0
for i in range(len(forces)):
torque = positions[i] * forces[i] * sin(radians(angles[i]))
total_torque += torque
return total_torque
# Example inputs
<pre>
forces = [10, 20, 15] # Magnitudes of forces in Newtons
positions = [2, 1.5, 3] # Distances from the pivot in meters
angles = [90, 45, 135] # Angles between force and radius vectors in degrees
total_torque = calculate_torque(forces, positions, angles)
if abs(total_torque) < 1e-5:
print("System is in equilibrium: Zero Torque")
else:
print("System is not in equilibrium. Adjust forces or positions.")
Examples
Simple
Consider a seesaw with a pivot at its center:
- Child A (mass [math]\displaystyle{ m_A = 30\,\mathrm{kg} }[/math]) sits 2 meters to the left of the pivot.
- Child B (mass [math]\displaystyle{ m_B = 20\,\mathrm{kg} }[/math]) sits 3 meters to the right of the pivot.
The torque calculation:
[math]\displaystyle{ \tau_A = -m_A g r_A = -30 \cdot 9.8 \cdot 2 = -588\,\mathrm{N\cdot m}, }[/math]
[math]\displaystyle{ \tau_B = m_B g r_B = 20 \cdot 9.8 \cdot 3 = 588\,\mathrm{N\cdot m}. }[/math]
Since [math]\displaystyle{ \tau_A + \tau_B = 0 }[/math], the system is in equilibrium.
Middling
Analyze a horizontal beam with a weight of 50 N placed at the center and two supports at either end. Use the principles of zero torque to determine the forces exerted by the supports.
Difficult
Evaluate a rotating platform with multiple forces acting at different radii and angles. Computationally solve for equilibrium by iterating through various force configurations.
Extra
1. Suppose that a star initially had a radius about that of our Sun, 7x10^8km, and that it rotated every 26 days. What would be the period of rotation if the star collapsed to a radius of 10km?[1]
Solution:
2. An arrangement encountered in disk brakes and certain types of clutches is shown here. The lower disk. The lower disk, of moment of Inertia I1, is rotating with angular velocity 1. The upper disk, with moment of inertia I2, is lowered on to the bottom disk. Friction causes the two disks to adhere, and they finally rotate with the same angular velocity. Determine the final angular velocity if the initial angular velocity of the upper disk 2 was in the opposite direction as 1.
Solution:
3. A uniform thin rod of length 0.5 m and mass 4.0 kg can rotate in a horizontal plane about a vertical axis through its center. The rod is at rest when a 3.0 g bullet traveling the horizontal plane is fired into one end of the rod. As viewed from
above, the direction of the bullet’s velocity makes an angle of 60o with the rod. If the bullet lodges in the rod and the angular velocity of the rod is 10 rad/s immediately after the collision, what is the magnitude of the bullet’s velocity just before
the impact? [2]
Solution:
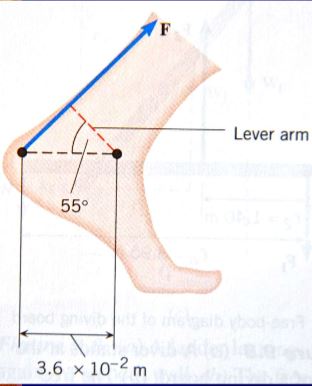
4. The tendon in your foot exerts a force of magnitude 720N. Determine the Torque (magnitude and direction)of this force about the ankle joint:
5. A woman whose weight is 530N is poised at the right end of a diving board with a length of 3.90 m. The board has negligible weight and is bolted down at the left end, while being supported 1.40m away by a fulcrum. Find the forces that the bolt and the fulcrum respectively exert on the board.

6. A 5.0m long horizontal beam weighing 315N is attached to a wall by a pin connection that allows the beam to rotate. Its far end is supported by a cable that makes an angle of 53 degrees with the horizontal, and a 545 N person is standing 1.5m from the wall. Find the force in the cable, Ft, and the force is exerted on the beam by the wall, R, if the beam is in equilibrium.
Connectedness
The principles of zero torque connect to broader physics topics such as static equilibrium, rotational dynamics, and moments of inertia. Applications include engineering structures, robotics, and biomechanics.
This principle directly relates to the bio-mechanical techniques used by various types of athletes, it can thus for example be incorporated into a physical analysis of extreme sports. Athletes (figure skaters, skateboarders, etc.) are able to employ this principle to increase the rates of rotation of there bodies without having to generate any net force. Given that [math]\displaystyle{ L_{tot} = L_{trans} + L_{rot} }[/math], and assuming that a change in [math]\displaystyle{ L_{trans} }[/math] is trivial, it follows that [math]\displaystyle{ L_{rot, f} = L_{rot, i} }[/math]. Specifically, [math]\displaystyle{ \omega_{f} \cdot I_{f} = \omega_{i} \cdot I_{i} }[/math]. This relation implies that the athlete in question should be able to either increase or reduce their angular velocity by decreasing or increasing his or her moment of inertia respectively. Generally, this is accomplished by voluntarily cutting the distance between bodily appendages and the athlete's center of mass. In the example of a figure skater for instance, the moment of inertia is decreased by bringing in the arms and legs closer to the center of the body. Additionally, the athlete might crouch down in order to further decrease the total distance from his or her body’s center of mass. As a result, an inversely proportional change in the angular velocity of the athlete’s motion will occur, causing the speed of the athletes rotation either increase or decrease. [3]
[4]
An immediate industrial example of a zero-torque system is alluded to in example problem two above. The zero-torque system is a very important method of abstraction in the field of control systems engineering. In particular, this perspective is instrumental for calculating selection factors for clutching and braking systems. Though often offered as separate components, their function are often combined into a single unit. When starting or stopping, they transfer energy between an output shaft and an input shaft through the point of contact. By considering the input shaft, output shaft and engagement mechanism as a closed system, researchers are enabled to make calculations that can inform them on how to engineer systems of progressively greater efficiency in regard to the mechanical advantage unique to different type of engagement system.[5] 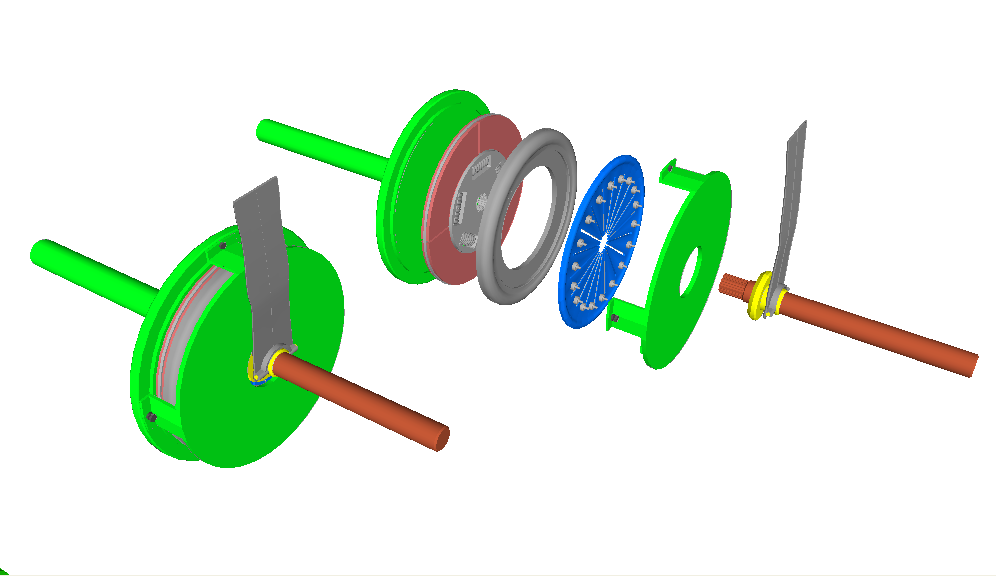 [6]
[6]
History
The concept of torque and equilibrium dates back to the development of classical mechanics. Archimedes' studies of levers laid the groundwork for understanding rotational forces. Modern physics extends these principles to complex systems and computational modeling.
The empirical analysis of what might now be described as “zero-torque systems” by various natural philosophers pointed towards the principles of angular momentum and torque long before they were formulated in Newton’s Principia. The principle of torque was indicated as early as Archimedes (c. 287 BC - c.212 BC) who postulated the law of the lever. As written below, it essentially describes an event in which zero net torque on a system results in zero angular momentum(4).[7] Much later on in 1609, the astronomer Johannes Kepler announced his discovery that planets followed an elliptical pattern around the Sun. Specifically, he claimed to have found that "a radius vector joining any planet to the sun sweeps out equal areas in equal lengths of time." Mathematically, this area, [math]\displaystyle{ \frac{1}{2} \cdot r \cdot v \cdot sin(\theta) }[/math] is proportional to angular momentum [math]\displaystyle{ r \cdot v \cdot sin(\theta) }[/math]. It was Newton's endeavor to find an analytical solution for Kepler’s observations that lead to the derivation of his second law, The Momentum Principle, in the late 1600s.[8]
See also
http://www.physicsbook.gatech.edu/The_Moments_of_Inertia http://www.physicsbook.gatech.edu/Systems_with_Nonzero_Torque http://www.physicsbook.gatech.edu/The_Angular_Momentum_Principle http://www.physicsbook.gatech.edu/Torque http://www.physicsbook.gatech.edu/Predicting_the_Position_of_a_Rotating_System
Further reading
- Serway, R. A., & Jewett, J. W. Physics for Scientists and Engineers (10th Edition).
- Halliday, D., Resnick, R., & Walker, J. Fundamentals of Physics (11th Edition).
- Matter and Interactions, 4th edition, Volume 1.
External links
- Khan Academy - Physics
- HyperPhysics - Torque
- https://www.khanacademy.org/science/physics/torque-angular-momentum/torque-tutorial/v/constant-angular-momentum-when-no-net-torque
- https://www.youtube.com/watch?v=whVCEIfTT0M
- https://www.youtube.com/watch?v=jeB4aAVQMug
References
- ↑ Browne, Michael E. "Angular Momentum." Physics for Engineering and Science. Third ed. McGraw Hill Education, 2013. 134. Print.
- ↑ https://www.physics.ohio-state.edu/~gan/teaching/spring99/C12.pdf.Retrieved December 3, 2015.
- ↑ Chabay, Ruth W., and Bruce A. Sherwood. "Angular Momentum." Matter & Interactions. 4rth ed. Vol. 1 : Modern Mechanics. Hoboken, NJ: Wiley, 2012. 434,440. Print.
- ↑ http://qctimes.com/news/local/young-ice-skaters-shine-at-u-s-figure-skating-event/image_37e22f34-2c3a-5445-84cb-54972b525ad8.html. Retrieved December 3.2015.
- ↑ http://www.controleng.com/single-article/selection-factors-for-clutches-amp-brakes/9fbd9f3d184754e5ced13817eff2c659.html. Retrieved December 3, 2015.
- ↑ https://upload.wikimedia.org/wikipedia/commons/f/fa/Car_clutch.png. Retrieved December 3, 2015.
- ↑ http://www.britannica.com/biography/Archimedes. Retrieved December 3. 2015.
- ↑ Chabay, Ruth W., and Bruce A. Sherwood. "Angular Momentum." Matter & Interactions. 4rth ed. Vol. 1 : Modern Mechanics. Hoboken, NJ: Wiley, 2012. 434,440. Print.