Standing Waves

From Physics Book
Jump to navigation Jump to search

Claimed by Shubhangi Asthana, Fall 2023

Resonance

Resonance is the physical phenomenon in which a system vibrates in response to an applied frequency, but the external force of this frequency interacts with the object in such a way that it causes the system to oscillate with a maximum amplitude due to the specific frequency induced. This property applies to many fields of physics when studying the way an object behaves in certain situations.

Natural Frequencies

When dealing with sound and its interaction with various objects in space, a resonant frequency of a wave is the natural frequency of vibration determined by the physical and chemical properties of said object.The existence of resonance in and of itself depends on the existence of natural frequencies. Objects often have multiple natural vibrating resonant frequencies, and it will pick out those frequencies from a series of excitations, making it an even more useful tool when identifying the properties of an object.

History

One of the most famous visible examples of resonance in history is the disaster at the Tacoma Narrows Bridge in 1940. This bridge, in Tacoma, Washington, spanned the Tacoma Narrows Strait, but it collapsed into the waters of Puget Sound on November 7, 1940. This bridge had such a short lived existence due to resonance. Since its construction, workers observed vertical movement in the suspension bridge on windy days. This brought about the origin of the bridge's nickname: "Galloping Gertie". However, on a particularly windy day, the wind provided the bridge with a periodic vibrating frequency that matched the bridge's natural vibrational frequency, causing the bridge to become a massive oscillating standing wave. This intense oscillation proved too much for the structural integrity of the bridge, and it collapsed. No human lives were lost in the accident, but a black, male cocker spaniel named Tubby passed away from the incident.

Standing Waves

A standing wave is formed when two waves similar in speed, wavelength, and amplitude, moving in opposite directions, intersect.

Constructive Interference: occurs when two or more waves meet and their displacements are in the same direction.

  • The amplitude of the resulting wave is the vector sum of the amplitude of the individual waves.
  • This happens when the peaks (crests) of one wave align with the peaks of another wave, or when the troughs align with troughs.
  • In a standing wave, this temporary point is known as an antinode.
  • The phase difference between the waves is either zero or an integer multiple of 2π or a full wavelength.

Destructive Interference: occurs when two or more waves meet and their displacements are in opposite directions.

  • The amplitude of the resulting wave is less than at least one of the individual waves.
  • This happens when the peak of one wave aligns with the trough of another wave.
  • In a standing wave, this fixed point is called a node.
  • The waves are out of phase with each other, typically by a phase difference of π or half a wavelength.

Some important properties of standing waves include the following:

  • The peaks, also known as crests of a standing wave, are stationary.
  • All the points between consecutive nodes are in phase, meaning they have the same velocity.
  • There is no net energy transfer in a standing wave as the waves travel in opposite directions.
  • The ends of standing waves are always either nodes or antinodes.

A Visual Model Model/ Standing Wave Simulation

Standing Wave. Licensed under Creative Commons Attribution-Share Alike 4.0 International. By Francisco Esquembre.
Standing Wave. Licensed under Creative Commons Attribution-Share Alike 4.0 International. By Francisco Esquembre.


A Mathematical Model

When delving into the mathematics of standing waves, we can examine scenarios involving both ends of a cylinder being closed, both ends being open, or one end being closed while the other is open.

For cylinders with both ends either closed or open, the mathematical equations for standing waves are identical. In a cylinder with closed ends, the ends of the waves are nodes, where there is no movement. On the other hand, with open ends, the wave ends are antinodes, where the maximum movement occurs. The longest wavelength and lowest frequency standing wave is referred to as the first harmonic. With each subsequent harmonic, the frequency goes up, and the wavelength gets shorter.

We can describe the wavelength-length relationship for a string's standing waves with the equation:

λn = 2L⁄n

Where λ_n is the wavelength, L is the length of the string, and n represents the harmonic number.

The standing wave's frequency is calculated using:

f = v / λn

Here, v is the wave's velocity, and the first harmonic's frequency is the fundamental frequency. Each higher harmonic's frequency is a whole-number multiple of this fundamental frequency.

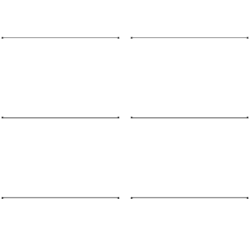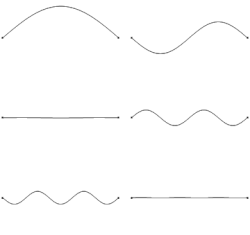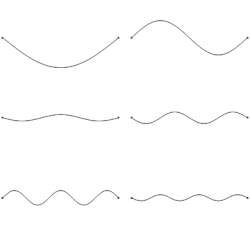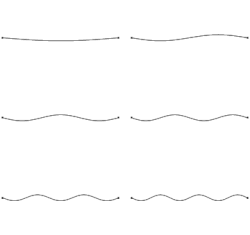
Harmonics of standing wave with closed ends
Harmonics of standing wave with closed ends

In a cylinder with one closed and one open end, the standing wave will form a node at the closed end and an antinode at the open end, leading to the wave's length being a quarter of its wavelength. Adjusting the equation for the wavelength of a standing wave in a cylinder with two closed or open ends to accommodate the quarter wavelength change, we get a new formula:

λn = 4L⁄n

Standing wave with one fixed and one free end
Standing wave with one fixed and one free end


A helpful diagram to understand the harmonics of standings waves is the following:

Harmonics
Header text Header text
Both ends fixed λn = 2L⁄n n = 1, 2, 3, 4..
Both ends free λn = 2L⁄n n = 1, 2, 3, 4..
One end free, one end fixed λn = 4L⁄n n = 1, 3, 5...


Applications

The applications of standing waves can be encountered in ample examples from our daily lives.

  • The most obvious example would perhaps be a guitar string. With both ends fixed, the frequency of the sounds produced upon plucking a guitar is determined by the length of the string. Instruments such as flutes and organ pipes also produce sound through the concept of standing waves, however, the waves in this case are formed by the movement of the air as opposed to a string.
  • Another example of standing waves is the notice cancellation function in headphones, which is achieved by total destructive interference so that there is no resulting amplitude and no resulting sound.
  • Standing waves can be encountered on the surface of the Earth as seismic waves, which can cause earthquakes.
  • Kundt's tube is an acoustical apparatus that takes advantage of the concept of standing waves to measure the speed of time in a gas and solid rod. Now it is funnily enough used to demonstrate the concept of standing waves in physics laboratories.
  • A tuning fork, as you will see below, can also cause a standing wave due to its back-and-forth oscillations. When a tuning fork is struck, it vibrates at its own natural frequency. If this frequency matches the resonant frequency of an air column in a pipe, the air column starts to resonate, and a loud standing forms within the pipe.

Strings

Easy

A standing wave is generated on a string fixed at both ends. The first harmonic frequency of this wave is 180 Hz. Determine the string's length and the wavelength of the sound produced if the wave travels on the string at 260 m/s and the speed of sound in air is 360 m/s. For the string's length and the sound's wavelength:

  • The string length is given by: L = v⁄2f = 260 m/s⁄2 × 180 Hz ≈ 0.72 m
  • Wavelength: λ = vair⁄f = 360 m/s⁄180 Hz = 2.0 m

A tube has one end open and the other end closed. Compute the ratio of the frequency of the first harmonic to the frequency of the third harmonic.

  • For the frequency ratio in a tube with one closed and one open end: Ratio = f1⁄f3 = 5:1

Hard: Application

A tube with one end open and the other closed is used in an experiment with sound. If a sound source with a frequency of 2500 Hz is placed at the open end and a fine powder inside the tube forms heaps at intervals of 9.0 cm when the sound is on, explain why this happens and use the information to estimate the speed of sound.

  • The sound from the source creates a standing wave inside the tube. The powder gathers at the nodes, the points of no movement in the standing wave, because the air at the antinodes (points of maximum movement) pushes the powder away. Since the distance between nodes is half the wavelength, the heaps indicate the nodes.
  • The distance between the nodes is half the wavelength of the sound wave. Given that the distance between the heaps (which indicates the node distance) is 9.0 cm, the full wavelength (λ) is twice this distance, which is 18.0 cm or 0.18 m. The speed of sound (v) is the product of the frequency (f) and the wavelength (λ). So, λ = 2 × d = 2 × 0.09 m. Given that v = f × λ, we can substitute our known values into the equationv = 2500 Hz × 0.18 m which gives 450 m/s. This matches the textbook value of the speed of sound!

Tuning Forks

A cylindrical tube open at both ends is submerged in water. When a tuning fork with a frequency of 440 Hz is activated above the tube, a distinct sound is heard, indicating a resonance. This occurs when the air column in the tube is at its minimum length for resonance. Given that the speed of sound is 345 m/s, calculate: a. The minimum length of the air column in the tube. b. The minimum distance the tube must be lifted for the next resonance to be heard while the same tuning fork is still in use.

  • To find the minimum length of the air column in the tube for resonance with a 440 Hz tuning fork and a sound speed of 345 m/s, we use the formula for the first harmonic in an open tube, which is half of the wavelength. The wavelength (λ) is the speed of sound divided by the frequency. Thus, the length (L) is half of that wavelength. So, L = v⁄2f or L = 345⁄2 × 440 ≈ 0.392 meters.
  • The tube has to be raised by a distance equal to half of the wavelength to hear the next loud sound. Thus, Distance = λ⁄2. This distance is the same as the length we found for the first resonance. So, Distance = λ⁄2 or Distance = 345⁄2 × 440 ≈ 0.392 meters.

Connectedness

Standing waves have many important applications in physics, especially quantum physics!

See also

Further reading

External links

References

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Standing_Waves&oldid=42097"