claimed by Madhur Bhuyan Spring 2017

Spring Force is the non-constant, elastic force exerted by a spring upon a system.

The Main Idea

The spring force models the force in a system due to the presence of a stretched or compressed spring. This force is based upon two factors of the spring: the spring's stiffness and the distance the spring has been stretched. The spring's stiffness is a constant that represents how much force is required to stretch or compress a spring over a certain distance. The distance the spring has been stretched is measured relative to the length of the spring at its relaxed length. This length is the length the spring exhibits when the net forces acting upon the spring are zero.

The most important thing to remember about the spring force is that it is a non-constant force. The magnitude of the force varies based on how much the spring is being stretched or compressed, as displayed in the following mathematical model.

A Mathematical Model

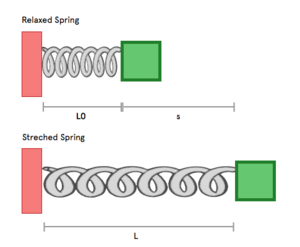
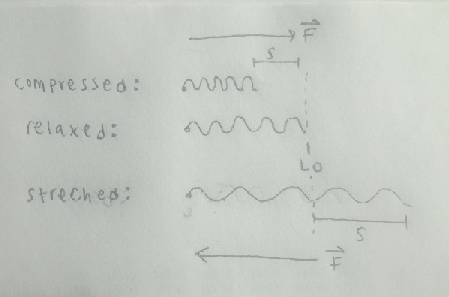
L0 is the distance in the relaxed length, while L is the distance of the entire spring. s is the difference between these two variabels.

The magnitude of the spring force is represented by the equation [math]\displaystyle{ \vert \vec{F}_{spring} \vert = k_s \vert s \vert }[/math], where [math]\displaystyle{ \vert s \vert }[/math] is the absolute value of the stretch of the spring [math]\displaystyle{ s = L - L_0 }[/math], where the force of the spring is directly proportional to the extension of the spring. In other words, if you pull on the spring a lot, the force will be strong; if you pull on the spring a little, the force will be weak.

[math]\displaystyle{ L_0 }[/math] is the relaxed length of the spring, when the spring is neither stretched nor compressed.

[math]\displaystyle{ L }[/math] is the length that the spring after it has been stretched or compressed.

[math]\displaystyle{ k_s }[/math] is the spring stiffness, which is a constant inherent to the property of the spring.

The spring force can also be modeled as a vector by the equation [math]\displaystyle{ \vec{F}_{spring} = -k_s s \hat{L} }[/math], where [math]\displaystyle{ \hat{L} }[/math] is the direction that the spring is stretched or compressed.

The constant of proportionality (k) is called the spring constant. The spring constant is a value unique to a particular string that represents its "stiffness". The spring constant is dependent on the amount of force required to stretch or compress the spring. A higher value of k corresponds to a greater force needed to stretch/compress the spring. The spring constant is most commonly represented with the unit newton per meter [N/m], but can sometimes be seen in newtons per centimeter [N/cm] or newtons per millimeter [N/mm].

spring with k = 5[1]

spring with k = 10[2]

The negative sign in the equation above gives the spring force its direction. If the spring is stretched in the positive direction (+x) the spring force pulls back in the negative direction (−F). If the spring is compressed in the negative direction (−x), the spring force pushes back in the positive direction (+F).

These models are linear models of the spring force and not the true force under every scenario. In a real system, the spring will deform when stretched and compressed, and thus change its spring constant; however, in a small enough stretches this deformation will be negligible and the linear representation will be reasonably accurate.

A Computational Model

A GlowScript model of a spring that prints out the spring force vector[3]

The spring force can be computed with a loop that updates the position of an object and an attached spring. Using a small enough time step, these quantities can be calculated to a reasonable degree of accuracy. The computational approach to spring force problems can be extremely useful, as the spring force is non-constant. For every change in position, which the spring force affects, the spring force changes. Because of this nature of the spring force, iterative calculations prove rather useful in its calculation. The code below demonstrates how knowing the value of the spring stiffness and relaxed length constants and keeping track of the spring position can be used to calculate and update the the spring force.

#GlowScript 1.1 VPython

L0 = 0.1 #the relaxed length of the spring
ks = 15 #spring constant

#plate holding spring end
plate= box(pos=vec(-.1,0,0), size=vec(.005,.1,.1))

# ball and spring objects
ball=sphere(pos=vec(-L0+.1,0,0), radius=0.02, color=color.red, make_trail=true)
spring=helix(pos=plate.pos, axis=ball.pos-plate.pos, radius=.02, coils=10)

ball.m = 0.1 #mass of the ball in kg
ball.p = ball.m * vec(0.5,0,0) #initial momentum

t = 0 #time
dt = 0.01 #size of the time step

#loops forever
while True: 
    rate(10) #100 calculations per second
    
    #length of the spring
    L = ball.pos - plate.pos
    
    #spring force
    Fs = -ks * (mag(L) - L0) * norm(L)
    
    #update the momentum of the ball
    ball.p = ball.p + Fs * dt
    
    #update the position of the ball
    ball.pos= ball.pos + ball.p * dt / ball.m
    
    #update the spring
    spring.axis = ball.pos - plate.pos

Accuracy

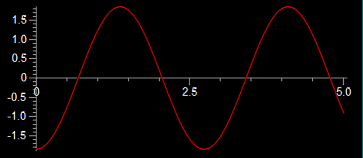
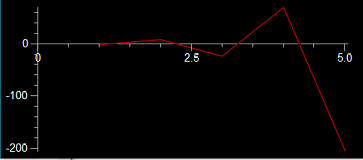
If we have a step-size of five seconds, we are assuming that force of the spring is constant for those five seconds. This simplifying assumption decreases the accuracy of our model. Hence, in order to improve the accuracy of the computational model, we can decrease the time step-size. The graphs below display the difference between using a .01 second step-size (left graph) and 1 second step-size (right graph).

Examples

Simple

Suppose a spring has been calibrated to have a spring stiffness of 300 N/m. You pull on the spring at rest and observe that it stretches a length of 0.02 m. What is the magnitude of the force exerted by the spring?

[math]\displaystyle{ \vert \vec{F}_{spring} \vert = k_s \vert s \vert }[/math]

[math]\displaystyle{ \vert \vec{F}_{spring} \vert = (300 N/m)(0.02m) }[/math]

[math]\displaystyle{ \vert \vec{F}_{spring} \vert = 6N }[/math]

Middling

Suppose a spring sits at the origin with a spring stiffness of 300 N/m. The spring has a relaxed length of 0.32 m. The spring has a 5 kg mass on the end at position <0.06, -0.41, 0> m. What is the current force exerted by the spring?

[math]\displaystyle{ \vec{F}_{spring} = -k_s s \hat{L} }[/math]

[math]\displaystyle{ \vec{L} = \langle 0.06, -0.41, 0 \rangle m - \langle0,0,0 \rangle m }[/math]

[math]\displaystyle{ \vert \vec{L} \vert = \sqrt{(0.06m)^2 + (-0.41m)^2} = 0.1717m }[/math]

[math]\displaystyle{ \hat{L} = \frac{ \langle 0.06,-0.41, 0 \rangle m}{0.1717 m} = \langle 0.35, -2.39, 0 \rangle m }[/math]

[math]\displaystyle{ s = 0.1717m - 0.32m = -0.1483m }[/math]

[math]\displaystyle{ \vec{F}_{spring} = -(300N/m)(-0.1483m) \langle 0.35, -2.39, 0 \rangle m = \langle 15.57, -106.33, 0 \rangle N }[/math]

Difficult

A spring sitting vertically on a table. The spring has a relaxed length of 0.3 m and a spring stiffness of 4 N/m. A 0.8 kg block is stuck atop the spring. You push the block and spring down so the bottom of the block is 0.1 m from the surface of the table. What is the net force acting upon the block at this moment?

[math]\displaystyle{ \vec{F}_{net} = \vec{F}_{Spring} + \vec{F}_{g} }[/math]

[math]\displaystyle{ \vec{F}_{spring} = -k_s s \hat{L} }[/math]

[math]\displaystyle{ \vec{L} = \langle 0, 0.1, 0 \rangle m - \langle0,0,0 \rangle m }[/math]

[math]\displaystyle{ \vert \vec{L} \vert = \sqrt{(0.1m)^2} = 0.1m }[/math]

[math]\displaystyle{ \hat{L} = \frac{ \langle 0,0.1, 0 \rangle m}{0.1 m} = \langle 0, 1, 0 \rangle m }[/math]

[math]\displaystyle{ s = 0.1m - 0.3m = -0.2m }[/math]

[math]\displaystyle{ \vec{F}_{spring} = -(4N/m)(-0.2m) \langle 0, 1, 0 \rangle m = \langle 0, 0.8, 0 \rangle N }[/math]

[math]\displaystyle{ \vec{F}_{g} = \langle 0, -mg, 0 \rangle = \langle 0, -(0.8kg)(9.81m/s^2), 0\rangle = \langle 0, -7.848, 0\rangle }[/math]

[math]\displaystyle{ \vec{F}_{net} = \langle 0, 0.8, 0 \rangle N + \langle 0, -7.848, 0\rangle N }[/math]

[math]\displaystyle{ \vec{F}_{net} = \langle 0, -7.048, 0 \rangle N }[/math]

Practical Applications

Elastic potential energy relates primarily to springs, but springs are a major part of everyday life. They can be found in everything from the shock-absorber assembly of a motor vehicle to the supports of a trampoline fabric, and in both cases, springs blunt the force of impact.

If one were to jump on a piece of trampoline fabric stretched across an ordinary table—one with no springs—the experience would not be much fun, because there would be little bounce. On the other hand, the elastic potential energy of the trampoline's springs ensures that anyone of normal weight who jumps on the trampoline is liable to bounce some distance into the air. As a person's body comes down onto the trampoline fabric, this stretches the fabric (itself highly elastic) and, hence, the springs. Pulled from a position of equilibrium, the springs acquire elastic potential energy, and this energy makes possible the upward bounce.

As a car goes over a bump, the spring in its shock-absorber assembly is compressed, but the elastic potential energy of the spring immediately forces it back to a position of equilibrium, thus ensuring that the bump is not felt throughout the entire vehicle. However, springs alone would make for a bouncy ride; hence, a modern vehicle also has shock absorbers. The shock absorber, a cylinder in which a piston pushes down on a quantity of oil, acts as a damper—that is, an inhibitor of the springs' oscillation.

Additionally, many objects in daily life oscillate in a spring-like way, yet people do not commonly associate them with springs. For example, a rubber band, which behaves very much like a spring, possesses high elastic potential energy. It will oscillate when stretched from a position of stable equilibrium.

Rubber is composed of long, thin molecules called polymers, which are arranged side by side. The chemical bonds between the atoms in a polymer are flexible and tend to rotate, producing kinks and loops along the length of the molecule that may not be visible to the naked eye. The very elastic polymers in rubber are called elastomers, and when a piece of rubber is pulled, the kinks and loops in the elastomers straighten.

The structure of rubber gives it a high degree of elastic potential energy, and in order to stretch rubber to maximum displacement, there is a powerful restoring force that must be overcome. This can be illustrated if a rubber band is attached to a ceiling, like the spring in the earlier example, and allowed to hang downward. If it is pulled down and released, it will behave quite similarly to a spring.

The oscillation of a rubber band will be even more appreciable if a weight is attached to the "free" end—that is, the end hanging downward. This is equivalent, on a small scale, to a bungee jumper attached to a cord. The type of cord used for bungee jumping is highly elastic; otherwise, the sport would be even more dangerous than it already is. Because of the cord's elasticity, when the bungee jumper appears to reach the end of his rope, he bounces back up and at a certain point begins to fall again, repeating the cycle over and over again until he reaches the point of stable equilibrium.

History

The concept of spring force was first discovered in 1660 by Robert Hooke. Hooke's linear model of spring force expressed the force of the spring using the equation [math]\displaystyle{ F = kx }[/math], relating force, [math]\displaystyle{ F }[/math] and displacement, [math]\displaystyle{ x }[/math], by some constant [math]\displaystyle{ k }[/math]. Hooke originally stated this law in Latin: "Ut tensio, sic vis," or “As the extension, so the force.” This insight would lead Hooke to devise plans for a watch with a balance spring, that would make pocket watches much more accurate.

References

Ruth W. Chabay, Bruce A. Sherwood (2011). Matter & Interactions. John Wiley & Sons, Inc. p. 64.
Hyper Physics[8]

--Arj (talk) 23:35, 5 December 2015 (EST)

Spring Force

Contents